当前位置:网站首页>[mathematical logic] equivalent calculus and reasoning calculus of propositional logic (propositional logic | equivalent calculus | principal conjunctive (disjunctive) paradigm | reasoning calculus)**
[mathematical logic] equivalent calculus and reasoning calculus of propositional logic (propositional logic | equivalent calculus | principal conjunctive (disjunctive) paradigm | reasoning calculus)**
2022-07-03 16:41:00 【Programmer community】
List of articles
- One 、 Basic concepts of propositional logic
- Two 、 Equivalent calculus
- 3、 ... and 、 The LORD takes ( Disjunction ) normal form
- Four 、 Reasoning and calculation
- 1、 Additional law
- 2、 The law of simplification
- 3、 Hypothetical reasoning
- 4、 Reject
- 5、 Disjunctive syllogism
- 6、 Hypothetical syllogism
- 7、 Equivalent syllogism
- 8、 constructive dilemma
Reference blog :
- 【 Mathematical logic 】 Propositions and conjunctions ( proposition | Proposition symbolization | Truth connectives | no | Syntaxis | Disjunction | Non truth connectives | implication | Equivalent )
- 【 Mathematical logic 】 Propositional logic ( Review of propositions and connectives | Propositional formula | Connective priority | Truth table Satisfiability Paradoxical Tautology )
- 【 Mathematical logic 】 Propositional logic ( Equivalent calculus | Idempotent law | Commutative law | Associative law | Distributive law | De Morgan law | absorptivity | Law of zero | The same thing | The law of excluded middle | Law of contradiction | Double negative rate | Implication equivalence … )
- 【 Mathematical logic 】 normal form ( Conjunctive paradigm | Disjunctive normal form | Major item | Small term | The maximal term | minterm | The main conjunctive paradigm | Principal disjunctive normal form | Equivalent calculus method for principal analysis / Conjunctive paradigm | Truth table method for principal analysis / Conjunctive paradigm )
- 【 Mathematical logic 】 Propositional logic ( Propositional logic inference | The formal structure of reasoning | The law of reasoning | Additional law | The law of simplification | Hypothetical reasoning | Reject | Disjunctive syllogism | Hypothetical syllogism | Equivalent syllogism | constructive dilemma )
- 【 Mathematical logic 】 Propositional logic ( Judgment of the correctness of propositional logic reasoning | The formal structure is forever true - Equivalent calculus | Deduce the conclusion from the premise - logical reasoning )
One 、 Basic concepts of propositional logic
Basic concepts of propositional logic
- Propositional logic connectives
- Truth table
- Propositional logic type : Satisfiability , Yongzhen style , Permanent falsehood ;
1 . Propositional formula form :
① Single Propositional argument / Propositional constant Is a proposition formula ;
② If
A
A
A Is a proposition formula , be
(
¬
A
)
(\lnot A)
(¬A) It is also a propositional formula ;
③ If
A
,
B
A,B
A,B Is a proposition formula , be
(
A
∧
B
)
,
(
A
∨
B
)
,
(
A
→
B
)
,
(
A
B
)
(A \land B) , (A \lor B), (A \to B), (A \leftrightarrow B)
(A∧B),(A∨B),(A→B),(AB) It is also a propositional formula ;
④ A limited number of times application ① ② ③ Formed symbol string Is a proposition formula ; ( Infinite times cannot )
2 . Conjunctions :
Atomic proposition :
p
,
q
,
r
p , q , r
p,q,r Express Atomic proposition , Also known as Simple proposition ;
- really :
1
1
1 Express Propositional truth value It's true ;
- false :
0
0
0 Express Propositional truth value For false ;
Conjunctions : Last blog 【 Mathematical logic 】 Predicate logic ( Individual words | Individual domain | The predicate | Full name quantifier | There are quantifiers | Predicate formula | exercises ) 3、 ... and . Conjunctions The chapter explains the connectives ;
- Negative connectives :
¬
\lnot
¬
- Conjunctions :
∧
\land
p
∧
q
p \land q
p∧q ,
p
q
pq
pq Tongzhen , The result is true , The rest is false ;
∧ ,
- Disjunctive connectives :
∨
\lor
p
∨
q
p \lor q
p∨q ,
p
q
pq
pq Same as , The result is false , The rest is true ;
∨ ,
- Implicative connectives :
→
\to
p
→
q
p \to q
p→q ,
p
p
p really
q
q
q false , The result is false , The rest is true ;
→ ,
- Equivalent connectives :
\leftrightarrow
p
q
p \leftrightarrow q
pq ,
p
q
pq
pq When the truth value is the same, it is true , Indicates equivalence ,
p
q
pq
pq If the true value is opposite, it is false , Equivalence does not hold ;
,
Connective priority :
“
¬
\lnot
¬” Greater than “
∧
,
∨
\land , \lor
∧,∨” Greater than “
→
,
\to, \leftrightarrow
→,”
∧
,
∨
\land , \lor
∧,∨ Same priority ;
→
,
\to, \leftrightarrow
→, Same priority ;
3 . Propositional logic type :
Satisfiability : Truth table , At least one result is true , It can be true ;
Paradoxical ( Permanent falsehood ) : All truth values are false ;
Satisfiability And Paradoxical , yes A choice Of , Compound proposition Or Satisfiability , Or Paradoxical ;
Tautology ( Yongzhen style ) Is a kind of satisfiable ;
4 . Simple proposition formalization :
Reference resources : Compound proposition And Proposition symbolization
Define propositions : Use
p
,
q
p,q
p,q A declarative sentence that stands for truth and falsehood ;
Use connectives : Then use connectives to connect these
p
,
q
p,q
p,q proposition ;
Reference blog :
- 【 Mathematical logic 】 Propositions and conjunctions ( proposition | Proposition symbolization | Truth connectives | no | Syntaxis | Disjunction | Non truth connectives | implication | Equivalent )
- 【 Mathematical logic 】 Propositional logic ( Review of propositions and connectives | Propositional formula | Connective priority | Truth table Satisfiability Paradoxical Tautology )
Two 、 Equivalent calculus
Equivalent concept :
A
,
B
A , B
A,B It's two propositional formulas , If
A
B
A \leftrightarrow B
AB It's Yongzhen style , that
A
,
B
A,B
A,B The two propositional formulas are equivalent , Remember to do
A
⇔
B
A \Leftrightarrow B
A⇔B ;
Equivalence calculus replacement rule :
A
A
A and
B
B
B Two propositional formulas , Sure Replace each other , Whenever there is
A
A
A All places can be replaced with
B
B
B , Whenever there is
B
B
B All places can be replaced with
A
A
A ;
Basic operation rules :
- 1. Idempotent law :
A
⇔
A
∨
A
A \Leftrightarrow A \lor A
A⇔A∨A ,
A
⇔
A
∧
A
A \Leftrightarrow A \land A
A⇔A∧A
- 2. Commutative law :
A
∨
B
⇔
B
∨
A
A \lor B \Leftrightarrow B \lor A
A∨B⇔B∨A ,
A
∧
B
⇔
B
∧
A
A \land B \Leftrightarrow B \land A
A∧B⇔B∧A
- 3. Associative law :
(
A
∨
B
)
∨
C
⇔
A
∨
(
B
∨
C
)
(A \lor B ) \lor C \Leftrightarrow A \lor (B \lor C)
(A∨B)∨C⇔A∨(B∨C) ,
(
A
∧
B
)
∧
C
⇔
A
∧
(
B
∧
C
)
(A \land B ) \land C \Leftrightarrow A \land (B \land C)
(A∧B)∧C⇔A∧(B∧C)
- 4. Distributive law :
A
∨
(
B
∧
C
)
⇔
(
A
∨
B
)
∧
(
A
∨
C
)
A \lor (B \land C) \Leftrightarrow ( A \lor B ) \land ( A \lor C )
A∨(B∧C)⇔(A∨B)∧(A∨C) ,
A
∧
(
B
∨
C
)
⇔
(
A
∧
B
)
∨
(
A
∧
C
)
A \land (B \lor C) \Leftrightarrow ( A \land B ) \lor ( A \land C )
A∧(B∨C)⇔(A∧B)∨(A∧C)
New operation rules :
- 5. De Morgan law :
¬
(
A
∨
B
)
⇔
¬
A
∧
¬
B
\lnot ( A \lor B ) \Leftrightarrow \lnot A \land \lnot B
¬(A∨B)⇔¬A∧¬B ,
¬
(
A
∧
B
)
⇔
¬
A
∨
¬
B
\lnot ( A \land B ) \Leftrightarrow \lnot A \lor \lnot B
- With And (
∧
\land
∧ ) Not (
¬
\lnot
¬ ) , I can represent or (
∨
\lor
∨ )
- With or (
∨
\lor
∨ ) Not (
¬
\lnot
¬ ) , I can represent And (
∧
\land
∧ )
¬(A∧B)⇔¬A∨¬B
- With And (
- 6. absorptivity :
- The former absorbs the latter :
A
∨
(
A
∧
B
)
⇔
A
A \lor ( A \land B ) \Leftrightarrow A
A∨(A∧B)⇔A
- The latter absorbs the former :
A
∧
(
A
∨
B
)
⇔
A
A \land ( A \lor B ) \Leftrightarrow A
A∧(A∨B)⇔A ;
- The former absorbs the latter :
0
,
1
0 , 1
0,1 Related operation laws :
- 7. Law of zero :
A
∨
1
⇔
1
A \lor 1 \Leftrightarrow 1
A∨1⇔1 ,
A
∧
0
⇔
0
A \land 0 \Leftrightarrow 0
1
1
1 Is or arithmetic zero yuan ,
0
0
0 It's with operation zero yuan ;
- And zero yuan The result of the operation is zero yuan ;
A∧0⇔0
- 8. The same thing :
A
∨
0
⇔
A
A \lor 0 \Leftrightarrow A
A∨0⇔A ,
A
∧
1
⇔
A
A \land 1 \Leftrightarrow A
0
0
0 Is or arithmetic Unit element ,
1
1
1 yes And arithmetic Unit element
- And Unit element The result of the operation is In itself
A∧1⇔A
- 9. The law of excluded middle :
A
∨
¬
A
⇔
1
A \lor \lnot A \Leftrightarrow 1
A∨¬A⇔1
- 10. Law of contradiction :
A
∧
¬
A
⇔
0
A \land \lnot A \Leftrightarrow 0
A∧¬A⇔0
The duality principle is applicable to the above operation law , Put both sides
∧
,
∨
\land , \lor
∧,∨ swap , meanwhile
0
,
1
0 ,1
0,1 swap , Equivalence still holds ;
Equivalent implication operation law :
- 11. Double negative rate :
¬
¬
A
⇔
A
\lnot \lnot A \Leftrightarrow A
¬¬A⇔A
- 12. Implication equivalence :
A
→
B
⇔
¬
A
∨
B
A \to B \Leftrightarrow \lnot A \lor B
- Replace implied connectives : Contains connectives
→
\to
→ It's not necessary , Use
¬
,
∨
\lnot , \lor
¬,∨ Two connectives can be substituted Contains connectives ;
A→B⇔¬A∨B
- Replace implied connectives : Contains connectives
- 13. Equivalent equation :
A
B
⇔
(
A
→
B
)
∨
(
B
→
A
)
A \leftrightarrow B \Leftrightarrow ( A \to B ) \lor ( B \to A )
- Double arrow ( Equivalent connectives ) It can be understood as a necessary condition for re division
A
→
B
A \to B
A→B ( Contains connectives ) Comprehend
A
A
A yes
B
B
B Sufficient conditions of ,
B
B
B yes
A
A
A Necessary conditions
B
→
A
B \to A
B→A ( Contains connectives ) Comprehend
B
B
B yes
A
A
A Sufficient conditions of ,
A
A
A yes
B
B
B Necessary conditions
- Replace equivalent connectives : Equivalent connectives
\leftrightarrow
It's not necessary , Use
→
,
∨
\to , \lor
→,∨ Two connectives can be substituted Equivalent connectives ;
AB⇔(A→B)∨(B→A)
- 14. Equivalent negative equivalent :
A
B
⇔
¬
A
¬
B
A \leftrightarrow B \Leftrightarrow \lnot A \leftrightarrow \lnot B
AB⇔¬A¬B
- 15. Hypothetical translocation ( Converse no proposition ) :
A
→
B
⇔
¬
B
→
¬
A
A \to B \Leftrightarrow \lnot B \to \lnot A
A
A
A be called The front part ,
B
B
B be called Afterpiece ( Conclusion ) ;
A→B⇔¬B→¬A
- 16. To fallacy ( Reduction to absurdity ) :
(
A
→
B
)
∧
(
A
→
¬
B
)
⇔
¬
A
( A \to B ) \land ( A \to \lnot B ) \Leftrightarrow \lnot A
- This is the principle of disproof , from
A
A
A Deduce
B
B
B and
¬
B
\lnot B
¬B ,
B
B
B and
¬
B
\lnot B
¬B Is contradictory , be
A
A
A It's wrong. ,
¬
A
\lnot A
¬A Yes. ;
(A→B)∧(A→¬B)⇔¬A
- This is the principle of disproof , from
Reference blog : 【 Mathematical logic 】 Propositional logic ( Equivalent calculus | Idempotent law | Commutative law | Associative law | Distributive law | De Morgan law | absorptivity | Law of zero | The same thing | The law of excluded middle | Law of contradiction | Double negative rate | Implication equivalence … )
3、 ... and 、 The LORD takes ( Disjunction ) normal form
1 . minterm
minterm : minterm yes A kind of Simple conjunction ;
- 1. Premise ( Simple conjunction ) : contain
n
n
n individual Propositional variables Of Simple conjunction ;
- 2. The number of occurrence of propositional variables : Each propositional variable all With written words Of form In which , And Only appears once ;
- 3. Where the propositional variable appears : The first
i
i
i (
1
≤
i
≤
n
1 \leq i \leq n
1≤i≤n ) Words appear in From the left The first
i
i
n
n
n It refers to the number of propositional variables ;
i A place ;
- 4. Summary of minor items : Meeting the above three conditions Simple conjunction , be called minterm ;
- 5.
m
i
m_i
mi And
M
i
M_i
¬
m
i
*
M
i
\lnot m_i \iff M_i
¬mi*Mi②
¬
M
i
*
m
i
\lnot M_i \iff m_i
¬Mi*mi
Mi The relationship between :①
Each proposition In the order specified , And Only once Of Simple conjunction , It is called the minimal term ;
Minima list the true assignment , Because only one case of conjunctive form comes true , That is Quanzhen ;
2 . The maximal term
About The maximal term Of explain :
- 1. The number of maximal terms :
n
n
n individual Propositional argument Meeting produce
2
n
2^n
2n individual The maximal term ;
- 2. Not equal to each other :
2
n
2^n
2n A very large item all Not equal to each other ;
- 3. The maximal term :
m
i
m_i
mi Express The first
i
i
i A very large item , among
i
i
i Is the largest item False assignment Of Decimal means ;
- 4. Maximum item name : The first
i
i
i A very large item , be called
M
i
M_i
Mi ;
- 5.
m
i
m_i
mi And
M
i
M_i
¬
m
i
*
M
i
\lnot m_i \iff M_i
¬mi*Mi②
¬
M
i
*
m
i
\lnot M_i \iff m_i
¬Mi*mi
Mi The relationship between :①
Each proposition In the order specified , And Only once Of Simple disjunctive , It is called the minimal term ;
The maximal term lists the false assignment , Because only one case of disjunction is false , That's all vacation ;
3 . The LORD takes ( Disjunction ) normal form
① List requirements The LORD takes ( Disjunction ) normal form Truth table of ;
p
,
q
,
r
p , q , r
p,q,r The truth value of three propositions starts from
0
,
0
,
0
0,0,0
0,0,0 To
1
,
1
,
1
1,1,1
1,1,1, Yes
2
3
=
8
2^3 = 8
23=8 Column , Each column corresponds to
m
0
∼
m
8
m_0 \sim m_8
m0∼m8 minterm ,
M
0
∼
M
8
M_0 \sim M_8
M0∼M8 The maximal term ;
② Principal disjunctive normal form ( Take the minimum ) : The truth value in the truth table is
1
1
1 The column of take minterm ; minterm True assignment ; According to the subscript and true assignment of the minimum term, the propositional formula of the minimum term can be listed ;
③ The main conjunctive paradigm ( Take the maximum ) : The truth value in the truth table is
0
0
0 The column of take The maximal term ; The maximal term False assignment ; According to the subscript of the maximum term and the false assignment, the propositional formula of the maximum term can be listed
4 . summary :
minterm : Combined type , True assignment , Take the truth table when calculating really Column ;
The maximal term : disjunction , False assignment , Take the truth table when calculating false Column ;
Reference blog : 【 Mathematical logic 】 normal form ( Conjunctive paradigm | Disjunctive normal form | Major item | Small term | The maximal term | minterm | The main conjunctive paradigm | Principal disjunctive normal form | Equivalent calculus method for principal analysis / Conjunctive paradigm | Truth table method for principal analysis / Conjunctive paradigm )
Four 、 Reasoning and calculation
The formal structure of reasoning
Premise :
A
1
,
A
2
,
⋯
,
A
k
A_1 , A_2 , \cdots , A_k
A1,A2,⋯,Ak
Conclusion :
B
B
B
The formal structure of reasoning is :
(
A
1
∧
A
2
∧
⋯
∧
A
k
)
→
B
(A_1 \land A_2 \land \cdots \land A_k) \to B
(A1∧A2∧⋯∧Ak)→B
The law of reasoning :
A
,
B
A,B
A,B There are two propositions , If
A
→
B
A \to B
A→B It's Yongzhen style , that
A
⇒
B
A \Rightarrow B
A⇒B ;
1、 Additional law
Additional law :
A
⇒
(
A
∨
B
)
A \Rightarrow (A \lor B)
A⇒(A∨B)
according to The law of reasoning ,
A
→
(
A
∨
B
)
A \to (A \lor B)
A→(A∨B) Implicative form yes Yongzhen style ;
Premise :
A
A
A
Conclusion :
A
∨
B
A \lor B
A∨B
A
A
A Yes. , that
A
∨
B
A \lor B
A∨B That's right. , The latter is an addition to the former
B
B
B ;
2、 The law of simplification
The law of simplification :
(
A
∧
B
)
⇒
A
( A \land B ) \Rightarrow A
(A∧B)⇒A ,
(
A
∧
B
)
⇒
B
( A \land B ) \Rightarrow B
(A∧B)⇒B
according to The law of reasoning ,
(
A
∧
B
)
→
A
( A \land B ) \to A
(A∧B)→A ,
(
A
∧
B
)
→
B
( A \land B ) \to B
(A∧B)→B Implicative form yes Yongzhen style ;
Premise :
A
∧
B
A \land B
A∧B
Conclusion :
A
A
A or
B
B
B
A
∧
B
A \land B
A∧B Yes. , that
A
A
A or
B
B
B That's right. , The latter is simplified on the basis of the former ;
3、 Hypothetical reasoning
Hypothetical reasoning :
(
A
→
B
)
∧
A
⇒
B
( A \to B ) \land A \Rightarrow B
(A→B)∧A⇒B
according to The law of reasoning ,
(
A
→
B
)
∧
A
→
B
( A \to B ) \land A \to B
(A→B)∧A→B Implicative form yes Yongzhen style ;
Premise :
A
→
B
A \to B
A→B ,
A
A
A
Conclusion :
B
B
B
This is a typical small three paragraph theory ;
4、 Reject
Reject :
(
A
→
B
)
∧
¬
B
⇒
¬
A
( A \to B ) \land \lnot B \Rightarrow \lnot A
(A→B)∧¬B⇒¬A
according to The law of reasoning ,
(
A
→
B
)
∧
¬
B
→
¬
A
( A \to B ) \land \lnot B \to \lnot A
(A→B)∧¬B→¬A Implicative form yes Yongzhen style ;
Premise :
A
→
B
A \to B
A→B ,
¬
B
\lnot B
¬B
Conclusion :
¬
A
\lnot A
¬A
It can be understood as a counter evidence ;
5、 Disjunctive syllogism
Disjunctive syllogism :
(
A
∨
B
)
∧
¬
A
⇒
B
( A \lor B ) \land \lnot A \Rightarrow B
(A∨B)∧¬A⇒B ,
(
A
∨
B
)
∧
¬
B
⇒
A
( A \lor B ) \land \lnot B \Rightarrow A
(A∨B)∧¬B⇒A
according to The law of reasoning ,
(
A
∨
B
)
∧
¬
A
→
B
( A \lor B ) \land \lnot A \to B
(A∨B)∧¬A→B ,
(
A
∨
B
)
∧
¬
B
→
A
( A \lor B ) \land \lnot B \to A
(A∨B)∧¬B→A Implicative form yes Yongzhen style ;
Premise :
A
∨
B
A \lor B
A∨B ,
¬
A
\lnot A
¬A
Conclusion :
B
B
B
(
A
∨
B
)
(A \lor B)
(A∨B) That's right. , among
A
A
A It's wrong. , that
B
B
B It must be right ;
(
A
∨
B
)
(A \lor B)
(A∨B) That's right. , among
B
B
B It's wrong. , that
A
A
A It must be right ;
Police often use reasoning methods to solve cases , Exclude suspects one by one ;
6、 Hypothetical syllogism
Hypothetical syllogism :
(
A
→
B
)
∧
(
B
→
C
)
⇒
(
A
→
C
)
( A \to B ) \land ( B \to C ) \Rightarrow ( A \to C )
(A→B)∧(B→C)⇒(A→C)
according to The law of reasoning ,
(
A
→
B
)
∧
(
B
→
C
)
→
(
A
→
C
)
( A \to B ) \land ( B \to C ) \to ( A \to C )
(A→B)∧(B→C)→(A→C) Implicative form yes Yongzhen style ;
Premise :
A
→
B
A \to B
A→B ,
B
→
C
B \to C
B→C
Conclusion :
A
→
C
A \to C
A→C
7、 Equivalent syllogism
Equivalent syllogism :
(
A
B
)
∧
(
B
C
)
⇒
(
A
C
)
( A \leftrightarrow B ) \land ( B \leftrightarrow C ) \Rightarrow ( A \leftrightarrow C )
(AB)∧(BC)⇒(AC)
according to The law of reasoning ,
(
(
A
B
)
∧
(
B
C
)
)
→
(
A
C
)
( ( A \leftrightarrow B ) \land ( B \leftrightarrow C ) ) \to ( A \leftrightarrow C )
((AB)∧(BC))→(AC) Implicative form yes Yongzhen style ;
Premise :
A
B
A \leftrightarrow B
AB ,
B
C
B \leftrightarrow C
BC
Conclusion :
A
C
A \leftrightarrow C
AC
8、 constructive dilemma
Equivalent syllogism :
(
A
→
B
)
∧
(
C
→
D
)
∧
(
A
∨
C
)
⇒
(
B
∨
D
)
( A \to B ) \land ( C \to D ) \land ( A \lor C ) \Rightarrow ( B \lor D )
(A→B)∧(C→D)∧(A∨C)⇒(B∨D)
according to The law of reasoning ,
(
(
A
→
B
)
∧
(
C
→
D
)
∧
(
A
∨
C
)
)
→
(
(
B
∨
D
)
)
( ( A \to B ) \land ( C \to D ) \land ( A \lor C ) ) \to ( ( B \lor D ) )
((A→B)∧(C→D)∧(A∨C))→((B∨D)) Implicative form yes Yongzhen style ;
Premise :
A
→
B
A \to B
A→B ,
C
→
D
C \to D
C→D ,
A
∨
C
A \lor C
A∨C
Conclusion :
B
∨
D
B \lor D
B∨D
Way of understanding :
A
A
A Is to develop the economy ,
B
B
B It's pollution
C
C
C Is not to develop the economy ,
D
D
D It's poverty
A
∨
B
A \lor B
A∨B Or develop the economy , Or do not develop the economy
The result is
B
∨
D
B \lor D
B∨D , Or produce pollution , Or endure poverty
Reference blog : 【 Mathematical logic 】 Propositional logic ( Propositional logic inference | The formal structure of reasoning | The law of reasoning | Additional law | The law of simplification | Hypothetical reasoning | Reject | Disjunctive syllogism | Hypothetical syllogism | Equivalent syllogism | constructive dilemma )
边栏推荐
- Mongodb installation and basic operation
- 什么是质押池,如何进行质押呢?
- Informatics Olympiad all in one YBT 1175: divide by 13 | openjudge noi 1.13 27: divide by 13
- Cocos Creator 2.x 自动打包(构建 + 编译)
- What is the maximum number of concurrent TCP connections for a server? 65535?
- Aike AI frontier promotion (7.3)
- Unity项目优化案例一
- 关于视觉SLAM的最先进技术的调查-A survey of state-of-the-art on visual SLAM
- CC2530 common registers for watchdog
- 深入理解 SQL 中的 Grouping Sets 语句
猜你喜欢
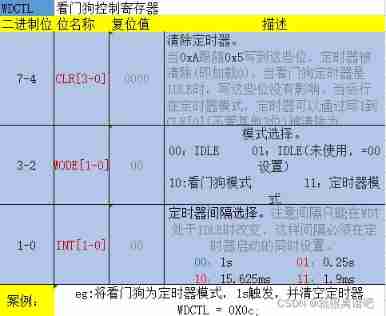
CC2530 common registers for watchdog
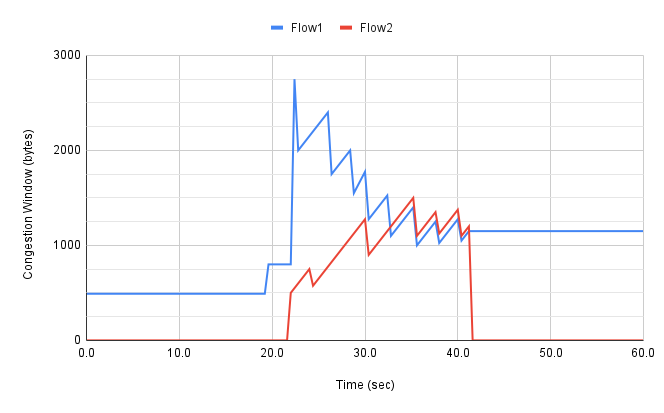
TCP擁塞控制詳解 | 3. 設計空間
一台服务器最大并发 tcp 连接数多少?65535?

Thread pool executes scheduled tasks

Netease UI automation test exploration: airtest+poco

Détails du contrôle de la congestion TCP | 3. Espace de conception

What material is sa537cl2 equivalent to in China? Sa537cl2 corresponding material

What material is 13crmo4-5 equivalent to in China? 13crmo4-5 chemical composition 13crmo4-5 mechanical properties

Interviewer: how does the JVM allocate and recycle off heap memory

arduino-esp32:LVGL项目(一)整体框架
随机推荐
Learn from me about the enterprise flutter project: simplified framework demo reference
Zebras are recognized as dogs, and Stanford found the reason why AI made mistakes
Everyone in remote office works together to realize cooperative editing of materials and development of documents | community essay solicitation
PHP production website active push (website)
中南大学|通过探索理解: 发现具有深度强化学习的可解释特征
(Supplement) double pointer topic
8 tips for effective performance evaluation
Hong Kong Polytechnic University | data efficient reinforcement learning and adaptive optimal perimeter control of network traffic dynamics
Google Earth engine (GEE) - daymet v4: daily surface weather data set (1000m resolution) including data acquisition methods for each day
Two sides of the evening: tell me about the bloom filter and cuckoo filter? Application scenario? I'm confused..
TCP congestion control details | 3 design space
NSQ源码安装运行过程
Acwing game 58
Pytorch 1.12 was released, officially supporting Apple M1 chip GPU acceleration and repairing many bugs
What material is sa537cl2? Analysis of mechanical properties of American standard container plate
14 topics for performance interviews between superiors and subordinates (4)
Unity项目优化案例一
AcWing 第58 场周赛
Interviewer: how does the JVM allocate and recycle off heap memory
[combinatorics] polynomial theorem (polynomial coefficients | full arrangement of multiple sets | number of schemes corresponding to the ball sub model | polynomial coefficient correlation identity)