Quick sequencing and optimization

Quick sort

Select one element from the currently considered array at a time , Try to move this element to the position where it should be arranged , such as 4 This element , It has a property 4 The previous elements are smaller than it , Later elements are larger than it , After that, we need to do something about less than 4 And greater than 4 The array of continues to use the idea of quick sorting , Gradually recurse down to complete the whole sorting process .

For quick sort, the process of moving the selected elements to the correct position is also the core of quick sort , In this process, we usually choose the first element of the array as the marker of our boundary , We record this point as l , Then we gradually traverse all the elements on the right that have not been accessed , In the process of traversal, we gradually sort out a part that is less than v Of this element , Part of it is greater than v Of this element , When let's have a record, it's less than v And greater than v The dividing point of , This point is j , The currently accessed element record is i.

How can we decide how the current element changes to maintain its current nature , If the current element e It's better than v Even bigger , Then he put it directly on the greater than v Part of the back .

Then consider the next element .

If the current element e It's better than v And smaller .

We only need the current orange part, that is j The last element of the position referred to and the element currently being investigated i Exchange .

After that, let's do some location maintenance ++j,++i.

And so on , The whole array is divided into three parts , The first element is v, The orange part is smaller than v, The purple part is larger than v.

The last thing we need to do is put the array l This position and array j Exchange this position , In this way, the whole array forms what we imagine , The front is smaller than v, Rear greater than v.

Optimize

• For small arrays , Optimize with insert sort ;
• Random in arr[l…r] In the range of , Select a value as the calibration point pivot. The subtree divided in the recursive process of quick sort cannot guarantee that the whole array is divided into two equally every time , In other words, the sub array may be one large and one small .
• 
• If the array is almost or completely ordered, then ：
• 

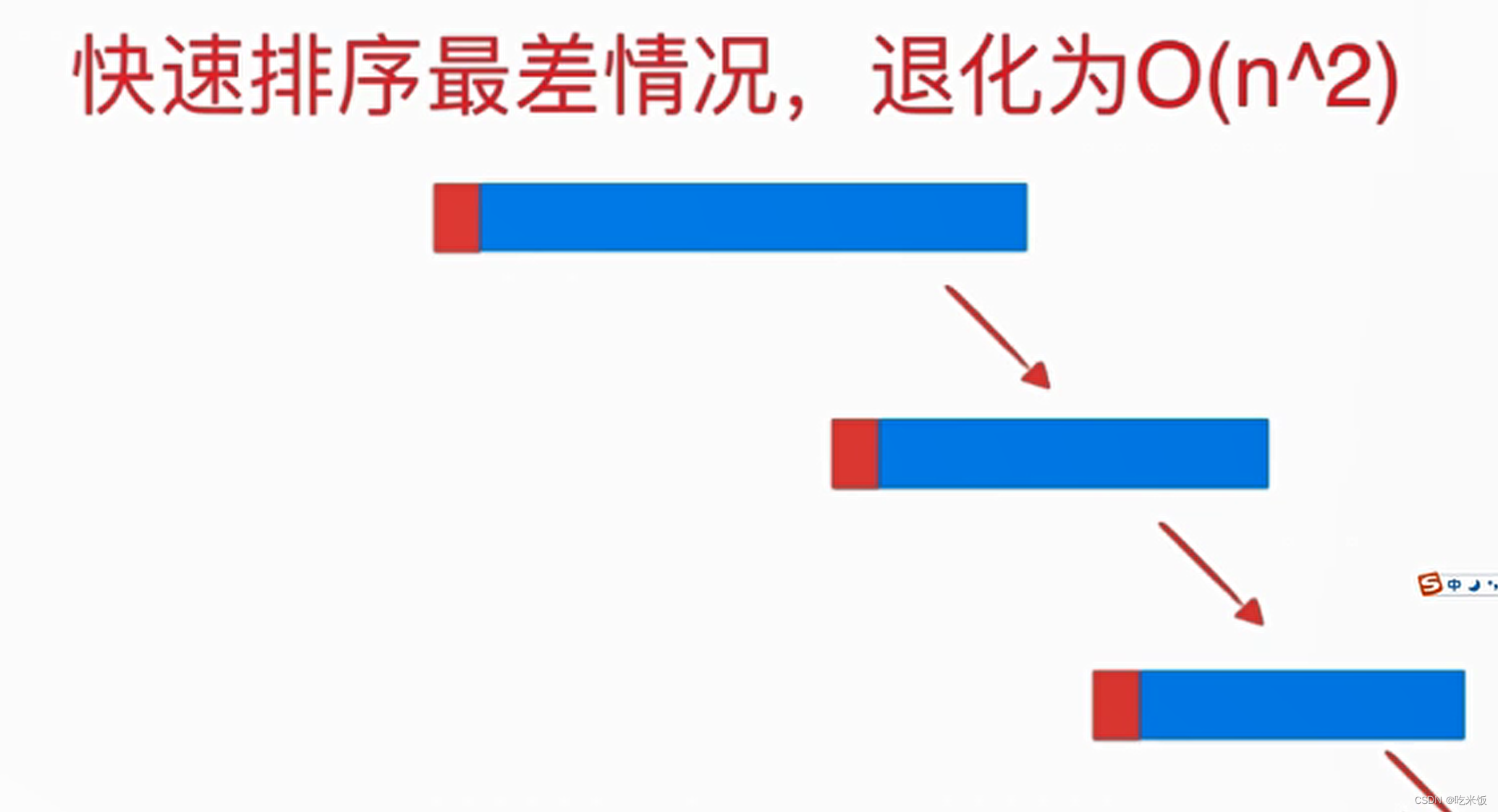
quickSort

//  Yes arr[l...r] Range array for insertion sort 
template<typename T>
void insertionSort(T arr[], int l, int r) {
    
   for (int i = l + 1; i <= r; ++i) {
    
       T e = arr[i];
       int j;
       for (j = i; j > l && arr[j - 1] > e; --j) {
    
           arr[j] = arr[j - 1];
       }
       arr[j] = e;
   }
}

//  Yes arr[l...r] In part partition operation 
//  return p,  bring arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template<typename T>
int __partition1(T arr[], const int l, const int r) {
    
   //  Optimize ： Random in arr[l...r] In the range of ,  Select a value as the calibration point pivot
   std::swap(arr[l], arr[rand() % (r - l + 1) + l]);
   const T v = arr[l];
   int j = l;
   // arr[l+1...j] < v ; arr[j+1...i) > v
   for (int i = l + 1; i <= r; ++i) {
    
       if (arr[i] < v) {
    
           std::swap(arr[++j], arr[i]);
       }
   }
   std::swap(arr[l], arr[j]);
   return j;
}
//  Yes arr[l...r] Quick sort the parts 
template<typename T>
void __quickSort(T arr[], const int l, const int r) {
    
   //  Optimize ： For small arrays ,  Optimize with insert sort 
   if (r - l <= 15) {
    
       insertionSort(arr, l, r);
       return;
   }
   const int p = __partition1(arr, l, r);
   __quickSort(arr, l, p - 1);
   __quickSort(arr, p + 1, r);
}

// Quick sort 
template<typename T>
void quickSort(T arr[], const int n) {
    
   srand(time(NULL));
   __quickSort(arr, 0, n - 1);
} 

Two way quick sort

In the previous quick sort, we didn't discuss equal v The situation of , Here, whether you put the equals on the left or the right , If there are a lot of duplicate elements in the whole array , Then it will cause extreme imbalance between the left and right arrays, so that the algorithm degenerates into O(n^2).

Now we will be less than v And greater than v At both ends of the array . First we start with i This position starts scanning backwards , When the element we face is still less than v When we continue to scan backwards , Know that we have encountered elements e, It is greater than or equal to v Of .

Again j The same is true ,

In this way, the two green parts are merged into orange and purple respectively .

and i and j Just exchange the positions of these two elements .

Then maintain the position ++i,–j, And so on .

quickSort2Ways

//  Yes arr[l...r] Range array for insertion sort 
template<typename T>
void insertionSort(T arr[], int l, int r) {
    
   for (int i = l + 1; i <= r; ++i) {
    
       T e = arr[i];
       int j;
       for (j = i; j > l && arr[j - 1] > e; --j) {
    
           arr[j] = arr[j - 1];
       }
       arr[j] = e;
   }
}

//  Two way quick sort partition
//  return p,  bring arr[l...p-1] <= arr[p] ; arr[p+1...r] >= arr[p]
//  The element of two-way fast row processing is exactly equal to arr[p] Pay attention to , See note below ：）
template<typename T>
int __partition2(T arr[], int l, int r) {
    
   //  Random in arr[l...r] In the range of ,  Select a value as the calibration point pivot
   std::swap(arr[l], arr[rand() % (r - l + 1) + l]);
   const T v = arr[l];
   // arr[l+1...i) <= v; arr(j...r] >= v
   int i = l + 1, j = r;
   while (true) {
    
       //  Pay attention to the boundary here , arr[i] < v,  It can't be arr[i] <= v
       //  Think about why ?
       while (i <= r && arr[i] < v)++i;
       //  Pay attention to the boundary here , arr[j] > v,  It can't be arr[j] >= v
       //  Think about why ?
       while (j >= l + 1 && arr[j] > v)--j;
       if (i > j)break;
       std::swap(arr[i], arr[j]);
       //arr[i] < v.  In the case of many consecutive same numbers ,i Move backward only once , meanwhile j Move forward at least once , Relative balance .
       //arr[i] <= vb,  In the case of many consecutive same numbers , i First, keep moving backwards , Until the conditions are met , Cause imbalance .
       ++i;
       --j;
   }
   std::swap(arr[l], arr[j]);
   return j;
}

//  Yes arr[l...r] Quick sort the parts 
template<typename T>
void __quickSort2Ways(T arr[], const int l, const int r) {
    
   //  For small arrays ,  Optimize with insert sort 
   if (r - l <= 15) {
    
       insertionSort(arr, l, r);
       return;
   }
   const int p = __partition2(arr, l, r);
   __quickSort2Ways(arr, l, p - 1);
   __quickSort2Ways(arr, p + 1, r);
}

// Quick sort 
template<typename T>
void quickSort2Ways(T arr[], const int n) {
    
   srand(time(NULL));
   __quickSort2Ways(arr, 0, n - 1);
}

Three way quick sorting

The previous idea of quick sorting is less than v Greater than v, The idea of three-way quick sorting is less than v be equal to v Greater than v. After such segmentation, in the process of recursion , For equal to v We don't care at all , Only recursion less than v Greater than v Do the same quick sort for the parts of .

Now we have to deal with i The element of position e, If the current element e It's exactly the same as v, So the element e Directly include green is equal to v Part of , Corresponding ++i, Let's deal with the next element .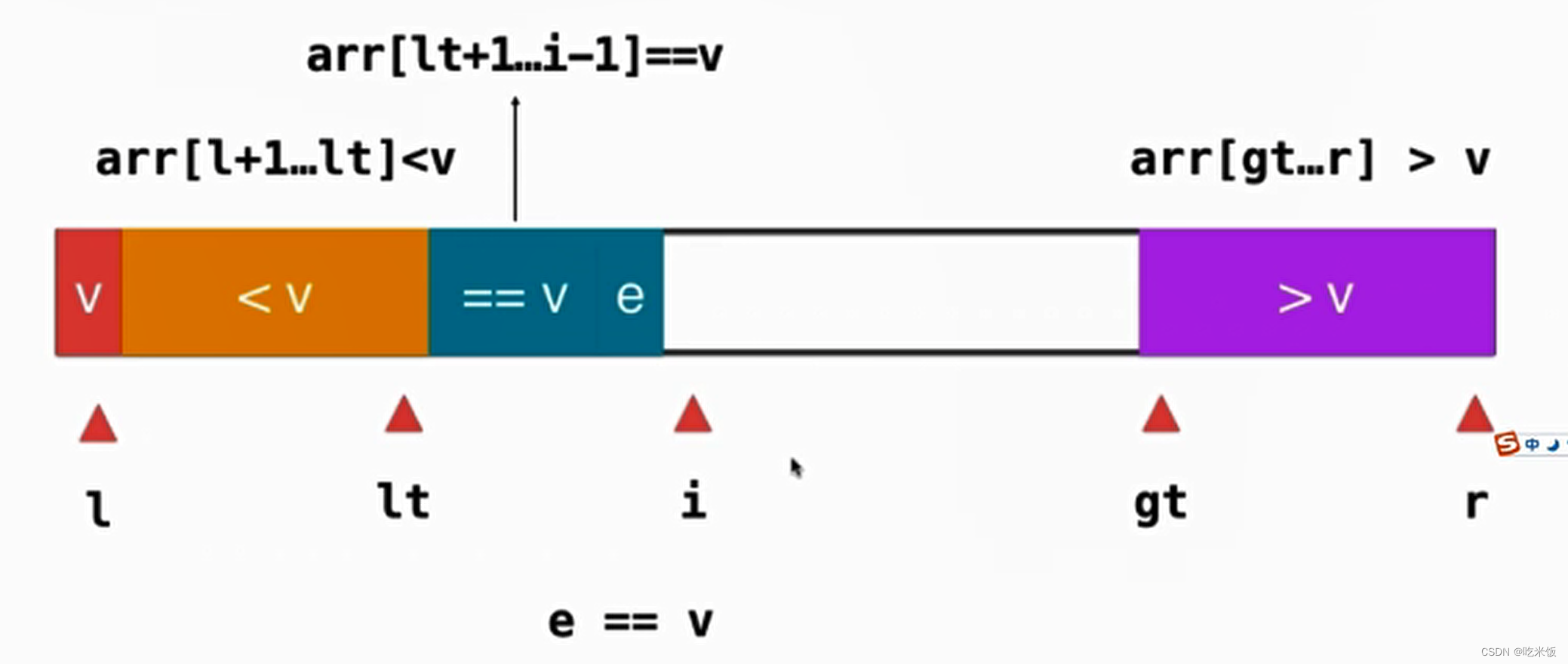

If the current element e Less than v, We just need to sum this element up to v Just exchange the first element of the part once .

After that, we should maintain the position ,++i,++lt, To see the next element .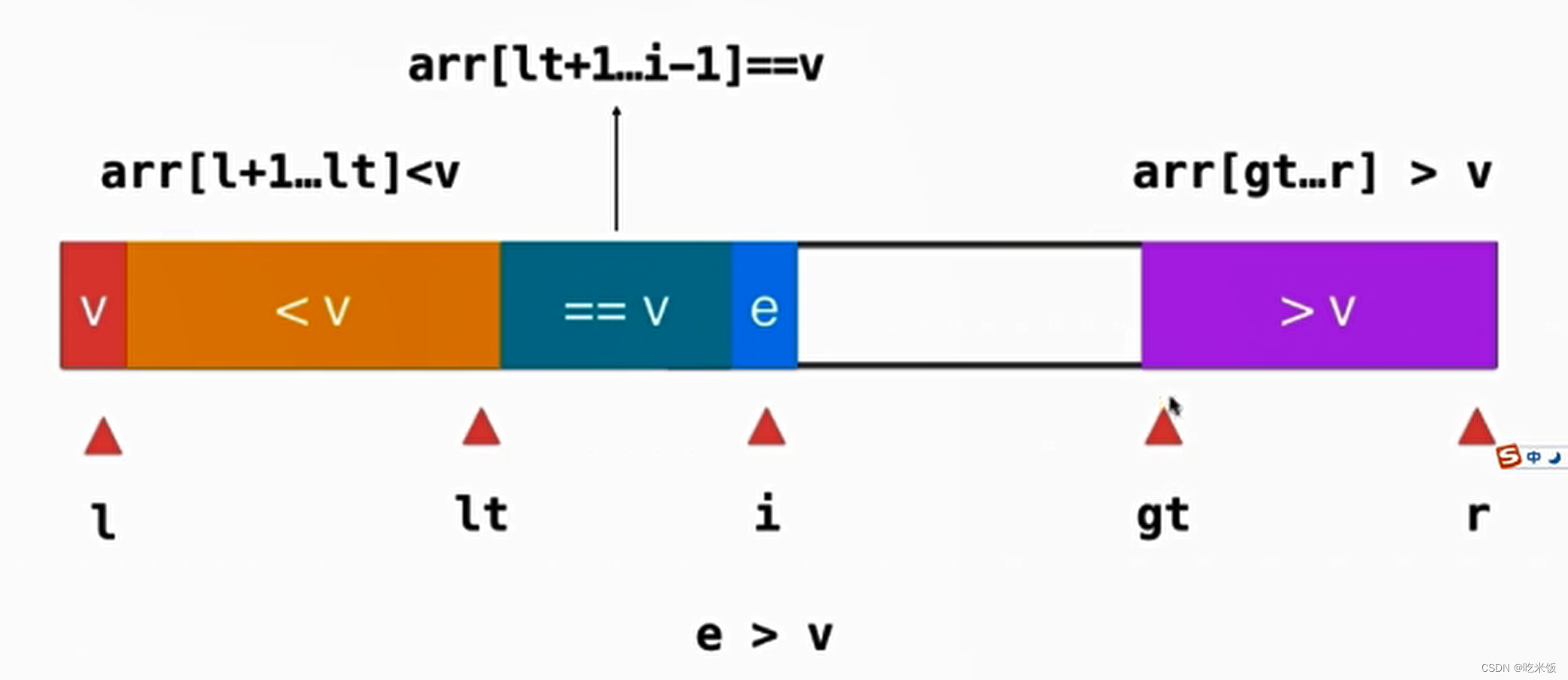

If the current element e Greater than v, We just need to combine this element with gt-1 Just exchange the elements of position once .

Accordingly, we should maintain gt The location of –gt, It should be noted that i We don't need to touch it , Because the position element exchanged with it has not been discussed .

And so on , Finally, we need l and lt The elements of position exchange positions .

At this point, our entire array becomes like this , After that, we just need to check the value of less than v The sum of parts is greater than v It's good to recursively sort the parts of , As for equal to v It has been placed in the appropriate position of the array .

quickSort3Ways

//  Yes arr[l...r] Range array for insertion sort 
template<typename T>
void insertionSort(T arr[], int l, int r) {
    
   for (int i = l + 1; i <= r; ++i) {
    
       T e = arr[i];
       int j;
       for (j = i; j > l && arr[j - 1] > e; --j) {
    
           arr[j] = arr[j - 1];
       }
       arr[j] = e;
   }
}

//  Recursive three-way quick sorting algorithm 
template<typename T>
void __quickSort3Ways(T arr[], const int l, const int r) {
    
   //  For small arrays ,  Optimize with insert sort 
   if (r - l <= 15) {
    
       insertionSort(arr, l, r);
       return;
   }

   //  Random in arr[l...r] In the range of ,  Select a value as the calibration point pivot
   std::swap(arr[l], arr[rand() % (r - l + 1) + l]);

   T v = arr[l];

   int lt = l;     // arr[l+1...lt] < v
   int gt = r + 1; // arr[gt...r] > v
   int i = l + 1;    // arr[lt+1...i) == v
   while (i < gt) {
    
       if (arr[i] < v) {
    
           std::swap(arr[i], arr[lt + 1]);
           ++i;
           ++lt;
       } else if (arr[i] > v) {
    
           std::swap(arr[i], arr[gt - 1]);
           --gt;
       } else {
     // arr[i] == v
           ++i;
       }
   }
   std::swap(arr[l], arr[lt]);
   __quickSort3Ways(arr, l, lt - 1);
   __quickSort3Ways(arr, gt, r);
}

//  For arrays that contain a lot of duplicate data ,  Three way fast platoon has great advantages 
template<typename T>
void quickSort3Ways(T arr[], const int n) {
    
   srand(time(nullptr));
   __quickSort3Ways(arr, 0, n - 1);
}

summary