Animation curves are used every day. Can you make one by yourself? After reading this article, you will!

Preface

Recently, I'm writing a chapter related to animation , Often used  

Curve

  This animation curve class , How exactly does this class implement ？ If you want to have a custom animation curve, how to do it ？ In this article, let's find out .

Curve  Class definition

View source code , 

Curve

  Class is defined as follows ：

abstract class Curve extends ParametricCurve<double> {
 const Curve();

 @override
 double transform(double t) {
 if (t == 0.0 || t == 1.0) {
 return t;
 }
 return super.transform(t);
 }
 
 Curve get flipped => FlippedCurve(this);
}


It doesn't seem to define anything ,  In fact, there are only two processes here , One is that the explicit data type is  

double

, The other is right  

transform

  Overloaded , It's just for parameters  t  Special treatment , Guarantee parameters  t  The scope of 0-1 Between , And the starting point value 0.0 And the end value 1.0 Not converted by the conversion function . Mainly defined in the upper layer

ParametricCurve

. Documentation is a suggested subclass overload

transformInternal

Method , Then let's keep looking up

ParametricCurve

The implementation of this class , The code is as follows ：

abstract class ParametricCurve<T> {
 const ParametricCurve();

 T transform(double t) {
 assert(t != null);
 assert(t >= 0.0 && t <= 1.0, 'parametric value $t is outside of [0, 1] range.');
 return transformInternal(t);
 }

 @protected
 T transformInternal(double t) {
 throw UnimplementedError();
 }

 @override
 String toString() => objectRuntimeType(this, 'ParametricCurve');
}


You can see , actually  

transform

  In addition to verifying the validity of parameters , It's actually called

transformInternal

Method , Therefore, subclasses must implement the method , Otherwise it will throw

UnimplementedError

abnormal .

Instance analysis

The source code above can be seen , The key is the parameters  

t

. This parameter  

t

  What does it stand for ？ The note says ：

Returns the value of the curve at point 

t

. —  return  t  The value corresponding to the curve of the point .

therefore  

t

  It can be considered as the abscissa of the curve , In order to ensure the consistency of the curve , Normalized , That is to say

t

All values are in 0-1 Between . That may be a little abstract , Let's see 2 Let's compare it with an example , First look at the simplest

 Curves.linear

  The implementation of the .

class _Linear extends Curve {
 const _Linear._();

 @override
 double transformInternal(double t) => t;
}


It's super simple , Go straight back to  t, In fact, the function corresponding to our mathematics is ：

y = f(t) = t


The corresponding curve is a slash . That is, within the set animation time , Will complete from 0-1 Linear transformation of , That is, the change is uniform . Linearity is easy to understand , Let's look at a deceleration curve

decelerate

The implementation of the .

class _DecelerateCurve extends Curve {
 const _DecelerateCurve._();

 @override
 double transformInternal(double t) {
 t = 1.0 - t;
 return 1.0 - t * t;
 }
}


Let's take a look first _DecelerateCurve  What is the calculation expression of .

Recall the uniform deceleration motion of our high school physics , The acceleration is negative （ Namely deceleration ） Distance calculation formula ：

The above deceleration curve can actually be regarded as the initial speed is 2, Acceleration is also 2 Decelerating motion of . Why if 2 What about this value , This is because  t  The range of phi is zero 0-1, The value range of the calculated result is still 0-1. You're sure to ask ,

Why should we ensure that the calculation result of the curve is 0-1

？

Let's assume that the calculation result is not 0-1 What will happen , For example, we want to move a component on the screen as 60 Pixels . Assume that the initial value of the animation curve is not 0. That means the initial moving distance is jumping . alike , If the end value is not 1.0, It means that the distance value at the last point is not 60.0, Then it means that you need to jump from the last point to the final 60 Pixel position （ Animation needs to ensure that the final moving distance is 60 Pixels ） This means that the animation will jump , If you draw a curve, it will look like the bottom （ Green is normal , The red line is abnormal ）.

This kind of animation experience is very bad ！ therefore , This is a key point , If your custom curve  

transformInternal

  The return value range of the method is not 0-1, It means that the animation will jump , The feeling of missing frames in the animation .

With this foundation , We can explain the basic mechanism of animation curve , In fact, at a given animation time （

Duration

） Within the scope of , Complete the transition from the initial state to the end state of the component , This shift is along the set  

Curve

  Class , And its abscissa is 0-1.0, The initial and end values of the curve are 0 and 1.0, As for the intermediate value, it can be lower than 0 Or exceed 1 Of . We can imagine that we move along a set curve , In the end, we will reach the set destination anyway , As for how to go , How many turns , How the speed changes is controlled by the curve . however , If the initial value of your curve is not 0 Or the end value is not 1, It's like jumping off a cliff ！

Sinusoidal animation curve

Let's have a sine curve animation to verify the above statement .

class SineCurve extends Curve {
 final int count;
 const SineCurve({this.count = 1}) : assert(count > 0);

 @override
 double transformInternal(double t) {
 return sin(2 * count* pi * t);
 }
}


count

  Parameters are used to control the cycle , That is, you can go back and forth a few more times before reaching your destination . Here we find , The initial value is 0, But a cycle （2π） The end value is also 0, In this way, a jump result will appear before the end of the animation . Let's look at the sample code , This example is to make the circle move down 60 Pixels .

AnimatedContainer(
 decoration: BoxDecoration(
 color: Colors.blue,
 borderRadius: BorderRadius.circular(30.0),
 ),
 transform: Matrix4.identity()..translate(0.0, up ? 60.0 : 0.0, 0.0),
 duration: Duration(milliseconds: 3000),
 curve: SineCurve(count: 1),
 child: ClipOval(
 child: Container(
 width: 60.0,
 height: 60.0,
 color: Colors.blue,
 ),
 ),
)


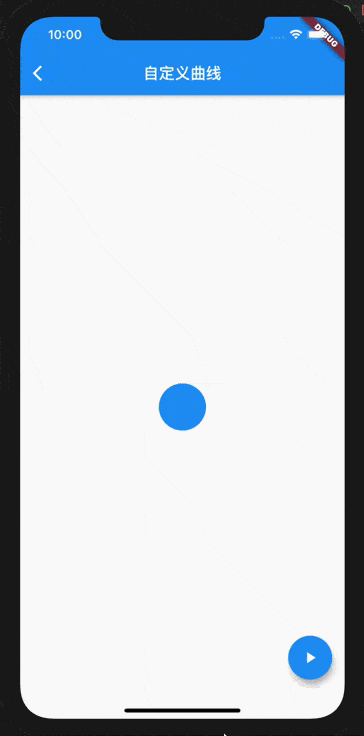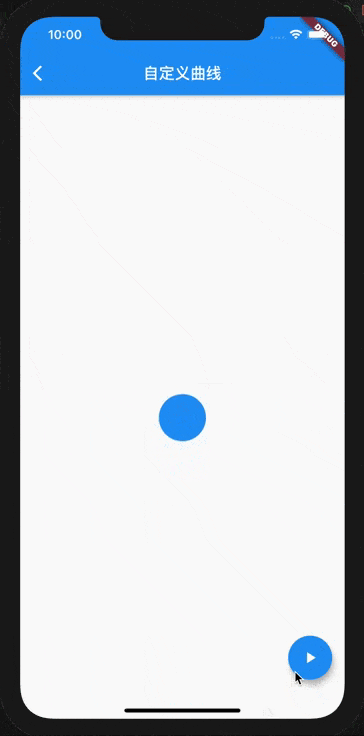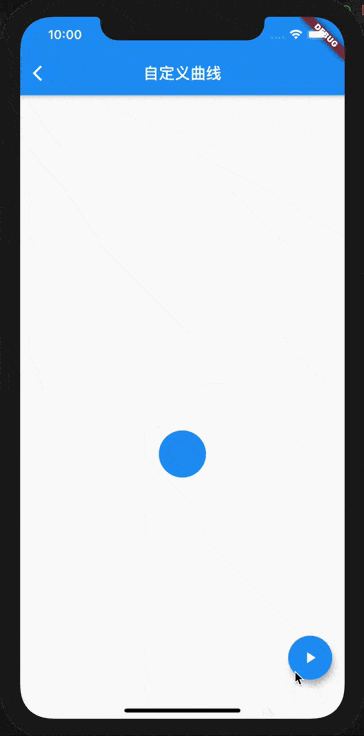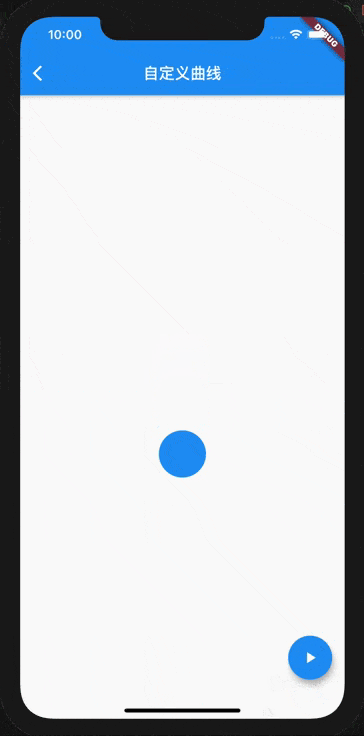
The operation effect is as follows , Look at the last frame from 0 Jump directly to 60 The location of .

How to adjust this , Let's look at what a sine curve looks like .

If we want to meet 0-1 Scope requirements , Then move back 90 Degree can reach . however , There's another problem , This destroys the periodicity , Setting up  

count=2

The result was wrong again . Let's look at the law , In fact, only the first cycle needs more movement 90 degree （ The point pointed by the arrow on the way ）, The back ones are all pressed 360 degree （ namely 2π） For the cycle . That is, the angle is actually according to 2.5π,4.5π,6.5π…… The law comes , The corresponding angle formula is actually ：

So the adjusted sine curve code is ：

class SineCurve extends Curve {
 final int count;
 const SineCurve({this.count = 1}) : assert(count > 0);

 @override
 double transformInternal(double t) {
 //  Need compensation pi/2 Angles , So that the starting value is 0. The end value is 1, Avoid the last sudden return to 0
 return sin(2 * (count + 0.25) * pi * t);
 }
}


Let's look at the effect after adjustment , Is it a smooth transition ？

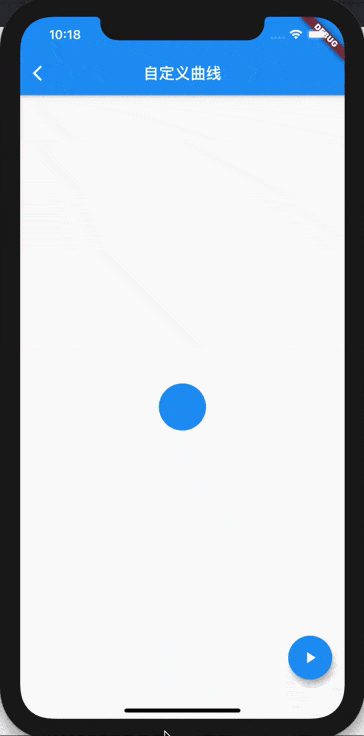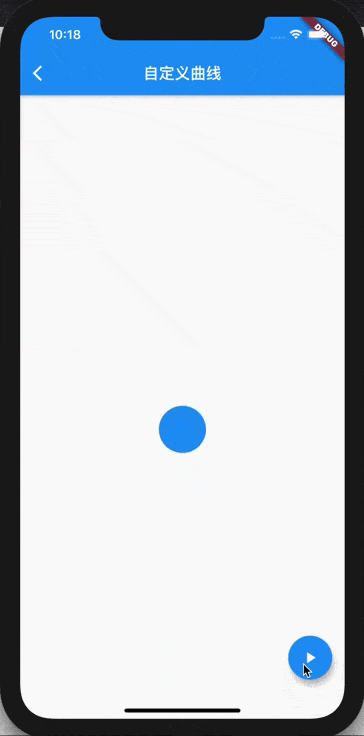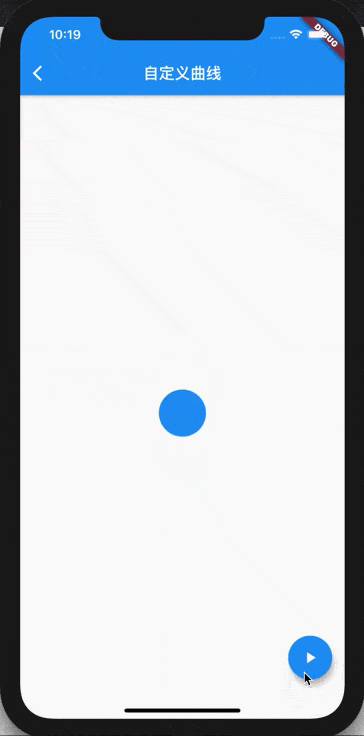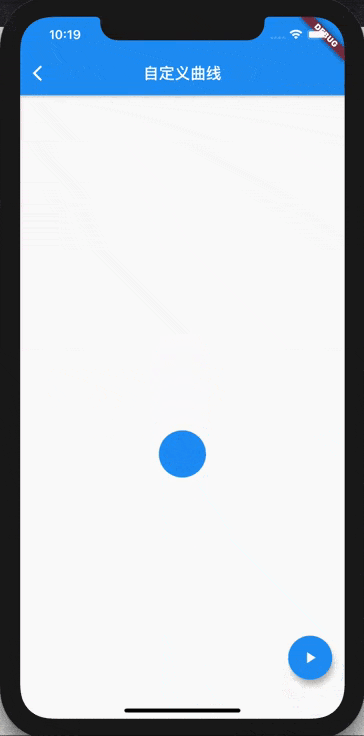
summary

This article introduces  Flutter  The principle of animation curve class and the mechanism of controlling animation , actually  Curve  Class is in a specified time , Complete the transition from start to end along the curve . But in order to ensure smooth animation transition , You should ensure the of custom curves

transformInternal

The starting value and ending value of the return value of the method are 0 and 1.

Welcome to follow individual public number ：

Ma Nong on the island

, Or add this wechat ：

island-coder

.