Sword finger offer 51. reverse pairs in the array

Catalog

subject

Ideas

Answer key

Complexity analysis

---

subject

Two numbers in an array , If the number in front is greater than the number in the back , Then these two numbers form a reverse order pair . Enter an array , Find the total number of reverse pairs in this array . 

Time complexity ： Merge sort O(nlog⁡n)O(n \log n)O(nlogn).
Spatial complexity ： Merge sort O(n)O(n)O(n), Because merge sort requires a temporary array .

author ：LeetCode-Solution
link ：https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solution/shu-zu-zhong-de-ni-xu-dui-by-leetcode-solution/
source ： Power button （LeetCode）
The copyright belongs to the author . Commercial reprint please contact the author for authorization , Non-commercial reprint please indicate the source .

Limit ：0 <= The length of the array <= 50000

Ideas

The reverse ： The elements in front of the array > The elements behind

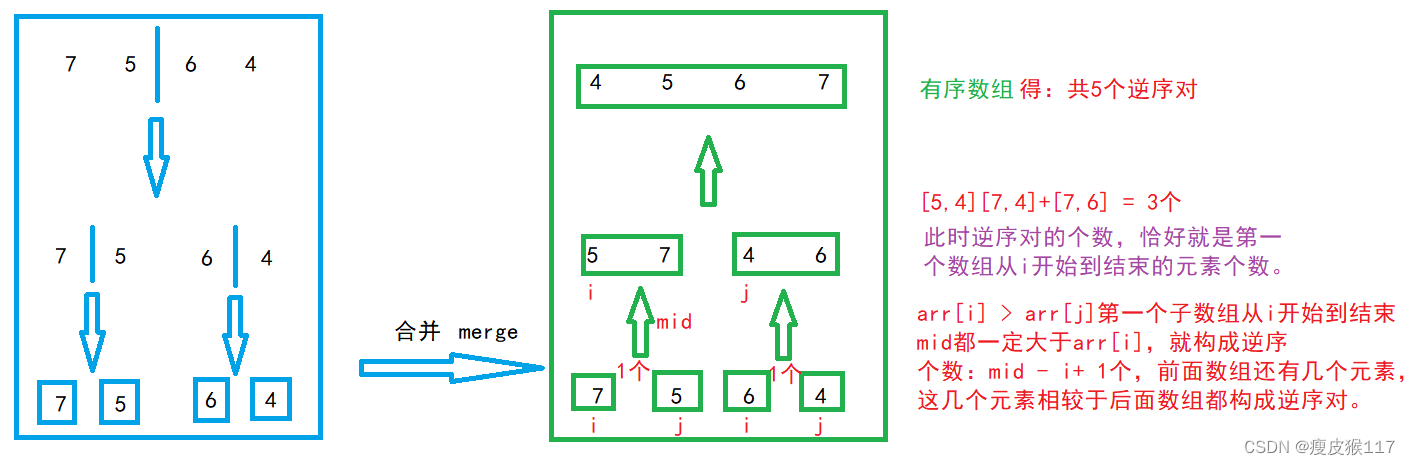
The idea of merging and sorting can be used , Find the reverse order pair in the merging process .
merge It happens to be the previous array element > The following subarray elements are merged , Conform to the definition in reverse order .

Is in the merge sort merge In the process of , Incidentally, I find the number of pairs in reverse order .

Only if both subarrays still have elements and the elements of the first subarray arr[i] > arr[j] It is possible to form a reverse order pair , And the number of reverse pairs is exactly the number of the first array from i Number of remaining elements from start to end .

merge Set in operation count Counter , Count the number of pairs in reverse order .

Answer key

/**
 *  The finger of the sword  Offer 51.  Reverse pairs in arrays 
 */
public class Offer51_reversePairs {
    public int reversePairs(int[] nums) {
        return reversePairsInternal(nums, 0, nums.length - 1);
    }

    /**
     *  stay nums[l..r] Merge and sort on , Returns the number of sorted pairs in reverse order 
     */
    private int reversePairsInternal(int[] nums, int l, int r) {
        //  The array is empty or has only one element 
        if (l >= r) {
            return 0;
        }
        int mid = l + (r - l) / 2;
        //  First, find the number of pairs in reverse order of the first sub array 
        int leftCount = reversePairsInternal(nums, l, mid);
        //  Then find the number of pairs in reverse order of the second sub array 
        int rightCount = reversePairsInternal(nums, mid + 1, r);
        if (nums[mid] > nums[mid + 1]) {
            //  After the left and right arrays are ordered , There is also a reverse order between the two arrays ,merge Process to find the number of pairs in reverse order in the consolidation process 
            return leftCount + rightCount + merge(nums, l, mid, r);
        }
        // nums[mid] < nums[mid + 1] The whole array has been ordered , There can be no reverse order ！
        return leftCount + rightCount;
    }

    /**
     *  Merge two ordered subarrays nums[l..mid] nums[mid + 1..r] Returns the number of pairs in reverse order after merging 
     */
    private int merge(int[] nums, int l, int mid, int r) {
        //  The number of reverse order pairs generated during merging 
        int count = 0;
        int aux[] = new int[r - l + 1];
        for (int i = l; i <= r; i++) {
            aux[i - l] = nums[i];
        }
        int i = l, j = mid + 1;
        for (int k = l; k <= r; k++) {
            if (i > mid) {
                //  The first array has been processed , Directly splice the second array , At this time, there is no reverse order 
                nums[k] = aux[j - l];
                j++;
            } else if (j > r) {
                //  The second array has been processed , Directly splice the first array , At this time, there is no reverse order 
                nums[k] = aux[i - l];
                i++;
            } else if (aux[i - l] <= aux[j - l]) {
                //  Splice the first array , There is no reverse order at this time 
                nums[k] = aux[i - l];
                i++;
            } else {
                //  At this point, the first array element  >  The second array element ,
                //  from i Start to mid All elements that end are compared to arr[j] It's all in reverse order 
                //  The number of pairs in reverse order is exactly mid - i + 1
                count += mid - i + 1;
                nums[k] = aux[j - l];
                j++;
            }
        }
        return count;
    }
}

Complexity analysis

Time complexity ： Merge sort O(nlog⁡n).
Spatial complexity ： Merge sort O(n), Because merge sort requires a temporary array .