当前位置:网站首页>Machine learning support vector machine SVM
Machine learning support vector machine SVM
2022-07-03 20:01:00 【Tc. Xiaohao】
List of articles
SVM Is a very elegant Algorithm , Have perfect mathematical theory , Although not much is used in industry nowadays , But I decided to spend some time writing an article to sort it out .
One support vector
1.0 brief introduction
Support vector machine (support vector machines, SVM) It's a two category model , Its basic model is the linear classifier with the largest interval defined in the feature space , The maximum spacing makes it different from the perceptron ;SVM And nuclear techniques , This makes it a non-linear classifier in essence .SVM The learning strategy is to maximize the interval , It can be formalized as a problem of solving convex quadratic programming , It is also equivalent to the minimization of the regularized hinge loss function .SVM The learning algorithm of is the optimization algorithm for solving convex quadratic programming .
1.1 Algorithmic thought
Here is a list to understand :
A brave man met the demon king in order to save the princess boss, The demon king set a test for him. If the brave can pass the test, return the princess to him , There are some red balls and basketball on the table , Ask the brave to separate them with a stick , requirement : Try to put more balls after , Still apply .
This problem can be solved by constantly adjusting the position of the stick and keeping the maximum distance between the ball on both sides as far as possible .
Then the demon king upgraded the challenge , He placed the two balls in a disorderly way, making it impossible to use a straight stick to separate the two balls 
This is certainly not difficult for our brave , The brave man slapped the table hard and hit the balls in the air. Then he quickly grabbed a piece of paper in the air and stuffed it in to separate the balls of two colors 
The demon king was surprised , I still have this kind of operation , I took it , Only the princess can be returned to the brave
Finally, boring people call these balls ( data )data, Call the stick ( classifier )classifier, Find the biggest gap trick be called ( Optimize )optimization, Beating the table is called ( Nuclear transformation )kernelling, The paper is called ( hyperplane )hyperplane.
Through the above examples, we can understand svm The role of the , If the data is linearly separable , We can separate them with only one straight line , At this time, you only need to maximize the distance between the ball on the side and the straight line , This is the optimization process .
When we encounter the problem of linear indivisibility , Just use a kind of table beating trick, That is, corresponding to our kernel transformation (kernel), Then use hyperplane to classify the data in high-dimensional space .
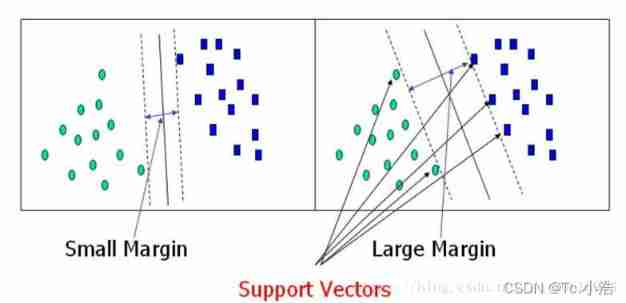
Decision boundaries : It's the line in the middle of the figure , Used to judge classification
Support vector : It refers to the data closest to the decision boundary on the left and right sides of the graph
The largest interval : Select the support vector farthest from the decision boundary , That is, the optimal solution we are looking for
First, consider two-dimensional space , The decision equation is defined as y=wx+b Corresponding R n R^n Rn
A hyperplane in S among w Is the normal vector of the hyperplane ,b intercept 
According to the calculation method of point to surface distance, we can get d i s t a n c e = 1 ∣ ∣ w ∣ ∣ ∣ w x i + b ∣ distance=\frac{1}{||w||}|wx_i+b| distance=∣∣w∣∣1∣wxi+b∣

Before derivation , Let's start with some definitions . Suppose a training data set on the feature space is given

among ![[ The formula ]](/img/d3/8a388dfaf660b6a4e227129b55453f.png) ,
,
x i x_i xi, For the first time i eigenvectors , y i y_i yi Tag for class , When it's equal to +1 Time is positive ; by -1 Time is negative . Suppose that the training data set is linearly separable .
Geometric interval : For a given data set T And hyperplane w ∗ x + b w*x+b w∗x+b , Define the hyperplane about the sample point ( x i , y i ) (x_i,y_i) (xi,yi) The geometric interval of is 
Because we want the maximum interval , So the optimization goal is
Find a line (w and b), Make the point closest to the line farthest
a r g m a x w , b [ 1 / ∣ ∣ w ∣ ∣ m i n i ( y i ( w x i + b ) ) ] argmax_{ w,b} [ 1/∣∣w∣∣min_i (y_i (wx_i +b))] argmaxw,b[1/∣∣w∣∣mini(yi(wxi+b))]
argmax Is the maximum distance min Is to find the nearest support vector , because y i ( w x i + b ) = 1 y_i(wx_i+b)=1 yi(wxi+b)=1 So all that's left is
The current goal :
m a x w , b 1 / ∣ ∣ w ∣ ∣ max _{w,b }1/∣∣w∣| maxw,b1/∣∣w∣∣
Because our learning algorithm generally likes to find the minimum loss, we turn the problem into
Routine routine : The problem of solving the maximum value is transformed into the problem of solving the minimum value 
For the convenience of derivation, we multiply 1 2 \frac{1}{2} 21 Square is also for derivation because ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ yes 2 Norms are signed with roots for the convenience of derivation
solve : Apply Lagrange
The problem has been transformed into a convex quadratic programming problem, so it can be solved by Lagrange dual method , The premise is that our objective function must be convex , Because only convex functions can guarantee the existence of global optimal solutions , This is associated with convex optimization , Our hyperplane is a convex . The problem of finding the optimal solution usually exists in the following types
1) Unrestricted : The objective function without constraints is ) m i n f ( x ) minf(x) minf(x) Directly use Fermat lemma to find the extreme value of the derivative solution of the objective function
2) Equality constraints : There is an equation h j ( x ) , j = 1 , 2 , . . . m h_j(x),j=1,2,...m hj(x),j=1,2,...m Under the circumstances , It is necessary to use Lagrange multiplier method to introduce multiplier vector and f(x) m i n f ( x ) minf(x) minf(x) Construct a new objective function to solve .
3) Unequal constraints : There are unequal constraints g i ( x ) < = 0 , i = 1 , 2... n g_i(x)<=0,i=1,2...n gi(x)<=0,i=1,2...n There may also be equality constraints h j ( x ) , j = 1 , 2 , . . . m h_j(x),j=1,2,...m hj(x),j=1,2,...m At this time, we also need to construct a new objective function with these constraints and multiplier vectors , adopt KKT The necessary condition that the condition can solve the optimal value .
【kkt Conditions 】
After being processed by Lagrange function x The derivative is 0
h i ( x ) = 0 h_i(x)=0 hi(x)=0
g j ( x ) < = 0 g_j(x)<=0 gj(x)<=0

Soft space
The above conditions assume that the data are completely linearly separable , When the data is not completely linearly separable and there is noise, we need to introduce a relaxation factor 
Experimental part
from sklearn.svm import SVC
from sklearn import datasets
iris=datasets.load_iris()
# Select all samples , Take the second and third feature
X=iris['data'][:,(2,3)]
y=iris['target']
# Take two categories
setosa_or=(y==0)|(y==1)
X=X[setosa_or]
y=y[setosa_or]
svm_clf=SVC(kernel='linear',C=float('inf'))
svm_clf.fit(X,y)
# Data from 0 To 5.5 Yes 200 individual
x0=np.linspace(0,5.5,200)
# Three curves
pred_1=5*x0-20
pred_2=x0-1.8
pred_3=0.1*x0+0.5
def plot_svc_decision_boundary(svm_clf,xmin,xmax,sv=True):
# The weight
w=svm_clf.coef_[0]
# bias
b=svm_clf.intercept_[0]
decison_boundary=-w[0]/w[1]*x0-b/w[1]
margin=1/w[1]
# Upper boundary
gutter_up=decison_boundary+margin
# Lower boundary
gutter_down=decison_boundary-margin
if sv:
svs=svm_clf.support_vectors_
plt.scatter(svs[:,0],svs[:,1],s=180,facecolors='#FFAAAA')
plt.plot(x0,decison_boundary,'k-',linewidth=2)
plt.plot(x0,gutter_up,'k--',linewidth=2)
plt.plot(x0,gutter_down,'k--',linewidth=2)
plt.figure(figsize=(14,4))
plt.subplot(121)
# Yellow and blue data points
plt.plot(X[:,0][y==1],X[:,1][y==1],'bs')
plt.plot(X[:,0][y==0],X[:,1][y==0],'ys')
# Three lines
plt.plot(x0,pred_1,'g--',linewidth=2)
plt.plot(x0,pred_2,'m--',linewidth=2)
plt.plot(x0,pred_3,'r--',linewidth=2)
plt.axis([0,5.5,0,2])
plt.subplot(122)
plot_svc_decision_boundary(svm_clf,0,5.5)
plt.plot(X[:,0][y==1],X[:,1][y==1],'bs')
plt.plot(X[:,0][y==0],X[:,1][y==0],'ys')
plt.axis([0,5.5,0,2])
The effect is as follows 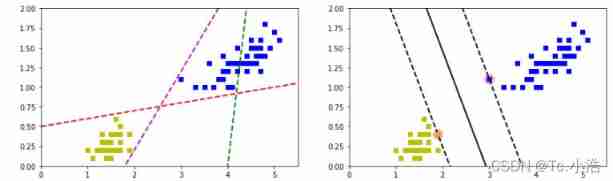
边栏推荐
- Chapter 1: recursively find the factorial n of n!
- How to read the source code [debug and observe the source code]
- Popularize the basics of IP routing
- 2022-07-02 网工进阶(十五)路由策略-Route-Policy特性、策略路由(Policy-Based Routing)、MQC(模块化QoS命令行)
- 2022 - 06 - 30 networker Advanced (XIV) Routing Policy Matching Tool [ACL, IP prefix list] and policy tool [Filter Policy]
- Change deepin to Alibaba image source
- Realize user registration and login
- Global and Chinese market of micro positioning technology 2022-2028: Research Report on technology, participants, trends, market size and share
- Rd file name conflict when extending a S4 method of some other package
- NFT without IPFs and completely on the chain?
猜你喜欢
Phpstudy set LAN access

2022-06-25 网工进阶(十一)IS-IS-三大表(邻居表、路由表、链路状态数据库表)、LSP、CSNP、PSNP、LSP的同步过程
IPv6 experiment

Network security Kali penetration learning how to get started with web penetration how to scan based on nmap
![Chapter 2: find the number of daffodils based on decomposition, find the number of daffodils based on combination, find the conformal number in [x, y], explore the n-bit conformal number, recursively](/img/c5/0081689817700770f6210d50ec4e1f.png)
Chapter 2: find the number of daffodils based on decomposition, find the number of daffodils based on combination, find the conformal number in [x, y], explore the n-bit conformal number, recursively

2022-06-30 网工进阶(十四)路由策略-匹配工具【ACL、IP-Prefix List】、策略工具【Filter-Policy】
BOC protected alanine zinc porphyrin Zn · TAPP ala BOC / alanine zinc porphyrin Zn · TAPP ala BOC / alanine zinc porphyrin Zn · TAPP ala BOC / alanine zinc porphyrin Zn · TAPP ala BOC supplied by Qiyu
2022-06-27 网工进阶(十二)IS-IS-开销类型、开销计算、LSP的处理机制、路由撤销、路由渗透
Chapter 2: find the box array, complete number in the specified interval, and improve the complete number in the specified interval

Chapter 1: seek common? Decimal and S (D, n)
随机推荐
03 -- QT OpenGL EBO draw triangle
Find a line in a file and remove it
Use unique_ PTR forward declaration? [repetition] - forward declaration with unique_ ptr? [duplicate]
Global and Chinese market of cyanuric acid 2022-2028: Research Report on technology, participants, trends, market size and share
Explore the internal mechanism of modern browsers (I) (original translation)
4. Data splitting of Flink real-time project
Vscode reports an error according to the go plug-in go get connectex: a connection attempt failed because the connected party did not pro
PR 2021 quick start tutorial, how to create new projects and basic settings of preferences?
AcWing 1460. Where am i?
05 -- QT OpenGL draw cube uniform
Global and Chinese markets of cast iron diaphragm valves 2022-2028: Research Report on technology, participants, trends, market size and share
Titles can only be retrieved in PHP via curl - header only retrieval in PHP via curl
Microservice knowledge sorting - search technology and automatic deployment technology
Chapter 1: find the factorial n of n!
1.5 learn to find mistakes first
Professional interpretation | how to become an SQL developer
FAQs for datawhale learning!
Chapter 2: find the box array, complete number in the specified interval, and improve the complete number in the specified interval
Exercises of function recursion
[effective Objective-C] - block and grand central distribution