Stack Title: exclusive time of function

subject

Title and provenance

title ： Exclusive time of function

Source ：636. Exclusive time of function

difficulty

6 level

Title Description

requirement

There is one Single thread CPU Running a program containing $\text{n}$ Program of trace function . Each function has a function located in $\text{0}$ and $\text{n - 1}$ Unique identifier between .

Function call Stored on a call stack ： When a function call starts , Its identifier will be pushed onto the stack . And when a function call ends , Its identifier will pop up from the stack . The function with the identifier at the top of the stack is The currently executing function . Whenever a function starts or ends , A log will be recorded , Include function identifiers 、 Is it the beginning or the end 、 And the corresponding timestamp .

Give you a list of logs $\text{logs}$, among $\text{logs[i]}$ It means the first one $\text{i}$ Log messages , The message is a press $\text{"{function\_id}:{"start" | "end"}:{timestamp}"}$ Formatted string . for example ,$\text{"0:start:3"}$ Means the identifier is $\text{0}$ Function call in timestamp $\text{3}$ Of Start execution ; and $\text{"1:end:2"}$ Means the identifier is $\text{1}$ Function call in timestamp $\text{2}$ Of End execution . Be careful , A function can Call several times , There may be recursive calls .

Functional Exclusive time The definition is the sum of the execution time of this function in all function calls of the program , The time spent calling other functions does not count as the exclusive time of the function . for example , If a function is called twice , One call to execute $\text{2}$ Unit time , Another call to execute $\text{1}$ Unit time , Then the Exclusive time by $\text{2 + 1 = 3}$.

Returns the of each function as an array Exclusive time , Among them the first $\text{i}$ The value corresponding to each subscript represents the identifier $\text{i}$ Exclusive time of function .

Example

Example 1：

Input ：$\text{n = 2, logs = ["0:start:0","1:start:2","1:end:5","0:end:6"]}$
Output ：$\text{[3,4]}$
explain ：
function $\text{0}$ At the time stamp $\text{0}$ Start execution at the beginning of , perform $\text{2}$ Unit time , Apply to timestamp $\text{1}$ End of execution .
function $\text{1}$ At the time stamp $\text{2}$ Start execution at the beginning of , perform $\text{4}$ Unit time , Apply to timestamp $\text{5}$ End of execution .
function $\text{0}$ At the time stamp $\text{6}$ Resume execution at the beginning of , perform $\text{1}$ Unit time .
So the function $\text{0}$ Total execution $\text{2 + 1 = 3}$ Unit time , function $\text{1}$ Total execution $\text{4}$ Unit time .

Example 2：

Input ：$\text{n = 1, logs = ["0:start:0","0:start:2","0:end:5","0:start:6","0:end:6","0:end:7"]}$
Output ：$\text{[8]}$
explain ：
function $\text{0}$ At the time stamp $\text{0}$ Start execution at the beginning of , perform $\text{2}$ Unit time , And recursively call itself .
function $\text{0}$（ Recursively call ） At the time stamp $\text{2}$ Start execution at the beginning of , perform $\text{4}$ Unit time .
function $\text{0}$（ Initial call ） Resume execution , And immediately call itself again .
function $\text{0}$（ The second recursive call ） At the time stamp $\text{6}$ Start execution at the beginning of , perform $\text{1}$ Unit time .
function $\text{0}$（ Initial call ） At the time stamp $\text{7}$ The initial recovery execution of , perform $\text{1}$ Unit time .
So the function $\text{0}$ Total execution $\text{2 + 4 + 1 + 1 = 8}$ Unit time .

Example 3：

Input ：$\text{n = 2, logs = ["0:start:0","0:start:2","0:end:5","1:start:6","1:end:6","0:end:7"]}$
Output ：$\text{[7,1]}$
explain ：
function $\text{0}$ At the time stamp $\text{0}$ Start execution at the beginning of , perform $\text{2}$ Unit time , And recursively call itself .
function $\text{0}$（ Recursively call ） At the time stamp $\text{2}$ Start execution at the beginning of , perform 4 Unit time .
function $\text{0}$（ Initial call ） Resume execution , And immediately call the function $\text{1}$.
function $\text{1}$ At the time stamp $\text{6}$ Start execution at the beginning of , perform $\text{1}$ Unit time , Apply to timestamp $\text{6}$ End of execution .
function $\text{0}$（ Initial call ） At the time stamp $\text{7}$ The initial recovery execution of , perform $\text{1}$ Unit time , Apply to timestamp $\text{7}$ End of execution .
So the function $\text{0}$ Total execution $\text{2 + 4 + 1 = 7}$ Unit time , function $\text{1}$ Total execution $\text{1}$ Unit time .

Example 4：

Input ：$\text{n = 2, logs = ["0:start:0","0:start:2","0:end:5","1:start:7","1:end:7","0:end:8"]}$
Output ：$\text{[8,1]}$

Example 5：

Input ：$\text{n = 1, logs = ["0:start:0","0:end:0"]}$
Output ：$\text{[1]}$

Data range

• $\text{1}\le \text{n}\le \text{100}$
• $\text{1}\le \text{logs.length}\le \text{500}$
• $\text{0}\le \text{function\_id}<\text{n}$
• $\text{0}\le \text{timestamp}\le {\text{10}}^{\text{9}}$
• Two start events do not occur at the same time stamp
• Two end events do not occur at the same timestamp
• Each function has a corresponding $\text{"start"}$ The log $\text{"end"}$ journal

solution

Ideas and algorithms

Because the method of function call is stored on the call stack , Therefore, the stack can be used to simulate the function call , The top element of the stack represents the identifier of the function being executed .

For a given log list , The storage order is in the order of timestamp , So you can traverse the log list , Calculate the exclusive time of each function . Each log contains three items of information , Namely ： Function identifier 、 Start or end 、 Time stamp . When calculating function exclusive time , You need to consider the current timestamp and the previous timestamp , And the following different situations need to be considered ：

• The function starts executing , And the stack is empty , No other functions are executing at this time , So there is no need to update the exclusive time of any function , Stack the current function identifier ;

• The function starts executing , And the stack is not empty , At this time, the original function corresponding to the stack top identifier is executing , The time after the new function starts to execute is not included in the exclusive time of the original function , Therefore, you need to update the exclusive time of the original function , Add the difference between the current timestamp and the previous timestamp to the exclusive time of the original function , Then put the current function identifier on the stack ;

• The function ends execution , Because the current timestamp represents the end of the timestamp , Therefore, you need to add the timestamp $1$, At this point, the identifier at the top of the stack must be the same as the current function identifier , The latest exclusive time of the current function is the current timestamp （ Has added $1$） Difference from the previous timestamp , Add the difference between the current timestamp and the previous timestamp to the exclusive time of the current function , And push the top element out of the stack , If the stack is not empty after the top element is out of the stack , Then the new stack top element is the original function to restore the exclusive time .

After processing a log , Save the current timestamp as the previous timestamp , Then process the next log , Until all logs are processed , You can get the exclusive time of each function .

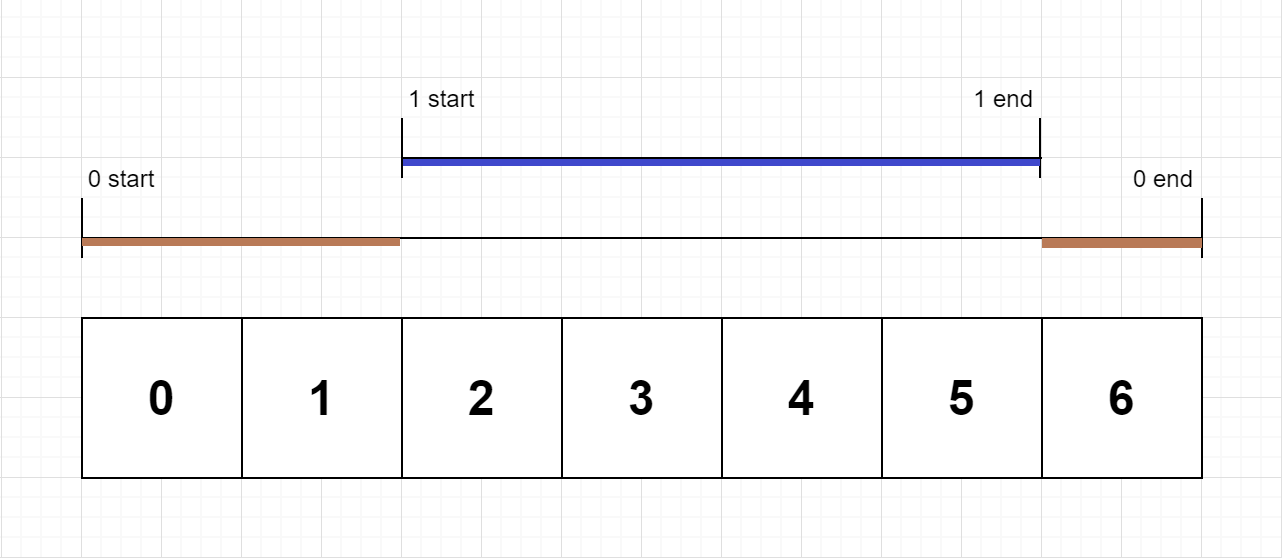
Example 3 The exclusive time of the function of is shown in the figure below .

The exclusive time of the function is calculated as follows . At the beginning $\text{time}=[0,0]$.

$[\text{0:start:0}]$： Function identifier $\text{id}=0$, Time stamp $\text{timestamp}=0$, take $0$ Push ,$\text{time}=[0,0]$;

$[\text{0:start:2}]$： Function identifier $\text{id}=0$, Time stamp $\text{timestamp}=2$, take $2-0=2$ Add to $\text{time}[0]$, take $0$ Push ,$\text{time}=[2,0]$;

$[\text{0:end:5}]$： Function identifier $\text{id}=0$, Time stamp $\text{timestamp}=5+1=6$, take $6-2=4$ Add to $\text{time}[0]$, take $0$ Out of the stack ,$\text{time}=[6,0]$;

$[\text{1:start:6}]$： Function identifier $\text{id}=1$, Time stamp $\text{timestamp}=6$, take $6-6=0$ Add to $\text{time}[0]$, take $1$ Push ,$\text{time}=[6,0]$;

$[\text{1:end:6}]$： Function identifier $\text{id}=1$, Time stamp $\text{timestamp}=6+1=7$, take $7-6=1$ Add to $\text{time}[1]$, take $1$ Out of the stack ,$\text{time}=[6,1]$;

$[\text{0:end:7}]$： Function identifier $\text{id}=0$, Time stamp $\text{timestamp}=7+1=8$, take $8-7=1$ Add to $\text{time}[0]$, take $0$ Out of the stack ,$\text{time}=[7,1]$.

Code

class Solution {
    
    public int[] exclusiveTime(int n, List<String> logs) {
    
        int[] time = new int[n];
        Deque<Integer> stack = new ArrayDeque<Integer>();
        int prevTimestamp = 0;
        int size = logs.size();
        for (int i = 0; i < size; i++) {
    
            String log = logs.get(i);
            String[] logArray = log.split(":");
            int id = Integer.parseInt(logArray[0]);
            String action = logArray[1];
            int timestamp = Integer.parseInt(logArray[2]);
            if ("start".equals(action)) {
    
                if (!stack.isEmpty()) {
    
                    int prevId = stack.peek();
                    time[prevId] += timestamp - prevTimestamp;
                }
                stack.push(id);
            } else if ("end".equals(action)) {
    
                timestamp++;
                time[id] += timestamp - prevTimestamp;
                stack.pop();
            }
            prevTimestamp = timestamp;
        }
        return time;
    }
}

Complexity analysis

• Time complexity ：$O(m)$, among $m$ Is a list of logs $\text{logs}$ The length of . You need to traverse the log list once , The operation time for each log is $O(1)$.

• Spatial complexity ：$O(m)$, among $m$ Is a list of logs $\text{logs}$ The length of . The space complexity mainly depends on the stack space , The stack stores the called function , The number of elements in the stack does not exceed $\frac{m}{2}$. The return value is not included in the space complexity .