当前位置:网站首页>二叉树的四种遍历方式以及中序后序、前序中序、前序后序、层序创建二叉树【专为力扣刷题而打造】
二叉树的四种遍历方式以及中序后序、前序中序、前序后序、层序创建二叉树【专为力扣刷题而打造】
2022-07-04 19:05:00 【@了凡】
博主介绍:
– 我是了 凡 微信公众号【了凡银河系】期待你的关注。未来大家一起加油啊~
前言
这里三种遍历方式不用过多介绍,相信学过数据结构的人都可以轻松使用递归方式进行遍历,非递归方式思想也是一致的。
根据前序中序、中序后序、前序后序均参考力扣题解所写,只有层序遍历是为了再力扣解题不方便所以才选择在本地解题,但是本地解题不能进行测试,使用其他三种创建方式又过于麻烦,所以想使用层序创建二叉树,思维比较简单供大家参考,有问题可以及时讨论。
前序遍历
由于是前序遍历所以根节点一定在前,遍历顺序为(根、左、右)
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// 前序遍历
func preorderTraversal(root *TreeNode) []int {
nums := make([]int, 0)
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node != nil {
nums = append(nums, node.Val) // 根
dfs(node.Left) // 左
dfs(node.Right) // 右
}
}
dfs(root)
return nums
}
中序遍历
由于是中序遍历所以根节点一定在中间,遍历顺序为(左、根、右)
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// 中序遍历
func inorderTraversal(root *TreeNode) []int {
nums := make([]int, 0)
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node != nil {
dfs(node.Left) // 左
nums = append(nums, node.Val) // 根
dfs(node.Right) // 右
}
}
dfs(root)
return nums
}
后序遍历
由于是后序遍历所以根节点一定在后面,遍历顺序为(左、右、根)
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// 后续遍历
func postorderTraversal(root *TreeNode) []int {
nums := make([]int, 0)
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node != nil {
dfs(node.Left)
dfs(node.Right)
nums = append(nums, node.Val)
}
}
dfs(root)
return nums
}
层序遍历
层序遍历肯定是一行一行的遍历,其思想就是BFS(像一滴水滴进水潭里的波纹一样一层一层的),这里使用队列不断的暂存下一个子孩子当作下一次的根节点进行遍历它的子孩子。
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// 层序遍历
func levelOrder(root *TreeNode) [][]int {
ret := [][]int{
}
if root == nil {
return ret
}
q := []*TreeNode{
root}
for i := 0; len(q) > 0; i++ {
ret = append(ret, []int{
})
p := []*TreeNode{
}
for j := 0; j < len(q); j++ {
node := q[j]
ret[i] = append(ret[i], node.Val)
if node.Left != nil {
p = append(p, node.Left)
}
if node.Right != nil {
p = append(p, node.Right)
}
}
q = p
}
return ret
}
层序创建二叉树
到了重点时刻了,以参考层序遍历为相反思维,首先对一维数组进行拆分成每一层节点,做出二维数组,之后根据遍历每一个孩子当作当前的根节点添加的它的左右孩子。此写法较为丑陋且性能较低,望耐心扣底。这里-1代表空值
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// 层序创建二叉树
func sequenceCreation(nums []int) *TreeNode {
if len(nums) == 0 {
return nil
}
if len(nums) == 1 {
return &TreeNode{
nums[0], nil, nil}
}
// 先对数组进行分层分割
sliNums := make([][]int, 0)
count := 1
for i := 0; i < len(nums); {
cont := make([]int, 0)
j := i
for ; j < i+count; j++ {
cont = append(cont, nums[j])
}
i = j
sliNums = append(sliNums, cont)
count *= 2
}
root := new(TreeNode)
root.Val = sliNums[0][0]
queue := []*TreeNode{
root}
count = 0
for i := 1; i < len(sliNums); i++ {
for j := 0; j < len(sliNums[i]); j += 2 {
if sliNums[i][j] != -1 {
queue[count].Left = &TreeNode{
Val: sliNums[i][j]}
queue = append(queue, queue[count].Left)
} else {
if queue[count] != nil {
queue[count].Left = nil
queue = append(queue, queue[count].Left)
}
}
if sliNums[i][j+1] != -1 {
queue[count].Right = &TreeNode{
Val: sliNums[i][j+1]}
queue = append(queue, queue[count].Right)
} else {
if queue[count] != nil {
queue[count].Right = nil
queue = append(queue, queue[count].Right)
}
}
count++
}
}
return root
}
使用案例
这里以力扣的简单题为例:104. 二叉树的最大深度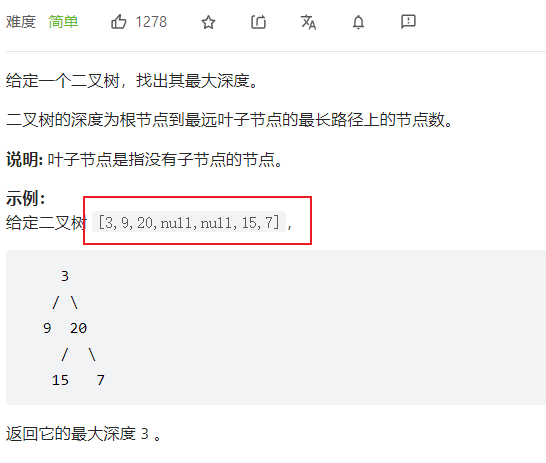
代码实现
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func maxDepth(root *TreeNode) int {
if root == nil {
return 0
}
return max(maxDepth(root.Left), maxDepth(root.Right)) + 1
}
func main() {
nums := []int{
3, 9, 20, -1, -1, 15, 7}
root := sequenceCreation(nums) // 这个函数就是上述的层序遍历,在这里就不重复粘贴了
fmt.Println(maxDepth(root))
}
测试结果
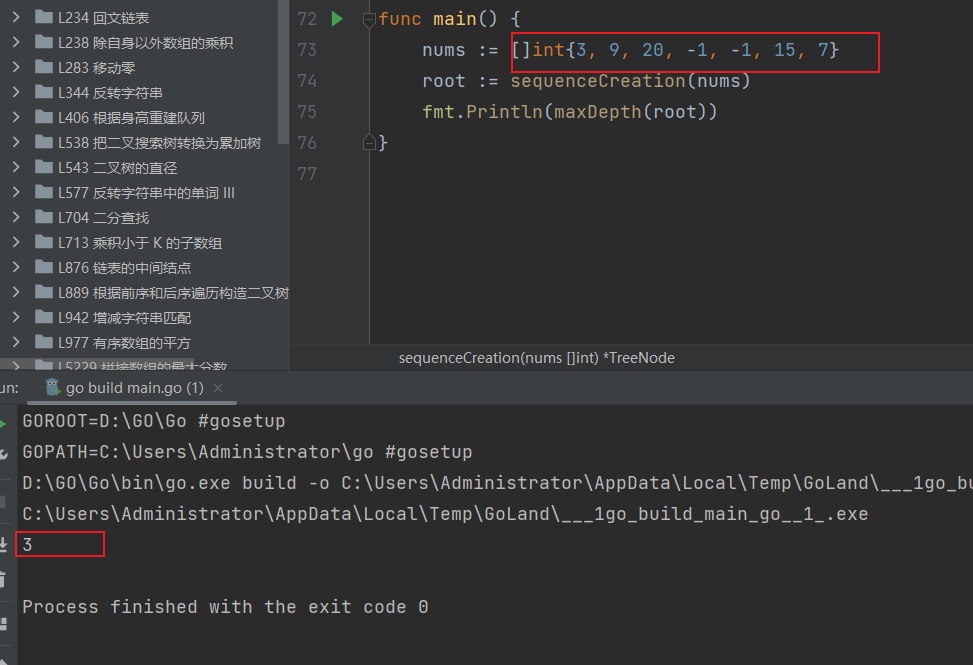
结果正确
前序中序创建二叉树
这里参考力扣题解,思维比较简单,preorder切片的开始都是根节点,然后和inorder切片进行比较就可以找到左右孩子,不断向下重复比对就可以进行创建完成。
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// 前序找根节点,中序找左右分界线
func pIBuildTree(preorder []int, inorder []int) *TreeNode {
if len(preorder) == 0 {
return nil
}
root := &TreeNode{
preorder[0], nil, nil}
i := 0
for ; i < len(inorder); i++ {
if inorder[i] == preorder[0] {
break
}
}
root.Left = pIBuildTree(preorder[1:len(inorder[:i])+1], inorder[:i])
root.Right = pIBuildTree(preorder[len(inorder[:i])+1:], inorder[i+1:])
return root
}
中序后序创建二叉树
和前序中序基本一致,只是这次是中序和后序比对
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// 从中序后续创建二叉树
func iPBuildTree(inorder []int, postorder []int) *TreeNode {
idxMap := map[int]int{
}
for i, v := range inorder {
idxMap[v] = i
}
var build func(int, int) *TreeNode
build = func(inorderLeft, inorderRight int) *TreeNode {
// 无剩余节点
if inorderLeft > inorderRight {
return nil
}
// 后序遍历的末尾元素即为当前子树的根节点
val := postorder[len(postorder)-1]
postorder = postorder[:len(postorder)-1]
root := &TreeNode{
Val: val}
// 根据 val 在中序遍历的位置,将中序遍历划分成左右两颗子树
// 由于我们每次都从后序遍历的末尾取元素,所以要先遍历右子树再遍历左子树
inorderRootIndex := idxMap[val]
root.Right = build(inorderRootIndex+1, inorderRight)
root.Left = build(inorderLeft, inorderRootIndex-1)
return root
}
return build(0, len(inorder)-1)
}
前序后序创建二叉树
这里结果可能不唯一
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// 根据前序后续构建二叉树
func constructFromPrePost(preorder []int, postorder []int) *TreeNode {
// 递归结束条件
if len(preorder) == 0 {
return nil
}
// 只有一个元素时,为叶子节点。这一步在889不可省略
if len(preorder) == 1 {
return &TreeNode{
Val: preorder[0]}
}
// 根节点
root := &TreeNode{
Val: preorder[0]}
// 在后序序列中寻找和前序序列根节点下一个节点相等的位置
for pos, node := range postorder {
if node == preorder[1] {
// 构建左子树
root.Left = constructFromPrePost(preorder[1:pos+2], postorder[:pos+1])
// 构建右子树
root.Right = constructFromPrePost(preorder[pos+2:], postorder[pos+1:len(postorder)-1])
break
}
}
return root
}
参考链接:
- 从中序与后序遍历序列构造二叉树:https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solution/cong-zhong-xu-yu-hou-xu-bian-li-xu-lie-gou-zao-14/
- 根据前序和后序遍历构造二叉树:https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-postorder-traversal/solution/889-gen-ju-qian-xu-he-hou-xu-bian-li-gou-zw0i/
- 从前序与中序遍历序列构造二叉树:https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solution/cong-qian-xu-yu-zhong-xu-bian-li-xu-lie-gou-zao-9/
创作不易,点个赞吧!
如果需要后续再看点个收藏!
如果对我的文章有兴趣给个关注!
如果有问题,可以关注公众号【了凡银河系】点击联系我私聊。
边栏推荐
- ICML 2022 | Meta提出鲁棒的多目标贝叶斯优化方法,有效应对输入噪声
- What is the development of block hash quiz game system? Hash quiz game system development (case mature)
- Crystal optoelectronics: ar-hud products of Chang'an dark blue sl03 are supplied by the company
- What financial products can you buy with a deposit of 100000 yuan?
- 九齐单片机NY8B062D单按键控制4种LED状态
- Actual combat simulation │ JWT login authentication
- 更强的 JsonPath 兼容性及性能测试之2022版(Snack3,Fastjson2,jayway.jsonpath)
- 什么叫内卷?
- 漫谈客户端存储技术之Cookie篇
- Template_ Large integer subtraction_ Regardless of size
猜你喜欢
Flet教程之 08 AppBar工具栏基础入门(教程含源码)

Selected review | machine learning technology for Cataract Classification / classification
Pointnet / pointnet++ point cloud data set processing and training
华为nova 10系列支持应用安全检测功能 筑牢手机安全防火墙
![[Beijing Xunwei] i.mx6ull development board porting Debian file system](/img/46/abceaebd8fec2370beec958849de18.jpg)
[Beijing Xunwei] i.mx6ull development board porting Debian file system
Win11无法将值写入注册表项如何解决?

Ziguang zhanrui completed the first 5g R17 IOT NTN satellite on the Internet of things in the world

What are the consequences of closing the read / write channel?
Flet教程之 04 FilledTonalButton基础入门(教程含源码)
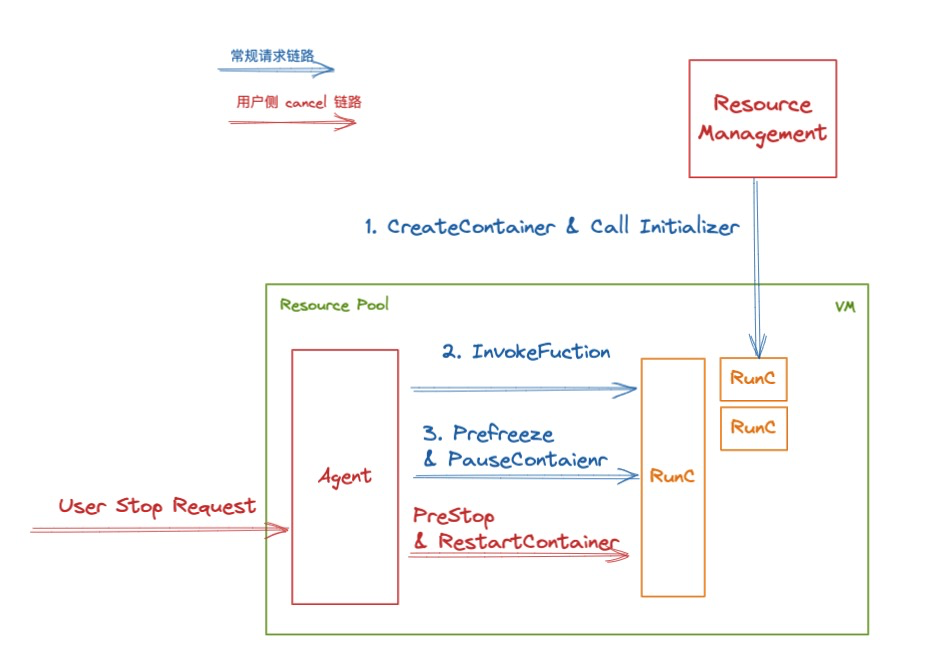
解密函数计算异步任务能力之「任务的状态及生命周期管理」
随机推荐
Is it safe for Great Wall Securities to open an account? Stock account opening process online account opening
Win11U盘拒绝访问怎么办?Win11U盘拒绝访问的有效解决方法
Flet教程之 06 TextButton基础入门(教程含源码)
为什么最大速度是光速
Detailed explanation of Audi EDI invoice message
2022 version of stronger jsonpath compatibility and performance test (snack3, fastjson2, jayway.jsonpath)
实践示例理解js强缓存协商缓存
Six stones programming: about code, there are six triumphs
Lingyun going to sea | 10 jump &huawei cloud: jointly help Africa's inclusive financial services
Employment prospects of neural network Internet of things application technology [welcome to add]
CDGA|数据治理不得不坚持的六个原则
紫光展锐完成全球首个 5G R17 IoT NTN 卫星物联网上星实测
Write it down once Net analysis of thread burst height of an industrial control data acquisition platform
Qt编写物联网管理平台38-多种数据库支持
Process of manually encrypt the mass-producing firmware and programming ESP devices
#夏日挑战赛#带你玩转HarmonyOS多端钢琴演奏
FS4061A升压8.4V充电IC芯片和FS4061B升压12.6V充电IC芯片规格书datasheet
New wizard effect used by BCG
Prometheus installation
What is the application technology of neural network and Internet of things