当前位置:网站首页>【4.9 容斥原理详解】
【4.9 容斥原理详解】
2022-07-26 22:38:00 【浪漫主义狗】
更好的阅读体验 \color{red}{更好的阅读体验} 更好的阅读体验
思想

求 S = S 1 ∪ S 2 ∪ S 3 S=S_1\cup S_2\cup S_3 S=S1∪S2∪S3的面积:
由图可知 : S = S 1 ∪ S 2 ∪ S 3 = S 1 + S 2 + S 3 − S 1 ∩ S 2 − S 1 ∩ S 3 − S 2 ∩ S 3 + S 1 ∩ S 2 ∩ S 3 \begin{aligned} 由图可知:S=&S_1\cup S_2\cup S_3\\ =&S_1+S_2+S_3\\ &-S_1\cap S_2-S_1\cap S_3-S_2\cap S_3\\ &+S_1\cap S_2\cap S_3 \end{aligned} 由图可知:S==S1∪S2∪S3S1+S2+S3−S1∩S2−S1∩S3−S2∩S3+S1∩S2∩S3推广求 S = S 1 ∪ S 2 ∪ S 3 ∩ S 4 S=S_1\cup S_2\cup S_3\cap S_4 S=S1∪S2∪S3∩S4的面积:
S = S 1 ∪ S 2 ∪ S 3 ∩ S 4 = S 1 + S 2 + S 3 + S 4 − S 1 ∩ S 2 − S 1 ∩ S 3 − S 1 ∩ S 4 − S 2 ∩ S 3 − S 2 ∩ S 4 − S 3 ∩ S 4 + S 1 ∩ S 2 ∩ S 3 + S 1 ∩ S 2 ∩ S 4 + S 1 ∩ S 3 ∩ S 4 + S 2 ∩ S 3 ∩ S 4 − S 1 ∩ S 2 ∩ S 3 ∩ S 4 \begin{aligned} S=&S_1\cup S_2\cup S_3\cap S_4\\ =&S_1+S_2+S_3+S_4\\ &-S_1\cap S_2-S_1\cap S_3-S_1\cap S_4-S_2\cap S_3-S_2\cap S_4-S_3\cap S_4\\ &+S_1\cap S_2\cap S_3+S_1\cap S_2\cap S_4+S_1\cap S_3\cap S_4+S_2\cap S_3\cap S_4\\ &-S_1\cap S_2\cap S_3\cap S_4 \end{aligned} S==S1∪S2∪S3∩S4S1+S2+S3+S4−S1∩S2−S1∩S3−S1∩S4−S2∩S3−S2∩S4−S3∩S4+S1∩S2∩S3+S1∩S2∩S4+S1∩S3∩S4+S2∩S3∩S4−S1∩S2∩S3∩S4若将面积作为集合看待,则容易推出:
设 U 中元素有 n 种不同的属性,而第 i 种属性称为 P i 拥有属性 P i 的元素构成集合 S i , 那么 ∣ ⋃ i = 1 n S i ∣ = ∑ i ∣ S i ∣ − ∑ i < j ∣ S i ∩ S j ∣ + ∑ i < j < k ∣ S i ∩ S j ∩ S k ∣ − … + ( − 1 ) m − 1 ∑ a i < a i + 1 ∣ ⋂ i = 1 m S a i ∣ + ⋯ + ( − 1 ) n − 1 ∣ S 1 ∩ ⋯ ∩ S n ∣ 即 : ∣ ⋃ i = 1 n S i ∣ = ∑ m = 1 n ( − 1 ) m − 1 ∑ a i < a i + 1 ∣ ⋂ i = 1 m S a i ∣ \begin{aligned} &设U中元素有n种不同的属性,而第i种属性称为P_i拥有属性P_i的元素构成集合S_i,那么\\\\ &\begin{aligned} \Bigg|\bigcup_{i=1}^{n}S_i\Bigg|=&\sum_i|S_i|-\sum_{i\lt j}|S_i\cap S_j|+\sum_{i\lt j\lt k}|S_i\cap S_j\cap S_k|-\dots\\ &+(-1)^{m-1}\sum_{a_i\lt a_{i+1}}\Bigg|\bigcap_{i=1}^mS_{a_i}\Bigg|+\dots+(-1)^{n-1}|S_1\cap\dots\cap S_n|\\ \end{aligned}\\\\ &即:\\\\ &\Bigg|\bigcup_{i=1}^{n}S_i\Bigg|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i\lt a_{i+1}}\Bigg|\bigcap_{i=1}^mS_{a_i}\Bigg| \end{aligned} 设U中元素有n种不同的属性,而第i种属性称为Pi拥有属性Pi的元素构成集合Si,那么∣∣i=1⋃nSi∣∣=i∑∣Si∣−i<j∑∣Si∩Sj∣+i<j<k∑∣Si∩Sj∩Sk∣−…+(−1)m−1ai<ai+1∑∣∣i=1⋂mSai∣∣+⋯+(−1)n−1∣S1∩⋯∩Sn∣即:∣∣i=1⋃nSi∣∣=m=1∑n(−1)m−1ai<ai+1∑∣∣i=1⋂mSai∣∣
模板例题 890. 能被整除的数
给定一个整数 n 和 m 个不同的质数 p1,p2,…,pm。
请你求出 1∼n 中能被 p1,p2,…,pm 中的至少一个数整除的整数有多少个。
输入格式
第一行包含整数 n 和 m。
第二行包含 m 个质数。
输出格式
输出一个整数,表示满足条件的整数的个数。
数据范围
1≤m≤16,
1≤n,pi≤109
输入样例:
10 2
2 3
输出样例:
7
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=20;
int p[N];
int main(){
int n,m;
cin>>n>>m;
for(int i=0;i<m;i++) cin>>p[i];
LL res=0;
for(int i=1;i<1<<m;i++){
// 1~2^m-1这些数代表2^m-1个不同的项
LL t=1,s=0; //s代表当前枚举的项中包含集合的个数
for(int j=0;j<m;j++){
//看这个项的第 j 位是否包含,1代表包含,0代表不包含
if(i>>j&1){
//选
if(t*p[j]>n){
//此时 n/t = 0,直接break即可
t=-1;
break;
}
t*=p[j];
s++;
}
}
if(t!=-1){
if(s%2) res+=n/t; //加奇数项的个数
else res-=n/t; //减偶数项的个数
}
}
cout<<res<<endl;
return 0;
}
边栏推荐
猜你喜欢

裁剪tif影像

Reduced dimension mean dot product matrix multiplicative norm probability normal distribution square loss

运算符重载

V-viewer use

Find method of web page parsing by crawler

2020-12-20 九九乘法表
Three tier architecture simulation

Comparative simulation of LEACH protocol performance, including the number of dead nodes, data transmission, network energy consumption, the number of cluster heads and load balance
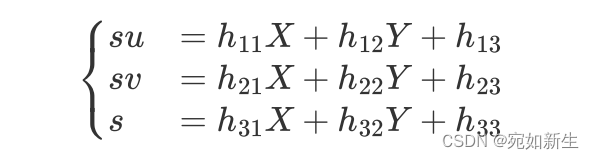
4. Talk about the famous Zhang Zhengyou calibration method

Convolutional neural network -- lenet (pytorch Implementation)
随机推荐
Today's 20220719 toss deeplobcut
Friend友元函数以及单例模式
Torch. correlation function
"Could not load host key" error when xshell connects to the server
JS, one of the methods of object merging Assign (), recursive assignment & method of array merging..., array. Concat (), array. Push. Apply (), array. Push ()
CSDN文章语法规则
C语言 关机小程序
Ubantu installing Oracle JDK
13_集成学习和随机森林(Ensemble Learning and Random Forests)
[LeetCode] 无重复最长字符串
TypeScript(tsconfig.json)
20220720折腾deeplabcut2
9_逻辑回归(Logistic Regression)
生成yolov5.wts文件出错
Downloading and processing of sentinel-2
Lt9611ux Mipi to HDMI 2.0 dual port with audio
运算符重载
今日份20220719折腾deeplabcut
LeetCode——链表篇
C and pointers Chapter 18 runtime environment 18.8 programming exercises