当前位置:网站首页>雇佣收银员(差分约束)
雇佣收银员(差分约束)
2022-07-03 04:37:00 【Snow_raw】
雇佣收银员
Link
题意:
一家超市要每天 24 24 24 小时营业,为了满足营业需求,需要雇佣一大批收银员。已知不同时间段需要的收银员数量不同,为了能够雇佣尽可能少的人员,从而减少成本,这家超市的经理请你来帮忙出谋划策。经理为你提供了一个各个时间段收银员最小需求数量的清单 R ( 0 ) , R ( 1 ) , R ( 2 ) , … , R ( 23 ) 。 R(0),R(1),R(2),…,R(23)。 R(0),R(1),R(2),…,R(23)。 R ( 0 ) R(0) R(0) 表示午夜 00 : 00 00:00 00:00 到凌晨 01 : 00 01:00 01:00 的最小需求数量, R ( 1 ) R(1) R(1) 表示凌晨 01 : 00 01:00 01:00 到凌晨 02 : 00 02:00 02:00 的最小需求数量,以此类推。一共有 N N N 个合格的申请人申请岗位,第 i i i 个申请人可以从 t i ti ti 时刻开始连续工作 8 8 8 小时。收银员之间不存在替换,一定会完整地工作 8 8 8 小时,收银台的数量一定足够。现在给定你收银员的需求清单,请你计算最少需要雇佣多少名收银员。
输入格式:
每组数据输出一个结果,每个结果占一行。如果没有满足需求的安排,输出
No Solution。
数据范围:
0 ≤ R ( 0 ) ≤ 1000 , 0 \le R(0) \le 1000, 0≤R(0)≤1000,
0 ≤ N ≤ 1000 , 0 \le N \le 1000, 0≤N≤1000,
0 ≤ t i ≤ 23 0 \le t_i \le 23 0≤ti≤23
输入样例:
1
1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
5
0
23
22
1
10
思路:
本题存在许多限制关系,即不等式方程,例如:申请人必须连续工作 8 8 8个小时,每个时间段收银员的最小需求数量。且题目所求最少需要雇佣多少名收银员,考虑方向往差分约束方向靠。
题目要求的是最小需求数量,即跑最长路。
找不等式关系方程:由于我们需要约束申请人的 8 8 8个小时,而每个时间段都是图中的一个点,因此本题需要用到前缀和, S [ i ] S[i] S[i]表示 1 1 1~ i i i中所有收银员的数量。
1 : 1: 1: S [ i ] − S [ i − 1 ] > = 0 S[i]-S[i-1]>=0 S[i]−S[i−1]>=0 * \implies * S [ i ] > = S [ i − 1 ] S[i]>=S[i-1] S[i]>=S[i−1]
2 : 2: 2: S [ i ] − S [ i − 1 ] < = p e r s o n [ i ] ( p e r s o n [ i ] 是 i 阶 段 申 请 人 数 量 ) S[i]-S[i-1]<=person[i](person[i]是i阶段申请人数量) S[i]−S[i−1]<=person[i](person[i]是i阶段申请人数量) * \implies * S [ i − 1 ] > = S [ i ] − p e r s o n [ i ] S[i-1]>=S[i]-person[i] S[i−1]>=S[i]−person[i]由于存在环即 23 − 24 23-24 23−24与 1 − 7 1-7 1−7会断开,所以分类讨论。
n u m [ i ] 是 指 当 前 时 间 段 最 少 需 要 的 收 银 员 num[i]是指当前时间段最少需要的收银员 num[i]是指当前时间段最少需要的收银员
3.1 : i < = 7 时 , S [ i ] + S [ 24 ] − S [ 16 + i ] > = n u m [ i ] 3.1:i<=7时,S[i]+S[24]−S[16+i]>=num[i] 3.1:i<=7时,S[i]+S[24]−S[16+i]>=num[i] * \implies * S [ i ] > = S [ 16 + i ] − S [ 24 ] + n u m [ i ] S[i]>=S[16+i]-S[24]+num[i] S[i]>=S[16+i]−S[24]+num[i]
3.2 : i > = 8 时 , S [ i ] − S [ i − 8 ] > = n u m [ i ] 3.2:i>=8 时,S[i]−S[i−8]>=num[i] 3.2:i>=8时,S[i]−S[i−8]>=num[i] * \implies * S [ i ] > = S [ i − 8 ] + R [ i ] S[i]>=S[i-8]+R[i] S[i]>=S[i−8]+R[i]但是我们发现 3.1 3.1 3.1 中出现了两个变量即 S [ 16 + i ] S[16+i] S[16+i]与 S [ 24 ] 。 S[24]。 S[24]。 由于最多出现 1000 1000 1000个人申请收银员,所以我们可以暴力枚举 S [ 24 ] S[24] S[24]的取值从小到大,第一个满足的即是最小的。又因为答案具有单调性,即收银员越多越满足。 所以同样可以使用二分 c h e c k 。 check。 check。
需要注意 c h e c k check check部分中建图同样需要加上两个约束
1 : a d d ( 0 , 24 , x ) 1:add(0,24,x) 1:add(0,24,x)
2 : a d d ( 24 , 0 , − x ) 2:add(24,0,-x) 2:add(24,0,−x)
因为我们已经将 S [ 24 ] S[24] S[24]取常,所以 S [ 24 ] S[24] S[24]的值也应有约束。下面附上暴力枚举和二分 c h e c k check check的代码:
代码1:暴力枚举+差分约束
#include<bits/stdc++.h>
using namespace std;
int t;
int n;
const int N = 30;
const int M = 100;
int e[M],ne[M],idx,w[M];
int h[N];
int num[N];
int person[N];
int dist[N];
bool st[N];
int cnt[N];
void add(int a,int b,int c){
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
void build(int x){
memset(h,-1,sizeof h);
idx=0;
for(int i=1;i<=24;i++){
add(i-1,i,0);
add(i,i-1,-person[i]);
}
for(int i=8;i<=24;i++){
add(i-8,i,num[i]);
}
for(int i=1;i<=7;i++){
add(i+16,i,-x+num[i]);
}
add(0,24,x);
add(24,0,-x);
}
bool spfa(int x){
//判断当前的收银员人数是否足够
build(x);//建图
memset(st,false,sizeof st);
memset(dist,-0x3f,sizeof dist);
memset(cnt,0,sizeof cnt);
queue<int>q;
q.push(0);
st[0]=true;
dist[0]=0;
while(q.size()){
auto t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]<dist[t]+w[i]){
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=25)return false;
if(!st[j]){
st[j]=true;
q.push(j);
}
}
}
}
return true;
}
signed main(){
cin>>t;
while(t--){
memset(person,0,sizeof person);
for(int i=1;i<=24;i++)cin>>num[i];
cin>>n;
for(int i=1;i<=n;i++){
int x;
cin>>x;
x++;//0留给超级源点
person[x]++;
}
bool success=false;
for(int i=0;i<=n;i++){
if(spfa(i)){
success=true;
cout<<i<<endl;
break;
}
}
if(!success)cout<<"No Solution"<<endl;
}
return 0;
}
代码2:二分check+差分约束
#include<bits/stdc++.h>
using namespace std;
int t;
int n;
const int N = 30;
const int M = 100;
int e[M],ne[M],idx,w[M];
int h[N];
int num[N];
int person[N];
int dist[N];
bool st[N];
int cnt[N];
void add(int a,int b,int c){
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
void build(int x){
memset(h,-1,sizeof h);
idx=0;
for(int i=1;i<=24;i++){
add(i-1,i,0);
add(i,i-1,-person[i]);
}
for(int i=8;i<=24;i++){
add(i-8,i,num[i]);
}
for(int i=1;i<=7;i++){
add(i+16,i,-x+num[i]);
}
add(0,24,x);
add(24,0,-x);
}
bool spfa(int x){
//判断当前的收银员人数是否足够
build(x);//建图
memset(st,false,sizeof st);
memset(dist,-0x3f,sizeof dist);
memset(cnt,0,sizeof cnt);
queue<int>q;
q.push(0);
st[0]=true;
dist[0]=0;
while(q.size()){
auto t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]<dist[t]+w[i]){
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=25)return false;
if(!st[j]){
st[j]=true;
q.push(j);
}
}
}
}
return true;
}
signed main(){
cin>>t;
while(t--){
memset(person,0,sizeof person);
for(int i=1;i<=24;i++)cin>>num[i];
cin>>n;
for(int i=1;i<=n;i++){
int x;
cin>>x;
x++;//0留给超级源点
person[x]++;
}
bool success=false;
int l=0,r=n;
while(l<r){
int mid=l+r>>1;
if(spfa(mid)){
success=true;
r=mid;
}
else l=mid+1;
}
if(spfa(l))success=true;
if(success)cout<<l<<endl;
else cout<<"No Solution"<<endl;
}
return 0;
}
边栏推荐
- C Primer Plus Chapter 10, question 14 3 × 5 array
- The programmer went to bed at 12 o'clock in the middle of the night, and the leader angrily scolded: go to bed so early, you are very good at keeping fit
- [set theory] Cartesian product (concept of Cartesian product | examples of Cartesian product | properties of Cartesian product | non commutativity | non associativity | distribution law | ordered pair
- The reason why the entity class in the database is changed into hump naming
- How do you use lodash linking function- How do you chain functions using lodash?
- 金仓数据库KingbaseES 插件kdb_exists_expand
- Joint search set: the number of points in connected blocks (the number of points in a set)
- 因子选股-打分模型
- Crazy scientist
- [fxcg] inflation differences will still lead to the differentiation of monetary policies in various countries
猜你喜欢

Which Bluetooth headset is cost-effective? Four Bluetooth headsets with high cost performance are recommended
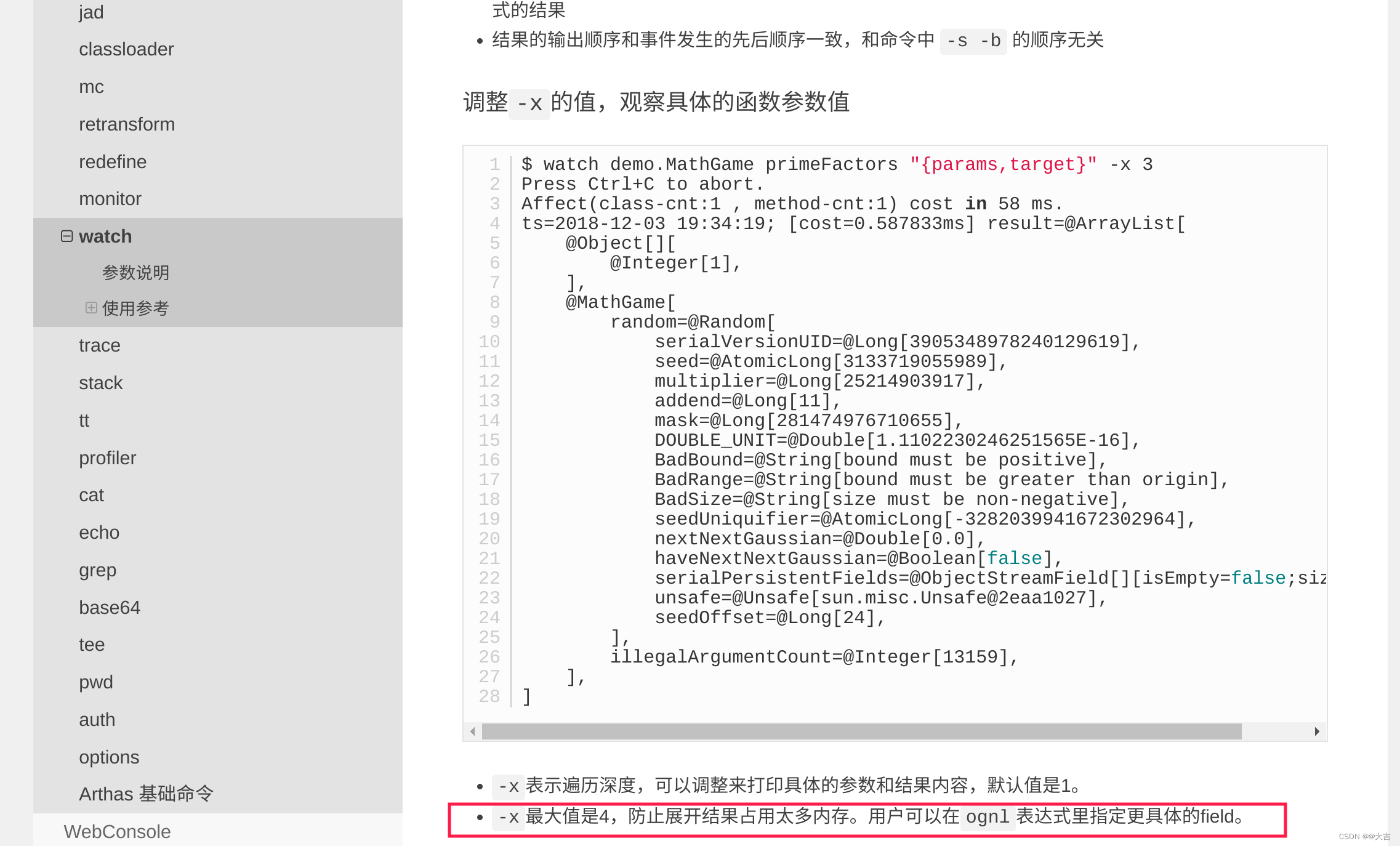
Arthas watch grabs a field / attribute of the input parameter
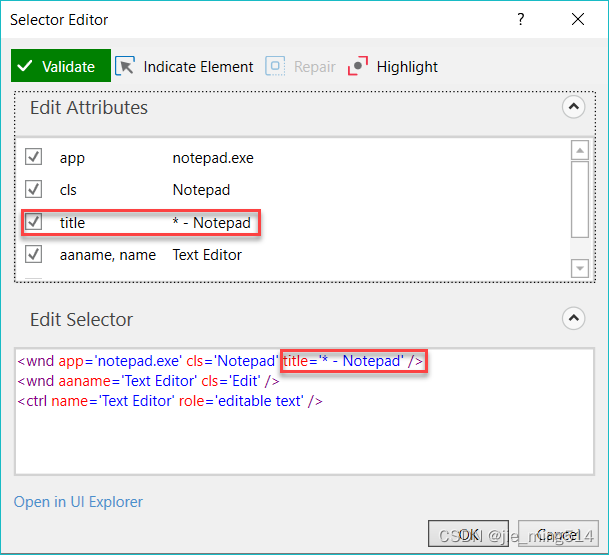
UiPath实战(08) - 选取器(Selector)

Sdl2 + OpenGL glsl practice (Continued)
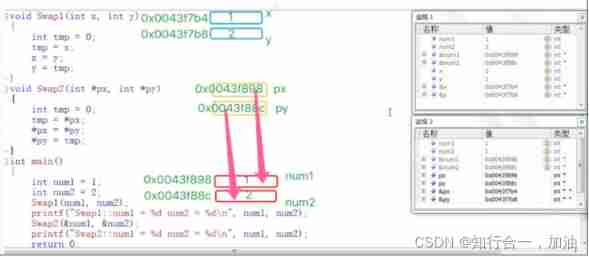
C language series - Section 3 - functions
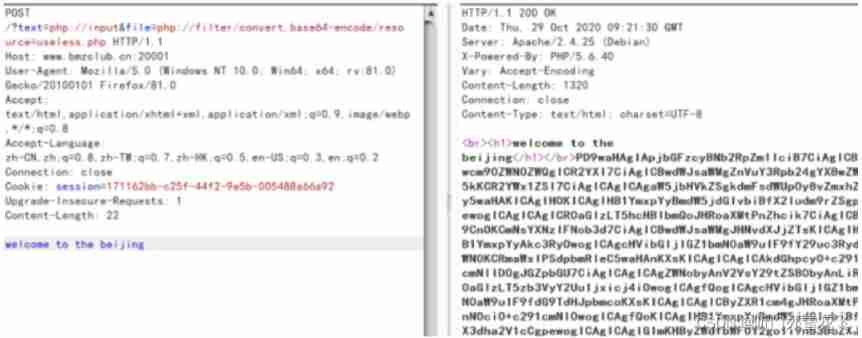
BMZCTF simple_ pop

2022 a special equipment related management (elevator) analysis and a special equipment related management (elevator) simulation test
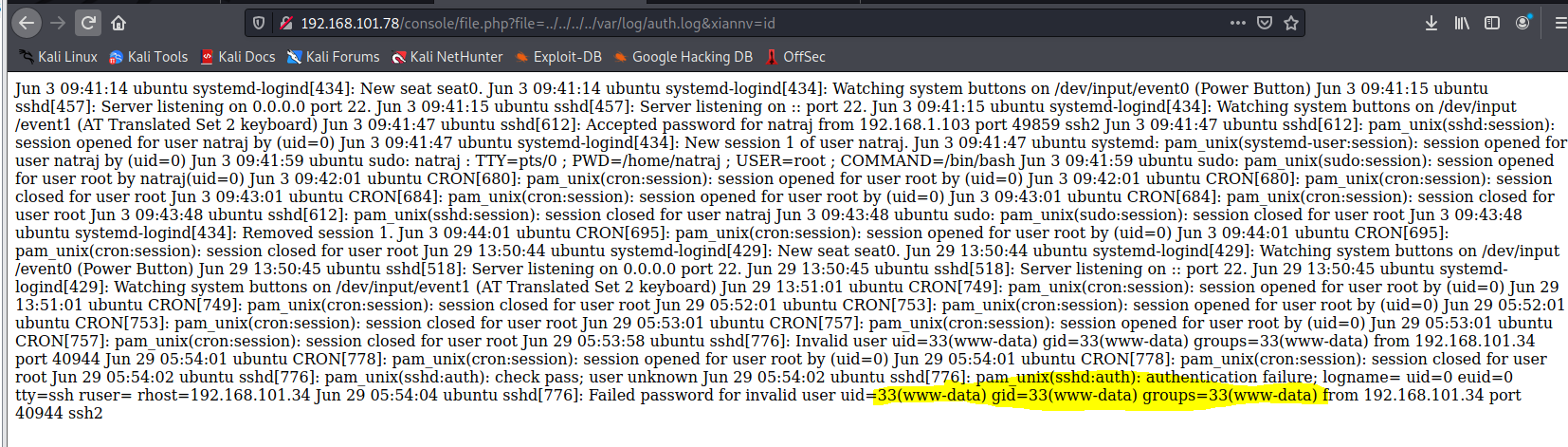
vulnhub HA: Natraj

vulnhub HA: Natraj

arthas watch 抓取入参的某个字段/属性
随机推荐
Summary of training competition (Lao Li's collection of questions)
2.14 summary
stm32逆向入门
使用BENCHMARKSQL工具对kingbasees并发测试时kill掉主进程成功后存在子线程未及时关闭
Asp access teaching management system design finished product
2022-02-13 (347. Top k high frequency elements)
Function introduction of member points mall system
Kubernetes source code analysis (I)
Factor stock selection scoring model
《牛客刷verilog》Part II Verilog进阶挑战
BMZCTF simple_ pop
金仓数据库KingbaseES 插件kdb_database_link
2022 registration of G2 utility boiler stoker examination and G2 utility boiler stoker reexamination examination
[set theory] binary relationship (special relationship type | empty relationship | identity relationship | global relationship | divisive relationship | size relationship)
Which Bluetooth headset is good about 400? Four Bluetooth headsets with strong noise reduction are recommended
MC Layer Target
金仓数据库KingbaseES 插件kdb_exists_expand
IPhone x forgot the boot password
有道云笔记
Leetcode simple question: the key with the longest key duration