leetcode-952：按公因数计算最大组件大小

题目

题目连接
给定一个由不同正整数的组成的非空数组 nums ，考虑下面的图：

有 nums.length 个节点，按从 nums[0] 到 nums[nums.length - 1] 标记；
只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时，nums[i] 和 nums[j]之间才有一条边。
返回 图中最大连通组件的大小 。

示例 1：

输入：nums = [4,6,15,35]
输出：4

示例 2：

输入：nums = [20,50,9,63]
输出：2

示例 3：

输入：nums = [2,3,6,7,4,12,21,39]
输出：8

解题

方法一：带权重有向图+并查集（超时）

带权重的图+并查集

写法一：

每个节点还带了权重weight[i]，表示直接指向当前节点的 节点个数
最后只需要找到权重最大的，就是我们想要的答案。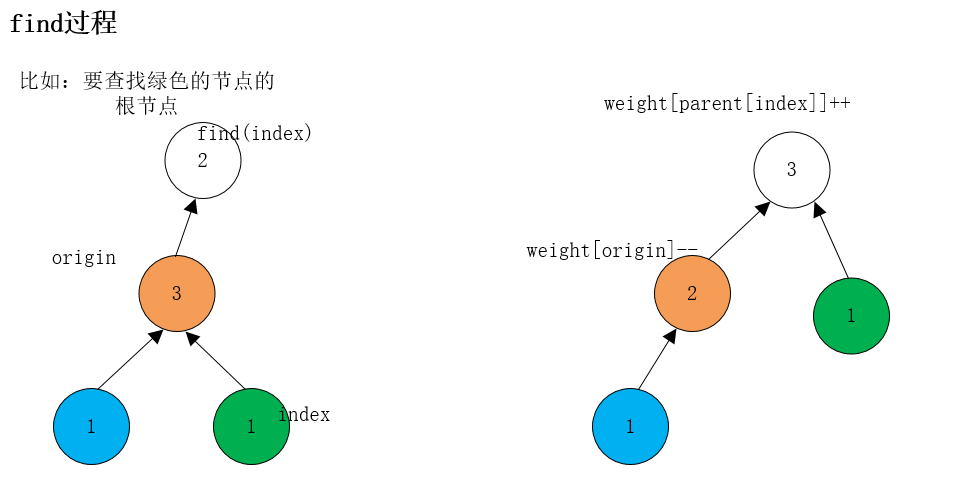

能直接遍历weight来获得最大的集合元素个数？显然不能直接这么做，还需要对他进行路径压缩，让元素直接指向根节点。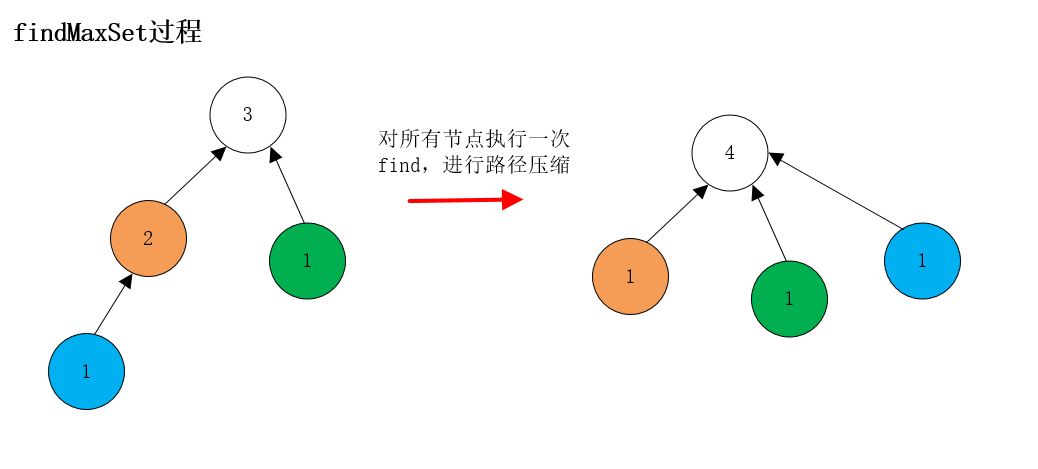

class UnionFind{
    
private:
    vector<int> parent;
    vector<int> weight;
public:
    UnionFind(int n){
    
        parent.resize(n);
        weight.resize(n);
        for(int i=0;i<n;i++){
    
            parent[i]=i;
            weight[i]=1;//直接指向当前节点的数量(包含自身，注意孙子节点，不算直接指向)
        }
    }
    int find(int index){
    
        if(parent[index]==index) return index;
        int origin=parent[index];
        parent[index]=find(parent[index]);
        weight[parent[index]]++;//指向根节点的节点数量+1
        weight[origin]--;//指向原先节点的节点数量-1
        return parent[index];
    }

    void unite(int index1,int index2){
    
        int p1=find(index1);
        int p2=find(index2);
        if(p1!=p2){
    
            parent[p1]=p2;
            weight[p2]++;//指向根节点的节点数量+1
        }
    }
    int findMaxSet(){
    
        for(int i=0;i<weight.size();i++){
    
            find(i);
        }
        int res=0;
        for(int i=0;i<weight.size();i++){
    
            res=max(res,weight[i]);
        }
        return res;
    }
};

class Solution {
    
public:
    int largestComponentSize(vector<int>& nums) {
    
        int n=nums.size();
        UnionFind uf(n);

        unordered_map<int,int> mp;
        int id=0;
        for(int i=0;i<n;i++){
    
            if(!mp.count(nums[i])){
    
                mp[nums[i]]=id++;
            }
        }

        for(int i=0;i<n;i++){
    
            for(int j=i+1;j<n;j++){
    
                int id1=mp[nums[i]];
                int id2=mp[nums[j]];
                if(gcd(nums[i],nums[j])>1){
    
                    uf.unite(id1,id2);
                }
            }
        }
        return uf.findMaxSet();
    }
};

写法二：
weight表示，指向当前节点的节点数(包含孙子节点等)
只要在unite里面加上另一个子树的所有节点 数就行了，find过程中进行的路径压缩，只是调整了指向根节点，但是该根节点的所有节点数是不会变的。

class UnionFind{
    
private:
    vector<int> parent;
    vector<int> weight;
public:
    UnionFind(int n){
    
        parent.resize(n);
        weight.resize(n);
        for(int i=0;i<n;i++){
    
            parent[i]=i;
            weight[i]=1;//指向当前节点的数量（包含孙子节点等）
        }
    }
    int find(int index){
    
        if(parent[index]==index) return index;
        parent[index]=find(parent[index]);
        return parent[index];
    }

    void unite(int index1,int index2){
    
        int p1=find(index1);
        int p2=find(index2);
        if(p1!=p2){
    
            parent[p1]=p2;
            weight[p2]+=weight[p1];//指向根节点的节点数量 加上 子树的节点数量
        }
    }
    int findMaxSet(){
    
        for(int i=0;i<weight.size();i++){
    
            find(i);
        }
        int res=0;
        for(int i=0;i<weight.size();i++){
    
            res=max(res,weight[i]);
        }
        return res;
    }
};

class Solution {
    
public:
    int largestComponentSize(vector<int>& nums) {
    
        int n=nums.size();
        UnionFind uf(n);

        unordered_map<int,int> mp;
        int id=0;
        for(int i=0;i<n;i++){
    
            if(!mp.count(nums[i])){
    
                mp[nums[i]]=id++;
            }
        }

        for(int i=0;i<n;i++){
    
            for(int j=i+1;j<n;j++){
    
                int id1=mp[nums[i]];
                int id2=mp[nums[j]];
                if(gcd(nums[i],nums[j])>1){
    
                    uf.unite(id1,id2);
                }
            }
        }
        return uf.findMaxSet();
    }
};

主要超时原因还是因为两层for循环

方法二：枚举质因数+并查集

参考链接

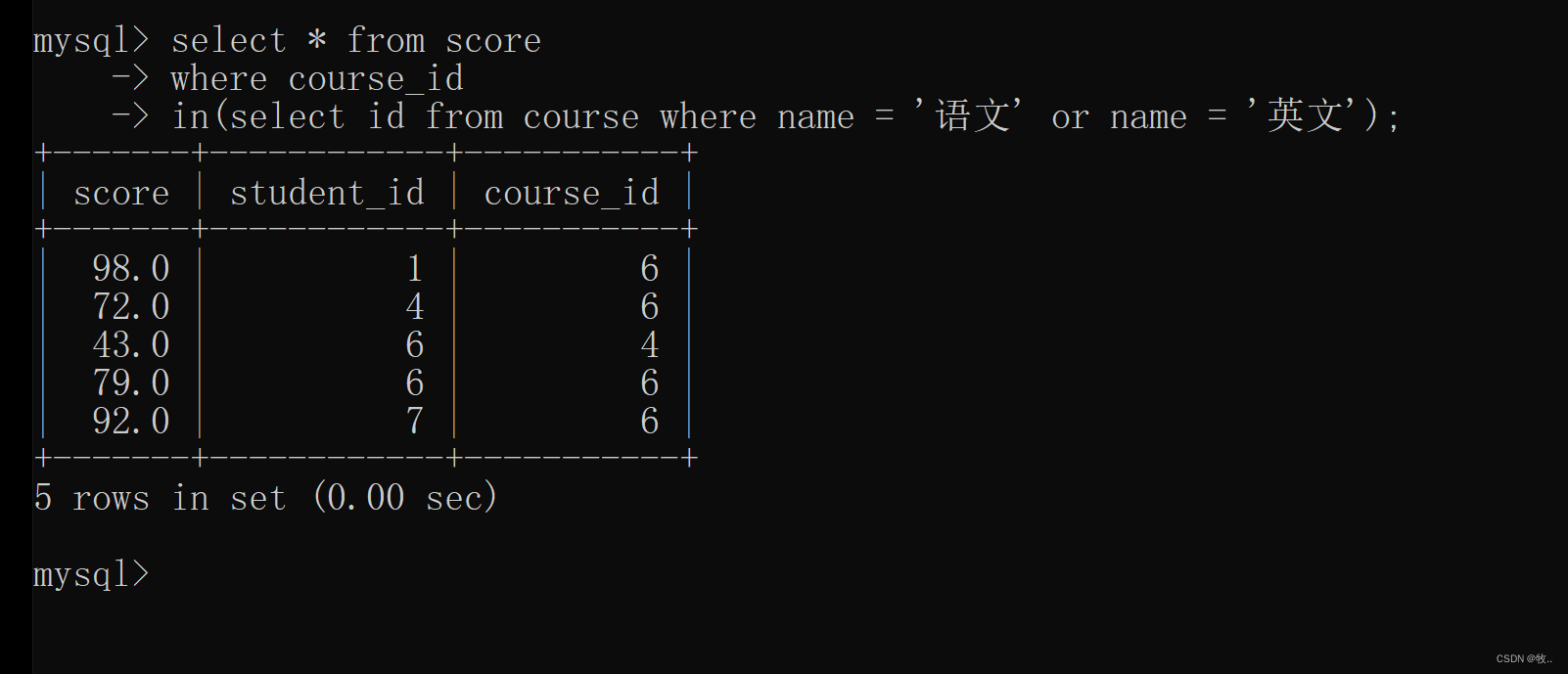
基本思路：把关联的加入到并查集中，最后遍历nums，相同的根节点那么数量+1，这样就能找到最多元素的集合了。

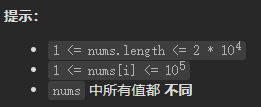
由于nums.length最大为$2\ast 10^4$lianjie
遍历每个值，两两匹配会超时。

因此采用枚举公因式的方式，如果k>=2，且num%k==0，那么k为公约数，对num和k进行联结，以及num和num/k进行联结。不管k或者num/k有没有在nums中这都不要紧，因为后面遍历nums的时候不会遍历到它们。
相比$O(4\ast 10^8)$的复杂度来的更小。

class UnionFind{
    
private:
    vector<int> parent;
public:
    UnionFind(int n){
    
        parent.resize(n);
        for(int i=0;i<n;i++){
    
            parent[i]=i;
        }
    }
    int find(int index){
    
        if(parent[index]==index) return index;
        return parent[index]=find(parent[index]);
    }

    void unite(int index1,int index2){
    
        int p1=find(index1);
        int p2=find(index2);
        if(p1==p2) return;
        parent[p1]=p2;
    }
};

class Solution {
    
public:
    int largestComponentSize(vector<int>& nums) {
    
        int maxLength=*max_element(nums.begin(),nums.end());
        int n=nums.size();
        UnionFind uf(maxLength+1);

        for(int num:nums){
    
            for(int k=sqrt(num);k>=2;k--){
    
                if(num%k==0){
    
                    uf.unite(num,k);//不管k属不属于num都没有关系，把他添加到集合中。因为后续还要遍历一遍nums
                    uf.unite(num,num/k);
                }
            }
        }
        vector<int> cnt(maxLength+1);
        int res=0;
        for(int num:nums){
    //遍历nums中的值，同一集合的+1
            cnt[uf.find(num)]++;
            res=max(res,cnt[uf.find(num)]);
        }
    
        return res;
    }
};