当前位置:网站首页>[combinatorics] generating function (example of using generating function to solve the number of solutions of indefinite equation)
[combinatorics] generating function (example of using generating function to solve the number of solutions of indefinite equation)
2022-07-03 18:04:00 【Programmer community】
List of articles
- One 、 Examples of using generating functions to solve the number of solutions of indefinite equations
Reference blog :
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
- 【 Combinatorial mathematics 】 Generating function ( Commutative properties | Derivative property | Integral properties )
- 【 Combinatorial mathematics 】 Generating function ( Summary of nature | Important generating functions ) *
- 【 Combinatorial mathematics 】 Generating function ( Generate function examples | Given the general term formula, find the generating function | Given the generating function, find the general term formula )
- 【 Combinatorial mathematics 】 Generating function ( Generate function application scenarios | Solving recursive equations using generating functions )
- 【 Combinatorial mathematics 】 Generating function ( Use the generating function to solve multiple sets r Combinatorial number )
- 【 Combinatorial mathematics 】 Generating function ( Use generating function to solve the number of solutions of indefinite equation )
One 、 Examples of using generating functions to solve the number of solutions of indefinite equations
1
1
1 Gram weight
2
2
2 individual ,
2
2
2 Gram weight
1
1
1 individual ,
4
4
4 Gram weight
2
2
2 individual ,
Which weights can be weighed , How many schemes are there ;
1
1
1 Gram's weight The number is
x
1
x_1
x1 individual , The value range is
0
≤
x
1
≤
2
0 \leq x_1 \leq 2
0≤x1≤2 , Value for
0
,
1
,
2
0 , 1, 2
0,1,2
2
2
2 The number of weights of gram is
x
2
x_2
x2 individual , The value range is
0
≤
x
2
≤
1
0 \leq x_2 \leq 1
0≤x2≤1 , Value for
0
,
1
0,1
0,1
4
4
4 The number of weights of gram is
x
3
x_3
x3 individual , The value range is
0
≤
x
3
≤
2
0 \leq x_3 \leq 2
0≤x3≤2 , Value for
0
,
1
,
2
0,1,2
0,1,2
x
1
+
2
x
2
+
4
x
3
=
r
x_1 + 2x_2 + 4x_3 = r
x1+2x2+4x3=r , among
r
r
r Represents the weight that can be weighed ,
Write the above , With restrictions , And with coefficients Of nonnegative integer solutions of indefinite equations Generating function :
x
1
x_1
x1 term , With restrictions , There is no coefficient , Its The bottom is
y
y
y , Power value
0
,
1
,
2
0 , 1, 2
0,1,2 , The corresponding generating function item is
(
1
+
y
+
y
2
)
( 1 + y + y^2 )
(1+y+y2)
x
2
x_2
x2 term , With restrictions , With coefficients
2
2
2 , Its The bottom is
y
2
y^2
y2 , Power value
0
,
1
0,1
0,1 , The corresponding generating function item is
(
y
2
)
0
+
(
y
2
)
1
=
1
+
y
2
(y^2)^0 + (y^2)^1 = 1+ y^2
(y2)0+(y2)1=1+y2
x
3
x_3
x3 term , With restrictions , With coefficients
4
4
4 , Its The bottom is
y
4
y^4
y4 , Power value
0
,
1
,
2
0,1, 2
0,1,2 , The corresponding generating function item is
(
y
4
)
0
+
(
y
4
)
1
+
(
y
4
)
2
=
1
+
y
4
+
y
8
(y^4)^0 + (y^4)^1 + (y^4)^2 = 1+ y^4 + y^8
(y4)0+(y4)1+(y4)2=1+y4+y8
Multiply the above three items , And unfold :
G
(
x
)
=
(
1
+
y
+
y
2
)
(
1
+
y
2
)
(
1
+
y
4
+
y
8
)
G(x) = ( 1 + y + y^2 ) (1+ y^2) (1+ y^4 + y^8)
G(x)=(1+y+y2)(1+y2)(1+y4+y8)
=
1
+
y
+
2
y
2
+
y
3
+
2
y
4
+
y
5
+
2
y
6
+
y
7
+
2
y
8
+
y
9
+
2
y
10
+
y
11
+
y
12
\ \ \ \ \ \ \ \ \ \ =1 + y + 2y^2 + y^3 + 2y^4 + y^5 + 2y^6 + y^7 + 2y^8 + y^9 + 2y^{10} + y^{11} + y^{12}
=1+y+2y2+y3+2y4+y5+2y6+y7+2y8+y9+2y10+y11+y12
After the above expansion
y
y
y The idempotent of is weight , The coefficient is Number of schemes , Such as
2
y
8
2y^8
2y8 Item representation , Weigh out
8
8
8 Gram weight , Yes
2
2
2 A plan ;
General description :
1
1
1 term : Express
y
0
y^0
y0 , Weigh out
0
0
0 g , Yes
0
0
0 Kind of plan ;
y
y
y term : Express
y
1
y^1
y1 , Weigh out
1
1
1 g , Yes
1
1
1 Kind of plan ;
2
y
2
2y^2
2y2 term : Express
2
y
2
2y^2
2y2 , Weigh out
2
2
2 g , Yes
2
2
2 Kind of plan ;
y
3
y^3
y3 term : Express
y
3
y^3
y3 , Weigh out
3
3
3 g , Yes
1
1
1 Kind of plan ;
2
y
4
2y^4
2y4 term : Express
2
y
4
2y^4
2y4 , Weigh out
4
4
4 g , Yes
2
2
2 Kind of plan ;
y
5
y^5
y5 term : Express
y
5
y^5
y5 , Weigh out
5
5
5 g , Yes
1
1
1 Kind of plan ;
2
y
6
2y^6
2y6 term : Express
2
y
6
2y^6
2y6 , Weigh out
6
6
6 g , Yes
2
2
2 Kind of plan ;
y
7
y^7
y7 term : Express
y
7
y^7
y7 , Weigh out
7
7
7 g , Yes
1
1
1 Kind of plan ;
2
y
8
2y^8
2y8 term : Express
2
y
8
2y^8
2y8 , Weigh out
8
8
8 g , Yes
2
2
2 Kind of plan ;
y
9
y^9
y9 term : Express
y
9
y^9
y9 , Weigh out
9
9
9 g , Yes
1
1
1 Kind of plan ;
2
y
10
2y^{10}
2y10 term : Express
2
y
10
2y^{10}
2y10 , Weigh out
10
10
10 g , Yes
2
2
2 Kind of plan ;
y
11
y^{11}
y11 term : Express
y
11
y^{11}
y11 , Weigh out
11
11
11 g , Yes
1
1
1 Kind of plan ;
y
12
y^{12}
y12 term : Express
y
12
y^{12}
y12 , Weigh out
12
12
12 g , Yes
1
1
1 Kind of plan ;
边栏推荐
- The gbase 8A database does not support the DB2 function value (column_name, 0) cluster syntax
- Automata and automatic line of non-standard design
- Redis core technology and practice - learning notes (11): why not just string
- Computer graduation design PHP makeup sales Beauty shopping mall
- The third day of writing C language by Yabo people
- Research Report on investment trends and development planning of China's thermal insulation material industry, 2022-2028
- 聊聊支付流程的設計與實現邏輯
- Servlet specification Part II
- 一入“远程”终不悔,几人欢喜几人愁。| 社区征文
- How to draw non overlapping bubble chart in MATLAB
猜你喜欢

STM32 realizes 74HC595 control
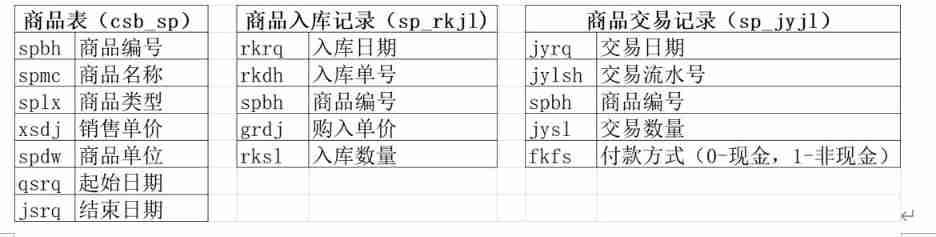
Five problems of database operation in commodity supermarket system
AcWing 271. 杨老师的照相排列【多维DP】
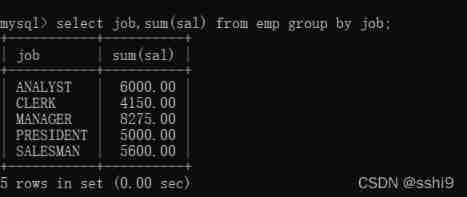
MySQL grouping query

Leetcode Valentine's Day Special - looking for a single dog
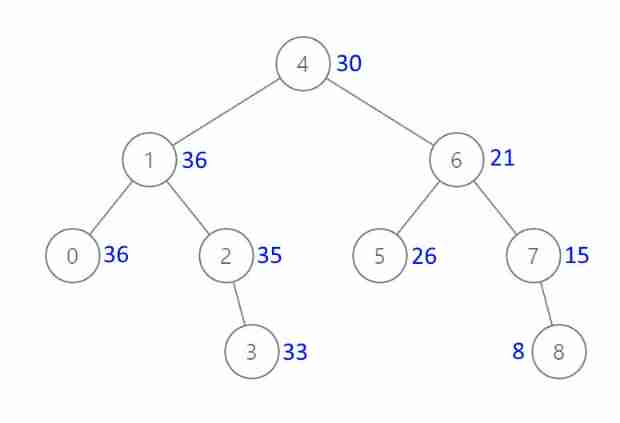
Leetcode 538 converts binary search tree into cumulative tree -- recursive method and iterative method

PHP MySQL inserts data
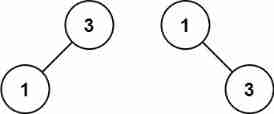
Leetcode 108 converts an ordered array into a binary search tree -- recursive method

PHP MySQL preprocessing statement
Micro service component sentinel console call
随机推荐
As soon as we enter "remote", we will never regret, and several people will be happy and several people will be sad| Community essay solicitation
Research Report on investment trends and development planning of China's thermal insulation material industry, 2022-2028
[enumeration] annoying frogs always step on my rice fields: (who is the most hateful? (POJ hundred practice 2812)
Analysis report on production and marketing demand and investment forecast of China's PVC industry from 2021 to 2026
MinGW compile boost library
How to draw non overlapping bubble chart in MATLAB
[combinatorics] generating function (linear property | product property)
The number of incremental paths in the grid graph [dfs reverse path + memory dfs]
PHP MySQL reads data
Talk about the design and implementation logic of payment process
企业级自定义表单引擎解决方案(十二)--表单规则引擎2
Supervisor monitors gearman tasks
Kotlin的协程:上下文
毕业总结
解决Zabbix用snmp监控网络流量不准的问题
Discussion sur la logique de conception et de mise en oeuvre du processus de paiement
Kotlin的協程:上下文
远程办公工具分享|社区征文
Market demand survey and marketing strategy analysis report of global and Chinese pet milk substitutes 2022-2028
TCP拥塞控制详解 | 3. 设计空间