当前位置:网站首页>Example 003: a complete square is an integer. It is a complete square after adding 100, and it is a complete square after adding 168. What is the number?
Example 003: a complete square is an integer. It is a complete square after adding 100, and it is a complete square after adding 168. What is the number?
2022-07-05 08:21:00 【Lazy smile】
example 003: Complete square
subject : An integer , It adds 100 And then there's a complete square , Plus 168 It's a complete square again , What is the number ?
Program analysis : because 168 It's too small for an exponential explosion , Therefore, mathematical analysis can be omitted directly , Use the simplest way to get the upper limit ,
n = 0
while (n + 1) ** 2 - n * n <= 168:
n += 1
print('----n=', n) # It can be concluded that the range is (n+1)**2 Inside The train of thought is :
The worst result is n The sum of the squares of (n+1) The square of is just the difference 168, Because it's Square , There can be no greater gap than this .
Let this number be i (i+100)**0.5 (i+100+168)**0.5 Then the results are all integers .
As for judging whether it is a complete square number , The easiest way is : The value of the square root is decimal 0 that will do .
for i in range((n + 1) ** 2):
if i ** 0.5 == int(i ** 0.5) and (i + 168) ** 0.5 == int((i + 168) ** 0.5):
print(i - 100)The combination is :
# The worst result is n The sum of the squares of (n+1) The square of is just the difference 168, There can be no greater gap than this , Based on this, we come to the conclusion that n
n = 0
while (n + 1) ** 2 - n * n <= 168:
n += 1
print('----n=', n) # It can be concluded that the range is (n+1)**2 Inside
for i in range((n + 1) ** 2):
if i ** 0.5 == int(i ** 0.5) and (i + 168) ** 0.5 == int((i + 168) ** 0.5):
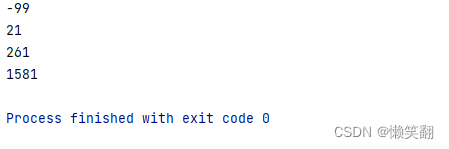
print(i - 100)------n= 84
-99
21
261
1581Therefore, the number can be :-99 21 61 1581
边栏推荐
- [tutorial 15 of trio basic from introduction to proficiency] trio free serial communication
- C WinForm [help interface - send email] - practice five
- Sql Server的存储过程详解
- 动力电池UL2580测试项目包括哪些
- Ble encryption details
- Brief discussion on Buck buck circuit
- Keil use details -- magic wand
- Void* C is a carrier for realizing polymorphism
- 【三层架构】
- Various types of questions judged by prime numbers within 100 (C language)
猜你喜欢
![[trio basic tutorial 16 from introduction to proficiency] UDP communication test supplement](/img/54/78e4e10724b2762274b06debb10877.jpg)
[trio basic tutorial 16 from introduction to proficiency] UDP communication test supplement
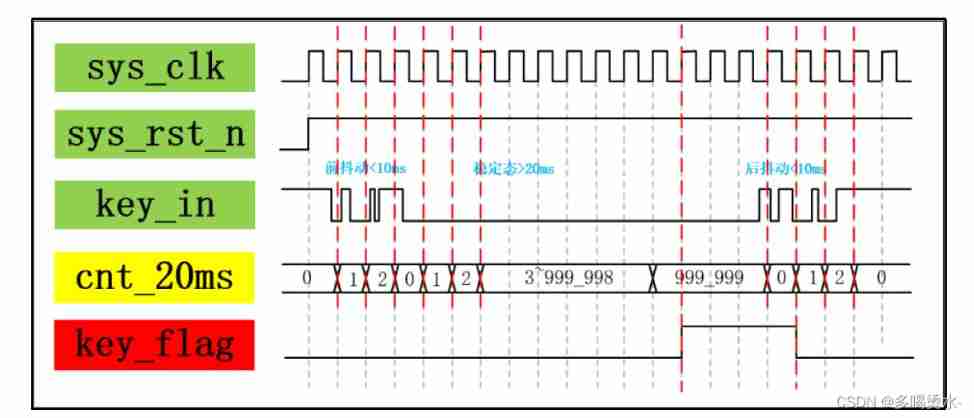
Hardware and software solution of FPGA key chattering elimination
Matlab2018b problem solving when installing embedded coder support package for stmicroelectronic
Working principle and type selection of common mode inductor
![C WinForm [exit application] - practice 3](/img/25/30c795cc3fa6931eb1d733719d4ad0.jpg)
C WinForm [exit application] - practice 3
Arduino uses nrf24l01+ communication
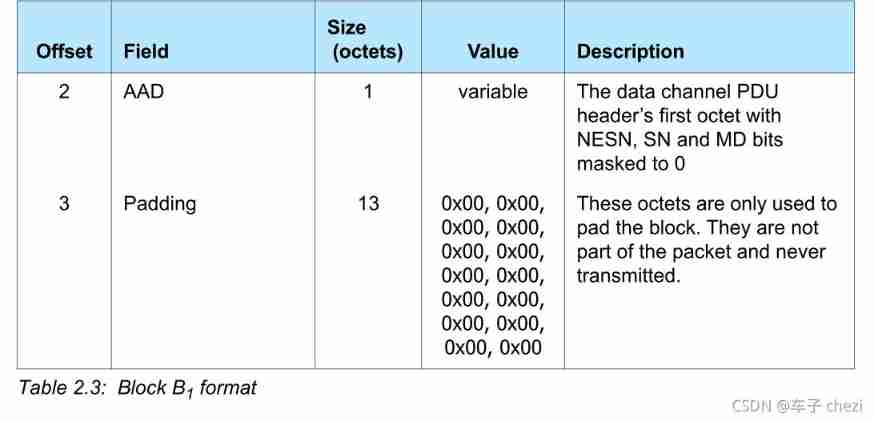
Ble encryption details
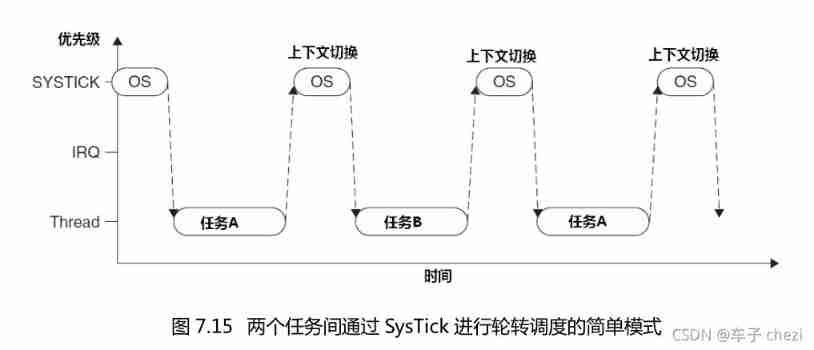
Explain task scheduling based on Cortex-M3 in detail (Part 1)
OC and OD gate circuit
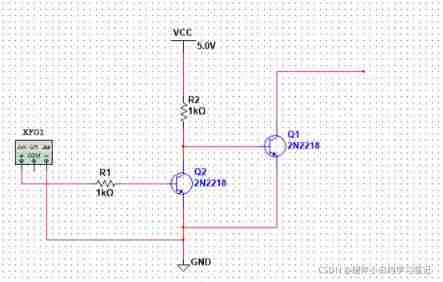
Classic application of MOS transistor circuit design (1) -iic bidirectional level shift
随机推荐
Hardware and software solution of FPGA key chattering elimination
STM32 --- NVIC interrupt
DokuWiki deployment notes
OC and OD gate circuit
Sizeof (function name) =?
动力电池UL2580测试项目包括哪些
More than 90% of hardware engineers will encounter problems when MOS tubes are burned out!
Explain task scheduling based on Cortex-M3 in detail (Part 2)
H264 (I) i/p/b frame gop/idr/ and other parameters
Shell script realizes the reading of serial port and the parsing of message
STM32 single chip microcomputer -- volatile keyword
Step motor generates S-curve upper computer
Imx6ull bare metal development learning 1-assembly lit LED
[tutorial 15 of trio basic from introduction to proficiency] trio free serial communication
【论文阅读】2022年最新迁移学习综述笔注(Transferability in Deep Learning: A Survey)
Correlation based template matching based on Halcon learning [II] find_ ncc_ model_ defocused_ precision. hdev
Negative pressure generation of buck-boost circuit
PMSM dead time compensation
实例006:斐波那契数列
Shape template matching based on Halcon learning [9] PM_ multiple_ dxf_ models. Hdev routine -- [read and write XLD from DXF file]