Cache penetration tool "Bloom filter"

BitMap

Modern computers use binary （bit, position ） As the basic unit of information ,1  Bytes are equal to  8  position , for example

big

Strings are created by  3  Byte composition , But it is actually represented in binary when stored in the computer ,

big

Respectively corresponding  ASCII  The codes are  98、105、103, The corresponding binaries are  01100010、01101001  and  01100111.

Many development languages provide the function of operation bits , Reasonable use of bits can effectively improve memory utilization and development efficiency .

Bit-map  The basic idea is to use one  bit  Bit to mark the corresponding  value, and  key  That's the element . Because of the adoption of  bit  Store data in units , So in terms of storage space , Can save a lot .

stay  Java  in ,int  Occupy  4  byte ,1  byte  = 8 position （1 byte = 8 bit）, If we use this  32  individual  bit  If the value of each bit of a bit represents a number, can it represent  32  A digital , in other words  32  Only one number is needed  int  The space occupied is enough , Then you can reduce the space  32  times .

1 Byte = 8 Bit,1 KB = 1024 Byte,1 MB = 1024 KB,1GB = 1024 MB

Suppose the website has  1  Billion users , The users who visit independently every day are  5  Ten million , If you use set type and  BitMap  Store active users separately ：

• If the user  id  yes  int  type ,4  byte ,32  position , The space occupied by the collection type is  50 000 000 * 4/1024/1024 = 200M;

• If stored by bit ,5  Tens of millions is  5  Thousands of people , The space occupied is  50 000 000/8/1024/1024 = 6M.

So how to use  BitMap  To represent a number ？

It says use  bit  Bit to mark the corresponding  value, and  key  That's the element , We can  BitMap  Think of it as a bit

Array

, Each unit of an array can only store  0  and  1（0  Indicates that this number does not exist ,1  Indicates presence ）, The subscript of the array is in  BitMap  It's called offset . For example, we need to express

{1,3,5,7}

The number four , as follows ：

If there is a number  65  Well ？ Just drive

int[N/32+1]

individual  int  The array can store all this data （ among  N  Represents the maximum value in this group of data ）, namely ：

int[0]： Can be said  0~31

int[1]： Can be said  32~63

int[2]： Can be said  64~95

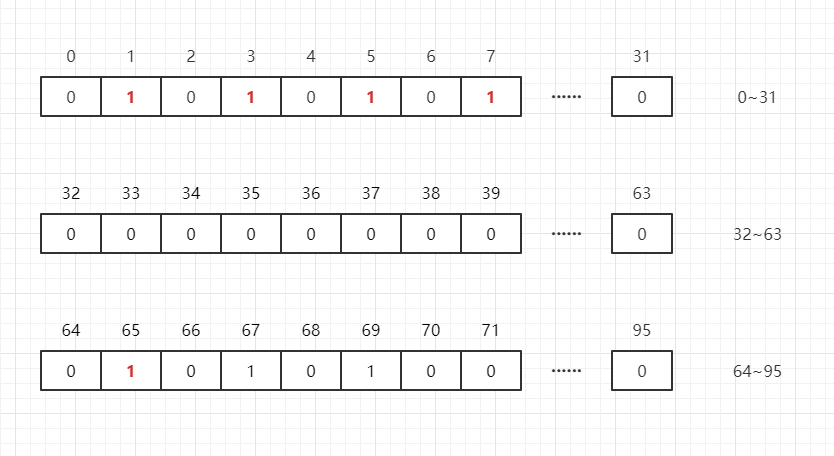
Suppose we want to determine whether any integer is in the list , be  

M/32

  You get the subscript ,

M%32

I know where it is in this subscript , Such as ：

65/32 = 2

,

65%32=1

, namely  65  stay

int[2]

  No  1  position .

The bloon filter

In essence, the bloom filter is a data structure , A more ingenious probabilistic data structure , Features efficient insertion and query , It can be used to tell you  “ some   Something must or may not exist ”.

Compared to traditional  List、Set、Map  And so on , It's more efficient 、 Take up less space , But the disadvantage is that the returned result is probabilistic , Not exactly .

actually , Bloom filters are widely used in

Web blacklist system

、

Spam filtering system

、

Crawler website weight judgment system

etc. ,Google  Famous distributed database  Bigtable  Used a bloom filter to find non-existent rows or columns , To reduce the number of disk lookups  IO  frequency ,Google Chrome  Browser uses bloom filter to speed up safe browsing service .

In many  Key-Value  The system also uses the bloom filter to speed up the query process , Such as  Hbase,Accumulo,Leveldb, generally speaking ,Value  Save on disk , It takes a lot of time to access the disk , However, using a bloom filter can quickly determine a certain  Key  Corresponding  Value  Whether there is , So you can avoid a lot of unnecessary disks  IO  operation .

Through one  Hash  Function maps an element to a bit array （Bit Array） A point in . thus , We just need to see if this point is  1  We'll know if it's in the set . This is the basic idea of bloon filter .

Use scenarios

1、 There are  10  A natural number of billion , To arrange in disorder , It needs to be sorted . The limit is  32  It's done on the machine , Memory is limited to  2G. How to complete ？

2、 How to quickly locate in the 100 million blacklist  URL  Whether the address is on the blacklist ？( Every one of them  URL  Average  64  byte )

3、 User login behavior analysis is required , To determine the user's activity ？

4、 Web crawler - How to determine  URL  Has it been climbed ？

5、 Quickly locate user attributes （ The blacklist 、 White list, etc ）？

6、 Data is stored on disk , How to avoid a large number of invalid  IO？

7、 To judge whether an element exists in billion level data ？

8、 Cache penetration .

Shortcomings of traditional data structures

Generally speaking , Page  URL  Save it into the database for search , Or create a hash table to look it up  OK  了 .

When the amount of data is small , It's right to think so , You can actually map values to  HashMap  Of  Key, Then you can go to  O(1)  Within the time complexity of   Return results , Extremely efficient . however  HashMap  The implementation also has disadvantages , For example, the proportion of storage capacity is high , Considering the existence of load factor , Usually space cannot be used up , For example, if a  1000  ten thousand  HashMap,Key=String（ Length not exceeding  16  character , With minimal repeatability ）,Value=Integer, How much space will it take ？1.2  individual  G.

In fact, it uses  bitmap,1000  m  int  type , It only needs  40M（ 10 000 000 * 4/1024/1024 =40M） Left and right space , Proportion  3%,1000  m  Integer, need  161M  Left and right space , Proportion  13.3%.

It can be seen that once you are worth a lot, such as hundreds of millions , that  HashMap  The amount of memory occupied can be imagined .

But if the whole web blacklist system contains  100  Hundreds of millions of web pages  URL, Searching in the database is time-consuming , And if each  URL  Space for  64B, Then the required memory is  640GB, It is difficult for ordinary servers to meet this demand .

Realization principle

Suppose we have a set  A,A  There is  n  Elements . utilize

k A hash hash

function , take A Every element in

mapping

To a length of  a  Bit array  B At different locations in , Binary numbers at these locations are set to  1. If the element to be checked , Through here  k After the mapping of a hash function , Found that the  k  Binary numbers in two positions

All for  1

, This element probably belongs to the collection A, conversely ,

It must not belong to the set A

.

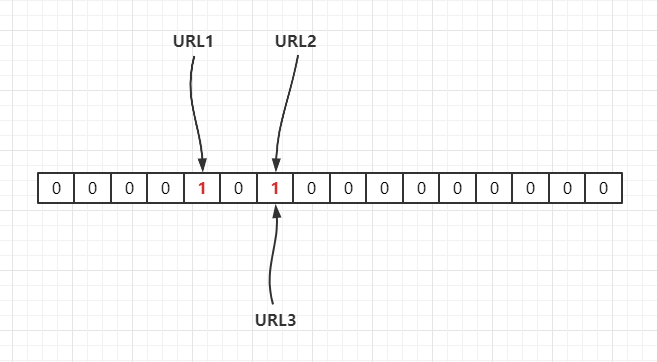
For example, we have  3  individual  URL 

{URL1,URL2,URL3}

, Through one hash  The function maps them to a length of  16  On the array of , as follows ：

If the current hash function is  

Hash1()

, Map to the array through hash operation , hypothesis

Hash1(URL1) = 3

,

Hash1(URL2) = 6

,

Hash1(URL3) = 6

, as follows ：

therefore , If we need to judge

URL1

Whether in this collection , Through

Hash(1)

Calculate its subscript , If its value is  1  It means that there is .

because  Hash  Hash conflict exists , Like above

URL2,URL3

All in one place , hypothesis  Hash  The function is good , If our array length is  m  A little bit , So if we want to reduce the conflict rate to, for example  

1%

,  This hash table can only hold  

m/100

  Elements , Obviously, the space utilization rate becomes low , That is, you can't do

Space is effective

（space-efficient）.

The solution is simple , Multiple is the use of  Hash  Algorithm , If one of them says that the element is not in the set , It must not be , as follows ：

Hash1(URL1) = 3,Hash2(URL1) = 5,Hash3(URL1) = 6

Hash1(URL2) = 5,Hash2(URL2) = 8,Hash3(URL2) = 14

Hash1(URL3) = 4,Hash2(URL3) = 7,Hash3(URL3) = 10

The above is the practice of Bloom filter , Used

k Hash functions

, Each string is followed by  k  individual  bit  Corresponding , So it reduces the probability of conflict .

Misjudgment phenomenon

The above approach also has problems , Because as the value increases, more and more , Be set to  1  Of  bit  More and more , In this way, even if a value has not been stored , But in case the hash function returns three  bit  Bits are set by other values  1 , Then the program will still judge that this value exists . For example, a nonexistent  

URL1000

, After hashing , Find out  bit  Bit down ：

Hash1(URL1000) = 7,Hash2(URL1000) = 8,Hash3(URL1000) = 14

But these above  bit  Bit has been

URL1,URL2,URL3

Set as  1  了 , At this point, the program will judge  

URL1000

  The value is .

This is the misjudgment of Bloom filter , therefore ,

The bloom filter judges that the existing does not necessarily exist , however , Judge that what does not exist must not exist .

Bloom filter can accurately represent a set , It can accurately determine whether an element is in this set , The accuracy is determined by the user's specific design , achieve  100%  It's impossible to be right . But the advantage of the bloom filter is ,

High accuracy can be achieved by using very little space

.

Realization

Redis  Of  bitmap

be based on redis  Of  bitmap Data structure to execute .

RedisBloom

The bloom filter can be used  Redis  Bitmap in (bitmap) Operation implementation , until  Redis4.0  This version provides plug-in functions ,Redis  The officially provided bloom filter was officially launched , The bloom filter is loaded as a plug-in to  Redis Server  in , The official website recommends one  RedisBloom  As  Redis  Of the bloom filter  Module.

Detailed installation 、 Instruction operation reference ：https://github.com/RedisBloom/RedisBloom

Document address ：https://oss.redislabs.com/redisbloom/

Guava  Of  BloomFilter

Guava  Project release 11.0 when , One of the new features is BloomFilter class .

Reference resources ：https://blog.csdn.net/dnc8371/article/details/106705929

Redisson

Redisson  The bottom layer implements a bloom filter based on bitmap .

public static void main(String[] args) {
 Config config = new Config();
 //  Stand alone environment
 config.useSingleServer().setAddress("redis://192.168.153.128:6379");
 // structure Redisson
 RedissonClient redisson = Redisson.create(config);
 RBloomFilter<String> bloomFilter = redisson.getBloomFilter(&quot;nameList&quot;);
 // Initialize the bloon filter ： The expected element is 100000000L, The error rate is 3%, Based on these two parameters, the bottom level will be calculated  bit  Array size
 bloomFilter.tryInit(100000L, 0.03);
 // take  10086  Insert it into the bloon filter
 bloomFilter.add(&quot;10086&quot;);
 // Determine whether the following numbers are in the bloom filter
 System.out.println(bloomFilter.contains(&quot;10086&quot;));//true
 System.out.println(bloomFilter.contains(&quot;10010&quot;));//false
 System.out.println(bloomFilter.contains(&quot;10000&quot;));//false
}

Solve cache penetration

Cache penetration refers to a fundamental query

Nonexistent data

, Neither the cache tier nor the storage tier will hit , If no data can be found from the storage layer, it will not be written to the cache layer .

Cache penetration will cause non-existent data to be queried in the storage layer every time it is requested , Lost the significance of cache protection back-end storage . Cache penetration issues can make

The back-end storage load increases

, Because many back-end storage does not have high concurrency , It may even cause the back-end storage to go down .

So we can use bloom filter to solve , Before accessing the cache layer and storage layer , There will be  key  Save in advance with a bloom filter , Do the first level intercept .

for example ： A recommendation system has  4  Billion users  id, Every hour, the algorithm engineer will calculate the recommended data according to each user's previous historical behavior and put it into the storage layer , But the latest users have no historical behavior , There will be cache penetration behavior , For this reason, users of all recommended data can be made into Bloom filters . If the bloom filter thinks that the user  id  non-existent , Then there is no access to the storage tier , It protects the storage layer to a certain extent .

notes ：

The bloom filter may misjudge , Let go of some requests , When it doesn't affect the whole , So at present, this scheme is the best scheme to deal with such problems

Reference resources ：

https://juejin.cn/post/7000159119059451941

https://www.cnblogs.com/cjsblog/p/11613708.html