Information theory and coding

Information theory studies the measurement of information , The content mainly focuses on Shannon's three theorems , The limit value of information transmission rate without distortion is studied , And the limit value of information rate under the condition that the information source is given and certain distortion is allowed , It also studies how to make the best use of the transmission capacity of the channel when the bit error rate is less than the given value .
Coding is the feasible direction pointed out by Shannon , A discipline developed to seek effective and reliable compilation methods , This paper mainly studies various feasible coding schemes and implementation techniques in noisy channels .

Information theory

• What is the message ?
  Information is an increase in certainty , Measurement of information ( entropy ) It is a measure of information uncertainty .
• Digital communication system
  Digital communication system source 、 Source and channel encoder 、 channel 、 Source and channel decoder 、 Shinjuku consists of five parts ;
  The source encoder converts the source symbols into symbols suitable for channel transmission , And compress the redundancy of the source to improve the effectiveness of communication , Also called compression coding ;
  The channel encoder improves the reliability of communication by adding redundant error correction symbols , Cooperate with decoding to reduce the error rate to the allowable range .

1. Source

• The mathematical model of the source is a sample space and a probability measure .
• Sources are divided into discrete and continuous 、 Having no memory and having memory . Discrete memoryless single symbol source only outputs one discrete symbol message at a time , Symbols at different times are statistically independent of each other ; The message output from the discrete memoryless extended source is a symbol sequence composed of many symbols sent at different times , Successively issued symbols are statistically independent of each other , The probability of a symbol sequence is the product of the probabilities of each symbol in the sequence ; There is a dependency between messages sent out successively in time by a memory source .

2. channel

• The mathematical model of the channel is described by transition probability .
• Channels are divided into discrete and continuous 、 Having no memory and having memory . Discrete memoryless single symbol channel (DMC) The input and output of are discrete single symbols without memory , Discrete memoryless N The input and output of the dimensional expansion channel are all N The symbol sequence of , The channel transition probability of the sequence corresponds to N Product of symbol channel transition probabilities .
• Four common DMC: Binary symmetric channel , Interference free channel , Binary delete channel , binary Z channel .

3. Measurement of information

Self information

• Self information ( The amount of information ):​​​​​​
  
• Conditional self information : Received yj After the xi The uncertainty of whether it happens :
  q(xi) For a priori probability ,q(xi|yj) It's a posterior probability .

Mutual information

• Mutual information : event x,y The mutual information between them is y What happens is about x The amount of information , be equal to “x The amount of self information ” subtract “y Under the condition of x The amount of self information ”:
  
• The nature of mutual information
  reciprocity : I(x;y)=I(y;x);
  Negativity : yj The occurrence of xi The possibility of happening ;
  When xi,yj Statistical independence , The mutual information quantity and conditional mutual information quantity are 0;
  The mutual information of any two events is not greater than the self information of one event .

Information entropy

• Average self information ( entropy , Source entropy ):

• Average conditional self information ( Conditional entropy ):
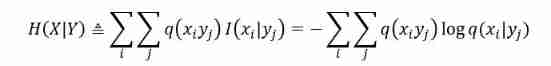
  joint probability q(xiyj)=q(yj|xi)q(xi)=q(xi|yj)q(yj); When X and Y Statistical independence ,q(xiyj)=q(xi)q(yj).

• Joint entropy :H(X) In two dimensions XY On the promotion of
  

• Average mutual information ( Interaction entropy ):
  

• entropy , Conditional entropy , The relation of joint entropy :
  
  When X,Y Statistical independence :
  

• Interaction entropy and source entropy , The relation of conditional entropy :
  

Properties of entropy function

• Extremum ( Maximum discrete entropy theorem )： For a finite set of discrete random variables , When the events in the set occur with equal probability , Entropy is maximum .
• Conditional entropy is less than or equal to unconditional entropy : H(Y|X) ≤ H(Y);
• The joint entropy is greater than the entropy of the independent event , Less than or equal to the sum of the entropy of two independent events :H(XY)>=H(X),H(XY)>=H(Y),H(XY)<=H(X)+H(Y).

Average mutual information property

• non-negative :I(X;Y)>=0;
• reciprocity :I(X;Y)=I(Y;X);
• extremum :I(X;Y)<=H(X),I(X;Y)<=H(Y);
• Concavity and convexity : Average mutual information I(X;Y) It's the source n Convex function , It's a channel u Type convex function .

4. Source code

Lossless coding does not change the entropy of the source .
Classification of codes
Source coding can be regarded as source symbol set ( news ) A mapping to a set of code symbols , A codeword is a combination of code symbols ; Only uniquely decodable is discussed in the course ( Uniquely decodable and error free coding ).

• Binary code : The code symbol set is 0,1;

• Equal length code / Variable length code : Are uniquely decodable ;

• Strange code / Nonsingular code : Different messages of nonsingular codes correspond to different codewords ;

• Original code N Secondary expansion code : Put the source N A new source symbol sequence is obtained by second extension, and a new code is obtained by concatenation of the original code ;

• The only decoding : arbitrarily N The sub extended codes are all nonsingular codes ;
  The shortest average code length among all the decoded codes is called the best code , Source coding is to find the best code .
  Kraft inequality :

• Instant code : Any code word is not the code of the prefix of other code words ( Also known as no prefix code );
  The real-time code must be the only one that can be decoded ; Real time codes can be constructed by tree graph method
  

Information transmission rate

• Average code length :
• Information transmission rate :
• Coding efficiency :

Equal length coding theorem and variable length coding theorem

• Equal length coding theorem
  
• Variable length coding theorem ( Shannon's first theorem )

Three common variable length coding methods

• Shannon coding , FeNO coding , Huffman coding ( The coding efficiency is the highest )

5. Fundamentals of channel coding

Channel coding is the processing and transformation to resist channel interference and improve reliability , Such as error control code , The simplest is " Repeat encoding , Multiple choice decoding ".
Channel capacity

I(X;Y) Is the average amount of information per symbol , For undisturbed channels, there are I(X;Y)=H(X); Channel capacity C It is to ensure the maximum information transmission capacity that the channel can accommodate under reliable communication , For fixed channels , Channel capacity is a fixed value ; To achieve channel capacity , Source distribution ( Channel input probability ) Certain conditions must be met .

• One dimensional channel and N Dimensional channel relations :
  When both the source and the channel are discrete without memory , The equal sign is established , namely N The problem of dimensional sequence transmission can be reduced to the problem of single symbol transmission .
• The channel capacity of several special channels and the necessary and sufficient conditions for reaching the channel capacity :
  
  Symmetric channels / Quasi symmetric channel / Strongly symmetric channel : A little .

Channel coding theorem ( Shannon's second theorem )

• Maximum a posteriori decoding criterion : The minimum error probability is equal to the maximum a posteriori probability .
  I will receive yi After all x Choose to make a posteriori probability q(x|y)( Also known as channel ambiguity ) maximal xi As decoding .
• Maximum likelihood decoding criterion : received yi After all x Choose to make the transition probability q(y|x) maximal xi As decoding .
• Channel coding theorem : For any discrete memoryless channel DMC, When the information transmission rate of the channel R<C, Code length N Long enough , The decoding rule can always be found to make the minimum average error decoding probability at the channel output Pmin Reach any small ( Channel capacity C Is the information transmission rate in error free transmission R The limit value of ).
• Inverse theorem of channel coding : When R>C There is no way to make the error rate arbitrarily small ( Or go to zero ).

Rate distortion coding theorem ( Shannon's third Theorem )

• Distortion measure d(x,y): Quantization distortion .
• Average distortion : Distorted mathematical expectations .
• Distortion function :
• Properties of rate distortion function
  range :
  Domain of definition :
  R(D) It's continuous , monotonous , Decreasing function .
• Rate distortion coding theorem : Given allowable distortion D, When the information transmission rate R>R(D) when , As long as the source sequence is long enough , A coding method can always be found to make the average distortion approach D.