当前位置:网站首页>机械臂速成小指南(十八):圆弧规划
机械臂速成小指南(十八):圆弧规划
2022-08-02 15:10:00 【躺躺我啊】
🥰🥳需要机械臂相关资源的同学可以在评论区中留言哦
指南目录:
机械臂速成小指南(十八):圆弧规划
🦾🪐以下为正文🦾🪐
上一篇文章中,我们介绍了直线规划,而圆弧规划也是机械臂实际作业中常用的一种笛卡尔空间轨迹规划方法。
一、理论分析
1.圆心的求解方法
对于机械臂末端的姿态插补方法与直线规划中所述方法一致,因此,今天我们主要介绍圆弧规划中对于机械臂末端的位置插补。
设![]() 分别为圆弧轨迹的起始点,中间点与目标点,连接三点可构成轨迹所在圆的内接三角形,如下图所示。
分别为圆弧轨迹的起始点,中间点与目标点,连接三点可构成轨迹所在圆的内接三角形,如下图所示。
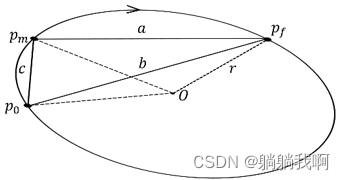
其中,a、b、c 为内接三角形的三边边长,可利用空间中两点间距离公式sqrt((x1-x2)^2+(y1-y2)^2)得到。
设l 为轨迹圆的半周长,即(a+b+c)/2 ,则轨迹圆的半径可表示为
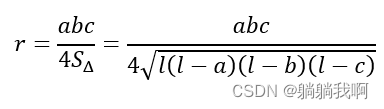
我们设圆心的坐标为O(x,y,z),则满足
![]()
以及
![]()
对上述几个式子整理,可以得到(后文需要用到)
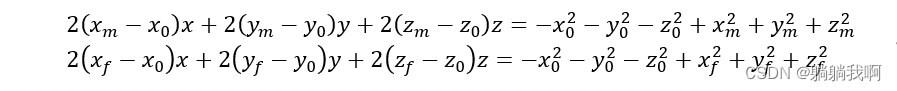
同时,设轨迹圆所在平面方程为
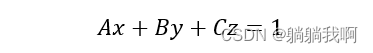
且平面方程的三个参数可由下式求得(表示为矩阵形式)。
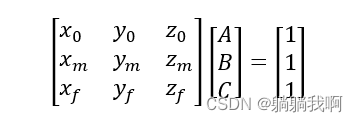
进而将式1与式2同样转为矩阵形式,表示为
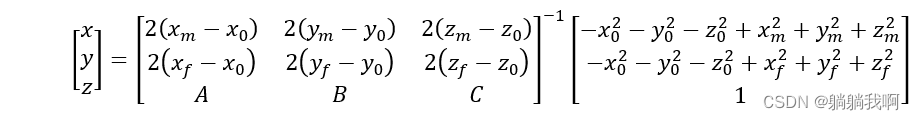
此时,通过矩阵运算即可求得圆心坐标。
2.轨迹点的生成
假设我们生成n 个轨迹点,并将圆弧的角度θ 分为n 份,第i 个轨迹点与起始点p_0 所形成弧线的角度为
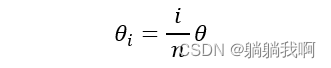
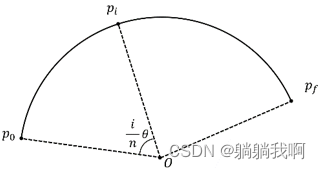
轨迹点i 的位置如下图所示。
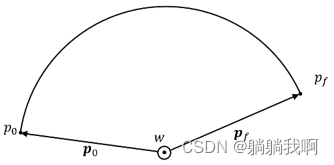
我们将轨迹点i 看作由末端执行器从p_0出发,绕经过圆心O且垂直于轨迹平面的轴旋转θ_i 得到的,旋转轴w如下图所示。
与旋转轴同向的单位向量可表示为
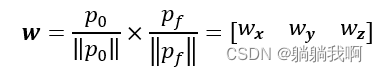
描述该变化过程的旋转矩阵可表示为
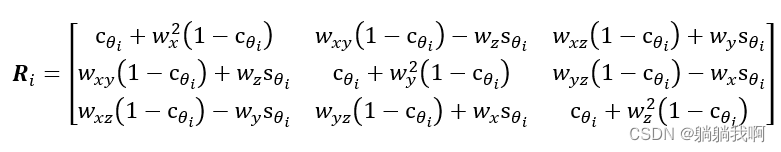
其中,![]() ,
,![]() ,其他同理。
,其他同理。
二、MATLAB程序仿真
 |  |
参照上述方法,使用MATLAB对其仿真。为便于观察轨迹形状,选择轨迹起始点(230,60,320)、轨迹中间点(230,60,400)以及轨迹终止点(230,200,410)。
第一步,定义机械臂的DH参数
N = 6;%自由度为6
radian1 = pi/180;
%定义关节角度限制
lim1_min = -170 * radian1; lim1_max = 170 * radian1; %关节1(-170,170)
lim2_min = -132 * radian1; lim2_max = 0 * radian1; %关节2(-132,0)
lim3_min = 1 * radian1; lim3_max = 141 * radian1; %关节3(1,141)
lim4_min = -165 * radian1; lim4_max = 165 * radian1; %关节4(-165,165)
lim5_min = -105 * radian1; lim5_max = 105 * radian1; %关节5(-105,105)
lim6_min = -155 * radian1; lim6_max = 155 * radian1; %关节6(-155,155)
%定义关节旋转范围
lim1 = lim1_max - lim1_min;
lim2 = lim2_max - lim2_min;
lim3 = lim3_max - lim3_min;
lim4 = lim4_max - lim4_min;
lim5 = lim5_max - lim5_min;
lim6 = lim6_max - lim6_min;
%D-H参数表
theta1 = 0; d1 = 169.77; a1 = 64.2; alpha1 = -pi/2; offset1 = 0;
theta2 = 0; d2 = 0; a2 = 305; alpha2 = 0; offset2 = 0;
theta3 = 0; d3 = 0; a3 = 0; alpha3 = pi/2; offset3 = pi/2;
theta4 = 0; d4 = -222.63; a4 = 0; alpha4 = -pi/2; offset4 = 0;
theta5 = 0; d5 = 0; a5 = 0; alpha5 = pi/2; offset5 = 0;
theta6 = 0; d6 = -36.25; a6 = 0; alpha6 = 0; offset6 = -pi;第二步,对机械臂进行运动学建模
L(1) = Link([theta1, d1, a1, alpha1, offset1], 'standard');
L(2) = Link([theta2, d2, a2, alpha2, offset2], 'standard');
L(3) = Link([theta3, d3, a3, alpha3, offset3], 'standard');
L(4) = Link([theta4, d4, a4, alpha4, offset4], 'standard');
L(5) = Link([theta5, d5, a5, alpha5, offset5], 'standard');
L(6) = Link([theta6, d6, a6, alpha6, offset6], 'standard');
% 定义关节范围
L(1).qlim=[lim1_min,lim1_max];
L(2).qlim=[lim2_min,lim2_max];
L(3).qlim=[lim3_min,lim3_max];
L(4).qlim=[lim4_min,lim4_max];
L(5).qlim=[lim5_min,lim5_max];
L(6).qlim=[lim6_min,lim6_max];
robot = SerialLink(L,'name','AR3');
第三步,定义轨迹的起始点、中间点、终止点以及轨迹点个数
p_start = [200, 60,320]; %圆弧轨迹起始点
p_mid = [200, 60,400]; %圆弧轨迹中间点
p_final = [230,200,510]; %圆弧轨迹终止点
step = 50; %步数第四步,求取圆弧所在轨迹圆的半径
a = norm(p_final - p_mid); %内接三角形边长a
b = norm(p_final - p_start); %内接三角形边长b
c = norm(p_mid - p_start); %内接三角形边长c
l = (a + b + c) / 2; %内接三角形半周长
r = a*b*c/ 4 / sqrt(l*(l - a)*(l - b)*(l - c)); %轨迹圆半径第五步,求取圆弧所在平面方程的参数
solution = [p_start(1) p_start(2) p_start(3) ; p_mid(1) p_mid(2) p_mid(3) ; p_final(1) p_final(2) p_final(3) ] \ [1;1;1];
%A是一个方阵,A\B与inv(A)* B大致相同
第六步,求取圆弧所在轨迹圆圆心
%求取圆弧所在轨迹圆圆心
b1 = a*a * (b*b + c*c - a*a);
b2 = b*b * (a*a + c*c - b*b);
b3 = c*c * (a*a + b*b - c*c);
P1 = [p_start' p_mid' p_final'];
P2 = [b1; b2; b3];
P3 = P1 * P2;
center = P3 ./ (b1 + b2 + b3);
center = center';%转置第七步,求取末端执行器在圆弧上运动的旋转轴,过圆心且垂直圆所在平面
vector_start_big = p_start - center; %由圆心指向起点的向量
vector_start = (p_start - center) ./ norm(p_start - center); %由圆心指向起点的单位向量
vector_final = (p_final - center) ./ norm(p_start - center); %由圆心指向终点的单位向量
rotation_axis = cross(vector_start,vector_final); %旋转轴第八步,求取圆弧角度及每个轨迹点之间的角度
theta = acos(dot(vector_start , vector_final));%弧度制的圆弧角度
%theta = rad2deg(theta);%角度制的圆弧角度
theta_per = theta / step;%角度制的每个轨迹点之间的角度第九步,初始化轨迹点数组
theta_current = 0; %初始化当前路径点与起始点之间的角度
p_current = 0; %初始化轨迹点位置第十步,轨迹规划,生成轨迹点
for t = 1 : step + 1
matrix_current = rotation_matrix(rotation_axis,theta_current); %旋转矩阵的计算
vector_current = matrix_current * (vector_start_big'); %使向量绕旋转轴旋转
p_current = center + vector_current'; %轨迹点坐标
T_current=transl(p_current); %起始点齐次变换矩阵
Tc(:,:,t) = T_current; %保存轨迹点为齐次变化矩阵
theta_current = t * theta_per; %角度变化
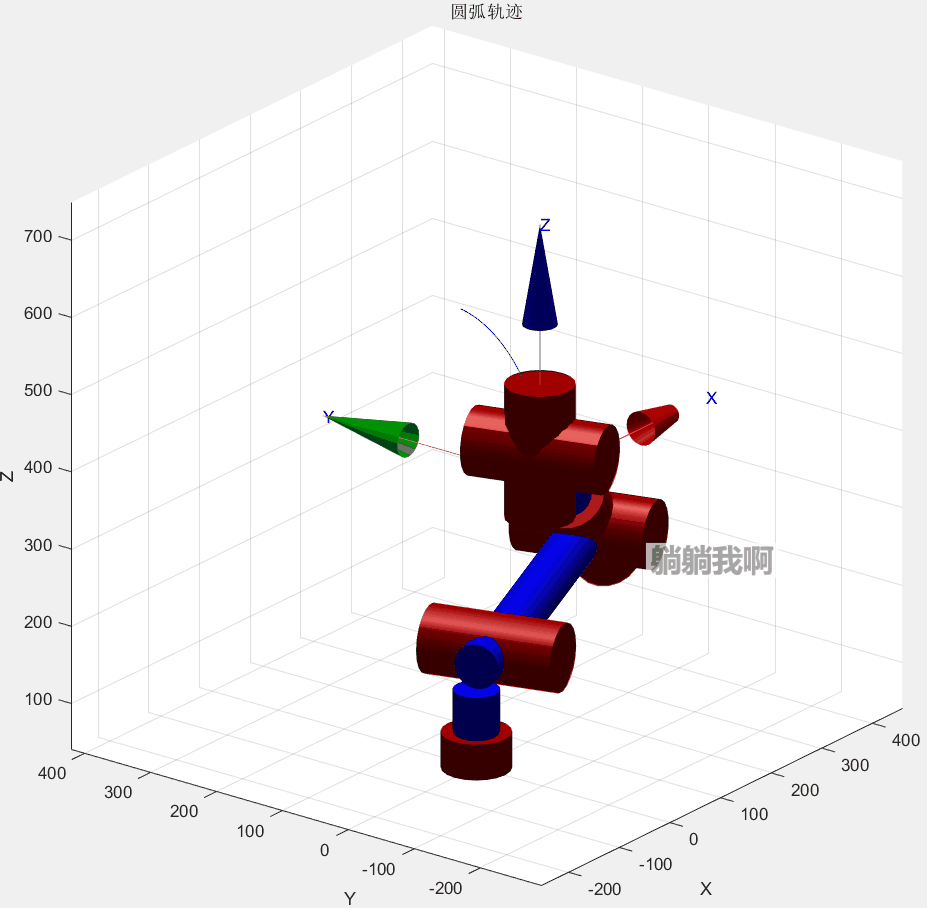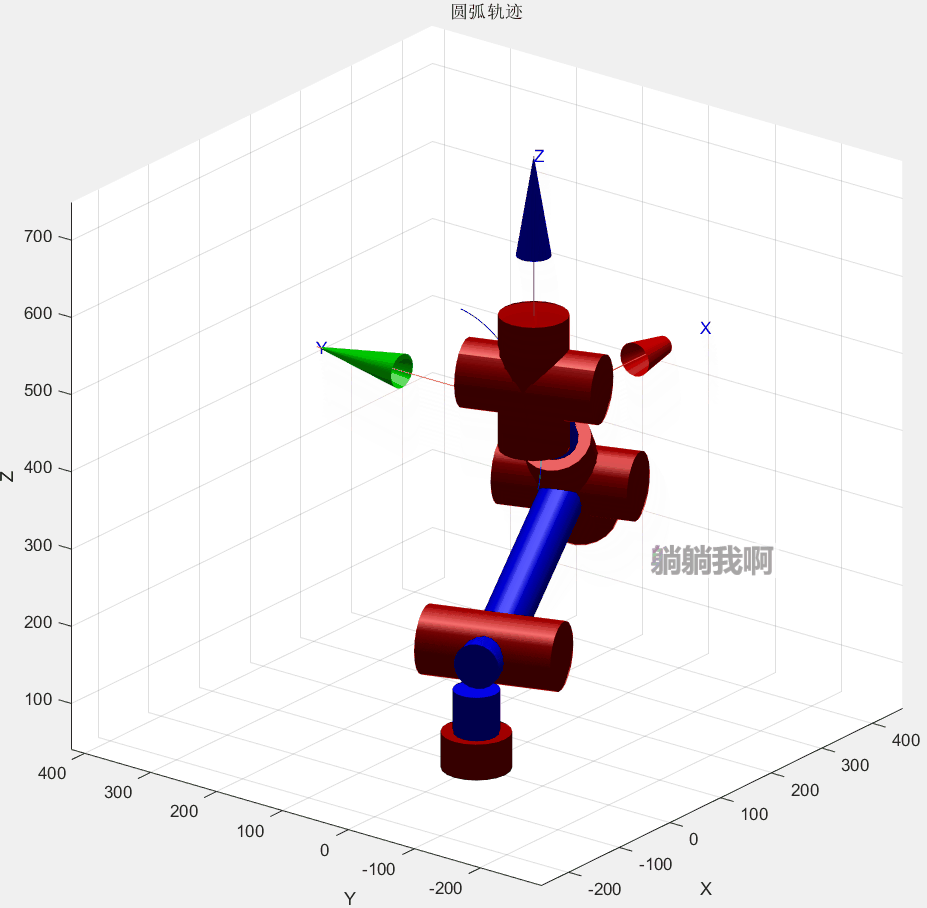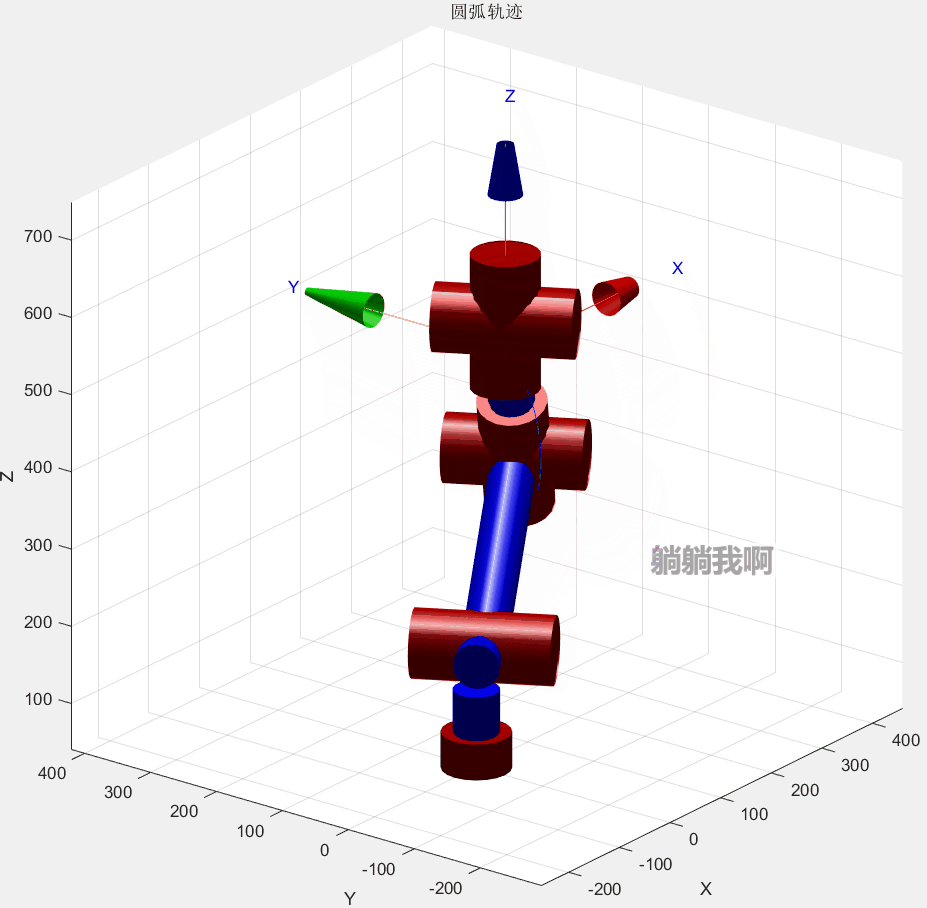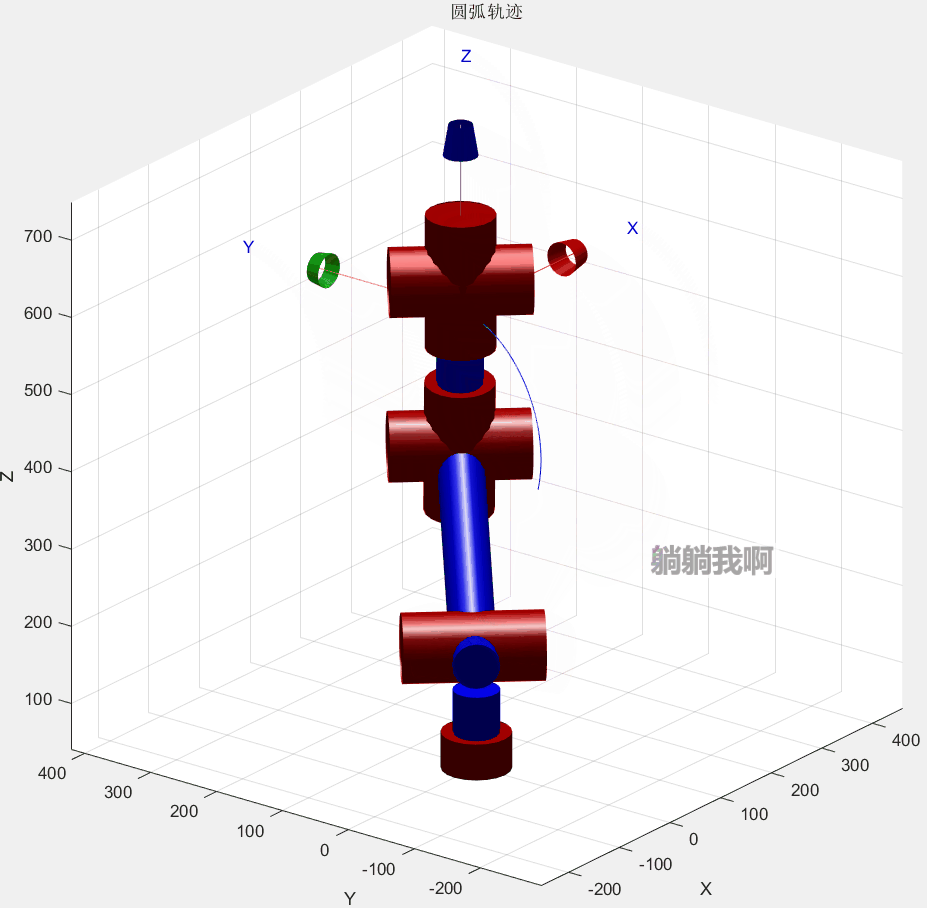
end最终效果如下所示
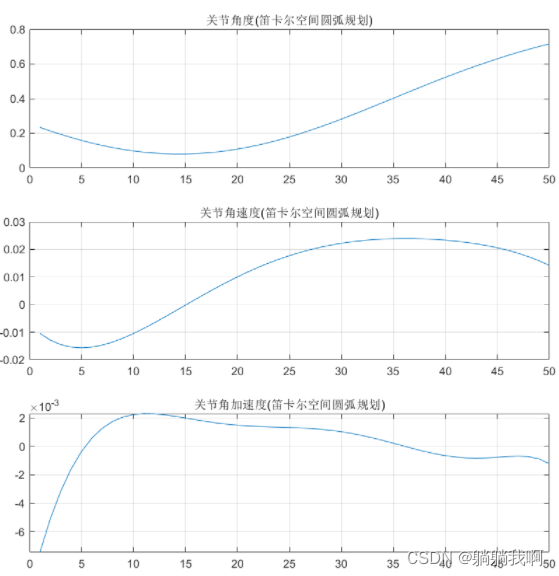
三、编程实现

其中红色圆弧为机械臂运动所得轨迹,蓝色虚线代表轨迹所在的轨迹圆,蓝点为其圆心。
需要资源的同学,可在评论区中留言。
边栏推荐
猜你喜欢
随机推荐
管理软件开发 管理软件定制开发流程
form的编辑与展示的切换(输入框,单选多选框,上传图片,颜色选择器)适用个人信息的展示与修改
做好私域流量!全民拼购就可以了。
MySQL-1-环境部署
2022 VMware下载安装教程
SIGIR'22 推荐系统论文之POI篇
入门关于 switch case 的理解
数组的应用实例—三子棋
Azure Kinect(K4A)人体识别跟踪进阶
PAT serie a 1137 final grades
第十五天笔记
Linux系统中mysql数据库的基本管理
VPP snort插件
Go-5-简单介绍fmt库
Advanced usage of vim configuration
WWW'22 推荐系统论文之序列推荐篇
虚拟现实处理器(SXR2130P)ISO7640FMDW(数字隔离器)说明
快速搞懂Seata分布式事务AT、TCC、SAGA、XA模式选型
性能测试详解(理论篇)
Qt | 设置部件大小 sizeHint、minimumSizeHint、sizePolicy、stretch factor