当前位置:网站首页>【论文精读】ROC和PR曲线的关系(The relationship between Precision-Recall and ROC curves)
【论文精读】ROC和PR曲线的关系(The relationship between Precision-Recall and ROC curves)
2022-08-05 05:15:00 【takedachia】
近期复习机器学习的一些基本知识,专门精读了一篇关于讲 ROC曲线的PR曲线关系的文章。
文章的title为《The relationship between Precision-Recall and ROC curves》发表于2006年,作者是来自威斯康辛大学麦迪逊分校的Jesse Davis和Mark Goadrich。虽然文章发表很早,但是涉及机器学习基石的知识永不会过时。
下面分享一下我的阅读笔记和心得。
文章目录
1 映射的视角看 混淆矩阵 与 ROC和PR曲线
简述 混淆矩阵
我们在评估一个二分类的模型的性能时,会使用一些评估指标,来评估其在测试集上的表现。
首先想到的就是准确率Accuracy,就是分类正确的占总数的比例。如果我们还想了解更详细的信息,比如一个临床医学问题中,我们的筛查模型会对检测阳性率比较关注,不愿意放过任何阳性的病人,那么我们就会关注Recall(又称查全率、敏感性)。
我们知道Recall = TP / (TP + FN),TP为真阳性,FN为假阴性。
每一个二分类模型在给定测试集上的一次分类结果,都可以表示为一张2×2的表,称为混淆矩阵(Confusion Matrix),四个指标分别为:TP(真阳性)、FN(假阴性)、FP(假阳性)、TN(真阴性)。如下图。
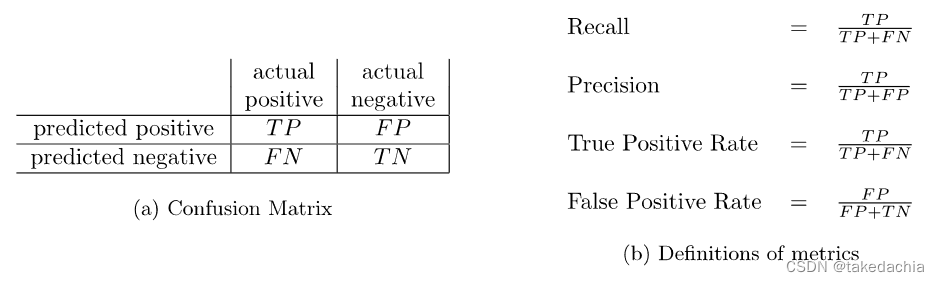
可以关注一下(a)混淆矩阵中各个指标的位置。图中第一列表示了真实阳性的预测情况,第二列表示了真实阴性的预测情况。
当然,在不同文献中,矩阵中actual和predict、positive和nagative常会位置互换,但是是一样的。
矩阵中这四个值常会用来表示 分类结果的评估指标,常见的如图(b),包括Recall(查全率、敏感性)、Precision(查准率)、True Positive Rate(真阳性率)、False Positive Rate(假阳性率)。
其中Recall=True Positive Rate。
ROC、PR曲线 是 混淆矩阵 到各自空间中映射的点集
我们知道一个二分类模型 在给定测试集上的一次分类结果可以给出一个 混淆矩阵。
而二分类模型的输出通常可以表示为正类的预测概率,比如输出 [0.28, 0.72],该向量表示第一类概率为0.3,第二类(设为正类)概率为0.7。我们默认把>0.5的概率表示为预测为当前类,这个0.5就是一个阈值(threshold)。
当阈值为0.5时,我们进行分类会得到一个分类结果,为一个混淆矩阵。当阈值为0.7时,我们又会得到一个混淆矩阵。当阈值为0.8时又会得到一个混淆矩阵(此时0.72<0.8,会被预测成负类)。
混淆矩阵不同,False Positive Rate、True Positive Rate、Recall、Precision会相应的变化。
我们把False Positive Rate、True Positive Rate这一对指标设为二维坐标系中的横纵坐标,就可以在这个坐标系中把不同的混淆矩阵对应的点标上去。无数的点就构成了ROC曲线。
如下图(a)。如果有两个不同的分类模型,就可以画出各自的ROC曲线。
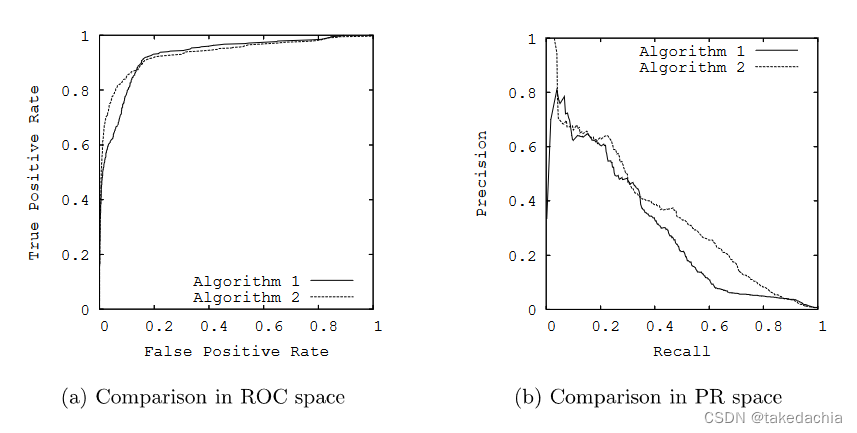
同理,我们把Recall、Precision这一对指标设为二维坐标系中的横纵坐标,同样可以在这个坐标系中把不同的混淆矩阵对应的点标上去。无数的这样的点就构成了PR曲线。如上图(b),不同的模型也会有不同的PR曲线。
这里,我自己将 混淆矩阵 和 两条曲线空间中的点 的对应法则比作函数,不同混淆矩阵分别映射ROC空间和PR空间中不同的点。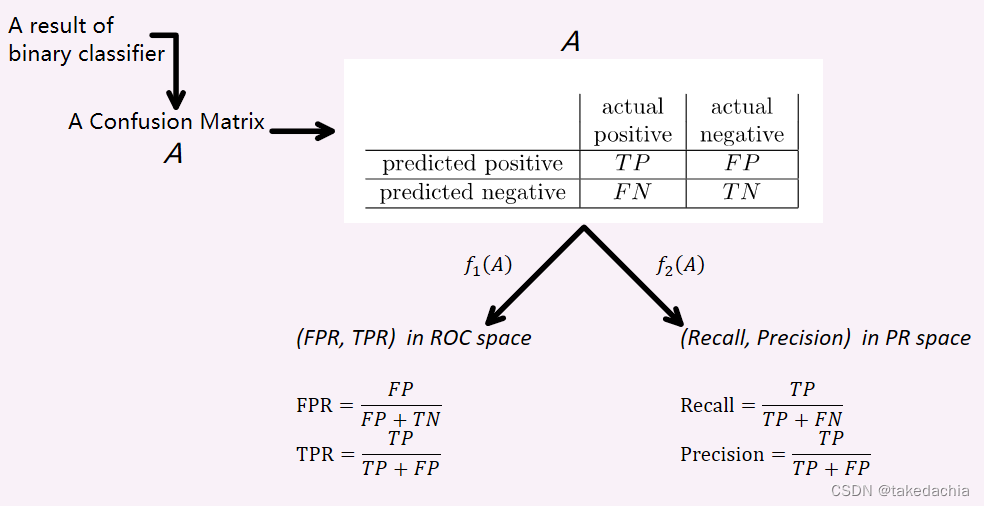
如图,一个二分类器的结果表示成混淆矩阵 A A A。
f 1 ( A ) f_1(A) f1(A)表示A映射到ROC空间中的一个点 ( F P R , T P R ) (FPR, TPR) (FPR,TPR)。
f 2 ( A ) f_2(A) f2(A)表示A映射PR空间中的一个点 ( R e c a l l , P r e c i s i o n ) (Recall, Precision) (Recall,Precision)。
A到空间中的点是一对一的映射,所有的点即组成了各自空间中的曲线,即ROC曲线和PR曲线。(这里的描述有助于理解论文中后面关于ROC曲线和PR曲线一一对应的证明)
同时,作者在文中提到还可以定义FPR、TPR、Recall、Precision为关于A的函数,譬如:
R E C A L L ( A ) = T P / ( T P + F N ) RECALL(A) = TP / (TP + FN) RECALL(A)=TP/(TP+FN)。
为什么PR曲线比ROC曲线更能反应不平衡类别样本的信息
我们先观察PR曲线和ROC曲线:
一个理想的二分类器,能把一个数据集完美的分类,它的混淆矩阵会是这样的(注意这是一个类别不平衡的数据集),仅正对角线上有值:
| Prediction Positive | Prediction Negative | |
|---|---|---|
| Actual Positive | 47 (TP) | 0 (FN) |
| Actual Negative | 0 (FP) | 433 (TN) |
ROC的横坐标FPR是第二行中FP比当前行,纵坐标TPR是第一行中TP比当前行。
PR的横坐标Recall是TP比这一行,纵坐标Precision是TP比这一列。
那么ROC曲线会无限拉到左上角,PR曲线会无限拉到右上角。
但是,现实中这是不太可能的,一般的混淆矩阵会是这样:
| Prediction Positive | Prediction Negative | |
|---|---|---|
| Actual Positive | 46 (TP) | 1 (FN) |
| Actual Negative | 33 (FP) | 400 (TN) |
在这个混淆矩阵里,我们看到假阳性FP相较于假阴性FN比较多(比如癌症筛查的模型,我们希望先查到更多阳性的,误抓了一些阴性的也不要紧)。
在ROC中,FPR和TPR依然都接近于1,点依然接近左上角。
但是在PR曲线中,Recall还是很漂亮,但是Precision=46/79,就降低了很多,点跑到了下方的位置: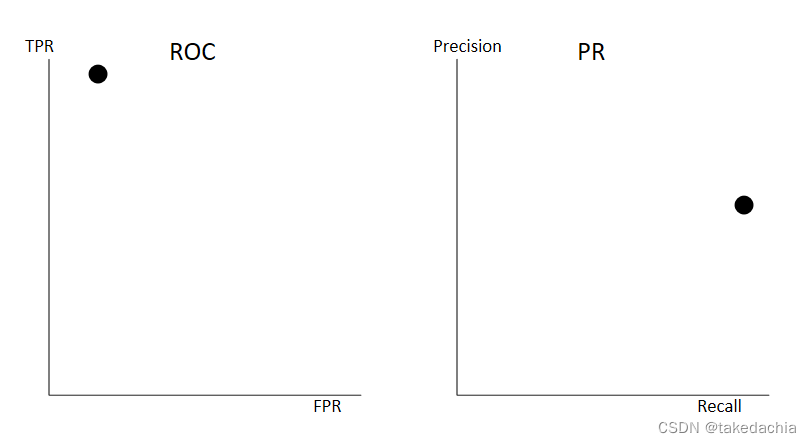
我们知道这是一个类别不平衡数据(Imbalanced Data),对于少数类,本身FP(或FN)的增加就会造成Precision(或Recall)的急剧下降。
对于PR曲线来说,横纵坐标Recall和Precision本身都关注了正类(少数类)的分类性能,关注点都聚焦在了某一个类上。(也可以关注多数类,把多数类设为正类,画出PR曲线,但是意义不大)
而对于ROC曲线,横纵坐标FPR和TPR关注的是各自类别的分类效率,所以自然而然对类别不平衡数据不敏感了。但相对的,ROC能同时关注到两个类,体现了分类器的综合分类性能。
因此,在实际问题中,ROC曲线首先可以反应分类器的综合性能,而当我们需要关注某个类别的分类性能(因为类别不平衡,如癌症的筛查)时,需要用PR曲线来观察。
当然,对于二分类器的性能指标,还有诸如F1-score等也可以衡量类别不平衡数据的分类性能。
2 ROC曲线与PR曲线可等价变换,两条曲线的点一一对应
我们知道对于给定的数据集,ROC曲线和PR曲线能反映分类器的分类性能,并且两者的展现的性能信息各有侧重,PR曲线更能显示不平衡类别的分类性能。我们就会思考一个问题,这两条曲线似乎提供了不同的信息,ROC和PR是两回事吗?
答案是两条曲线是一一对应的,作者在文中给出了一个定理:
给定的二分类数据集,(如果 Recall ≠ 0)ROC空间中的曲线与 PR空间中的曲线 之间存在一一对应关系,使得曲线包含完全相同的混淆矩阵。
证明(这里我自己证明描述和作者稍有不同,本质是一样的):
我们回到前面那张图: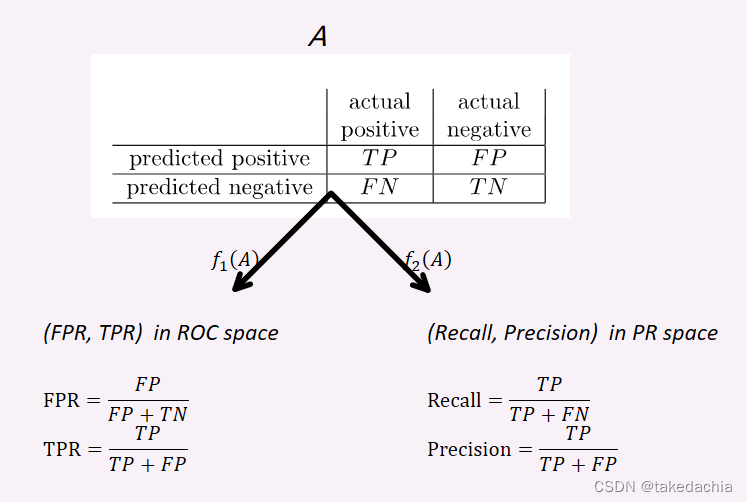
一个二分类器的结果表示成一个混淆矩阵 A A A,它有4个变量:TP、FP、FN、TN。由于数据集给定,四个变量的和即样本个数是确定的,因此矩阵的自由度是3。
f 1 ( A ) f_1(A) f1(A)表示A映射到ROC空间中的一个点 ( F P R , T P R ) (FPR, TPR) (FPR,TPR),观察图上的公式,可以看到坐标点只用到了3个变量:FP、TN、TP。第4个变量虽然没出现,但是唯一确定的, n − ( F P + T N + T P ) n-(FP+TN+TP) n−(FP+TN+TP)。因此 f 1 f_1 f1映射是一个一对一映射,在集合论中称为双射(单射+满射)。
f 2 ( A ) f_2(A) f2(A)同理,其表示A映射PR空间中的一个点 ( R e c a l l , P r e c i s i o n ) (Recall, Precision) (Recall,Precision),也是个自由度为3的输出。 f 2 f_2 f2映射也是一个一对一映射,为双射。
因为都是一对一映射,两个空间中的点都由唯一确定的混淆矩阵来表示,所以ROC空间和PR空间中的点一一对应,曲线包含完全相同的混淆矩阵。
最后,如果Recall=0即TP=0,将无法还原分母中FN、FP的值,无法逆解出混淆矩阵A的四个变量,因此Recall不能为0。
因此得证。
这个定理有什么作用呢?
我觉得第一,它告诉我们一个模型的ROC曲线和PR曲线包含完全相同的信息,只不过侧重展示了不同类别的分类性能,PR曲线不漂亮不意味着ROC曲线不行,它的综合分类性能(如准确率Accuracy)还是可以一看的。
第二,它为论文后面讨论的寻找最优ROC、PR曲线的可行性奠定理论基础。
3 ROC空间中,曲线A优于曲线B ⇔ PR空间中,曲线A优于曲线B
小标题中,曲线A优于曲线B,优于是什么意思呢?
在原文中使用了dominate的概念,曲线A统治曲线B,意为曲线A永远在曲线B的上方(允许局部贴合)。
在ROC空间中,曲线A dominate 曲线B,即意味着曲线A代表的分类器模型优于曲线B代表的。在PR空间中,也是一样的道理。我们可以简单的通过曲线下面积增减来理解这一现象。
证明,即证:
①在ROC空间,曲线A在曲线B之上 ⇨ 在PR空间,曲线B在曲线A之上
②在PR空间,曲线A在曲线B之上 ⇨ 在ROC空间,曲线B在曲线A之上
我们先证命题①,按照论文中作者的思想,我用反证法自己证明了一遍,证明过程如下:
命题②也可以用相同的思路用反证法得证。
我们看到证明过程用到了第2节中的定理,逻辑上承前启后。
那么这里又会有个疑问,为什么作者要提出占优(dominate)这个概念呢?是单纯的提升曲线下面积吗?
4 构建Convex Hull(凸包)绘制最大可实现ROC曲线
这里,作者在这篇文章中的研究很多是继承了另一篇文章《Realisable Classifiers: Improving Operating Performance on Variable Cost Problems.》(Scott,1998)的思想。在那篇文章中,作者提出了Convex Hull(凸包)的概念,通过对ROC空间中的已有点绘制凸包,可得到一条MRROC(最大可实现曲线)。
最大可实现曲线可理解为一种最优曲线(optimal curve),它可以给分类器算法的设计者们对更优建模的启示,提示我们当前的分类算法究竟是否合适。
在那篇文章的原文中,作者谈到:给定一个分类算法(如线性模型)和它生成一条ROC曲线,会有一个包络这条ROC曲线而构成的凸包。这个凸包代表了一系列可实现分类器,它们总是比这个线性模型要更优,并且它们是由初始分类器的子类创建的。给定一些已存在的分类器,构建的凸包就描述了一种最大可实现ROC。
凸包(Convex Hull)与最大可实现曲线
首先,什么是凸包 Convex Hull?
我们知道在平时,我们实际建模预测数据得到的ROC曲线是一般类似阶梯型的,如: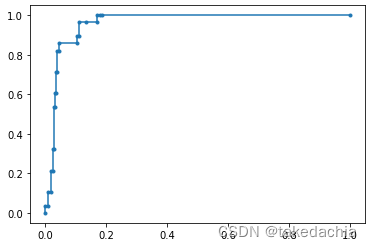
如果我们接触过凸优化理论,就知道这个曲线不“凸”,怎么构造“凸”呢?
摈弃文中的定义,我采用了网上大神的一张妙图,他把构建凸包比喻成拉一跟橡皮筋。
这跟红色的橡皮筋连接左下角和右上角的点,从左上角松开,凸包就是第3张图的状态,凸包就是这根橡皮筋上的点集。橡皮筋上所有的点都位于已有ROC点(线)的上方。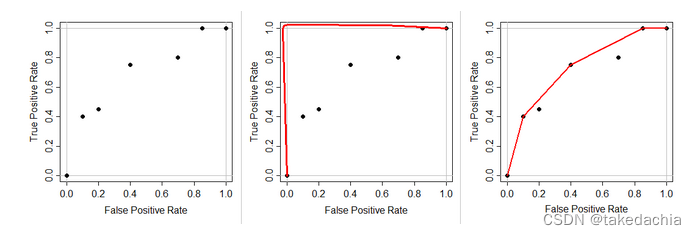
这也是文中dominate这一概念的由来,这个凸包就是一条最大可实现ROC曲线,它在这个ROC空间中占统治地位(dominate)。
《Realisable Classifiers: Improving Operating Performance on Variable Cost Problems.》一文的这张图片描述了多个分类器ROC曲线下,通过构建凸包绘制最大可实现ROC曲线 的实现: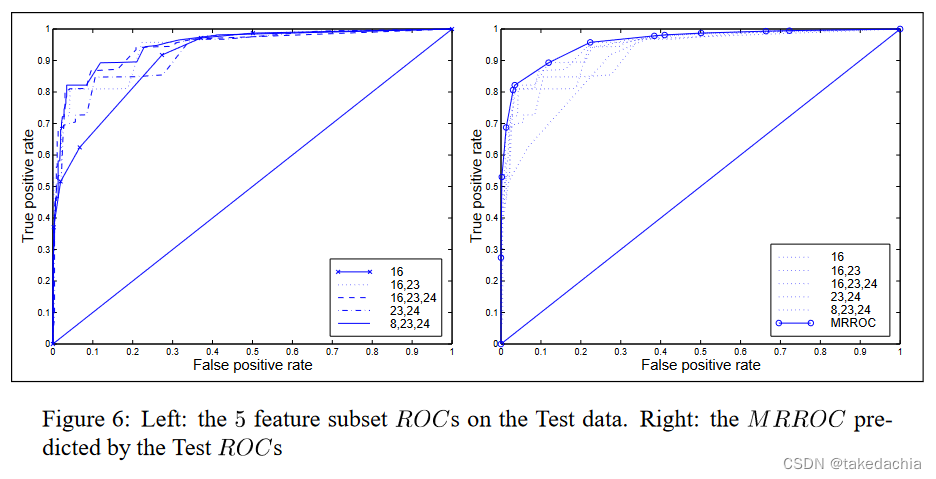
构建 可实现的PR曲线
基于我们通过构建凸包绘制最大可实现ROC曲线,作者在文中提出了一个推论:
在PR空间上也存在着 可实现的PR曲线(achievable P-R curve),它可以基于已有分类器的PR曲线构建,且achievable P-R curve在PR空间中占统治地位(dominate)。
证明方法使用了前面第2节的定理和第3节的结论,这里不详述。
可实现的PR曲线的构建不是简单的拉橡皮筋,可先在ROC空间中构建凸包,再将点转换过来。
文章的后半部分以比较大的篇幅讨论了 可实现的PR曲线 的构建方法,以及与曲线下面积的关系。
5 单纯优化ROC曲线下面积不能优化PR曲线下面积
我们知道了可通过构建 MRROC 和 achievable P-R curve 来构建最优曲线。
同时我们也知道ROC曲线下面积(AUC-ROC)在构建MRROC中会被优化(拉橡皮筋后,面积大了)。
那我们想,简单地通过算法优化 AUC-ROC,会相应地优化 PR曲线下面积吗?
答案是否定的,作者在文中举了一个比较极端的例子: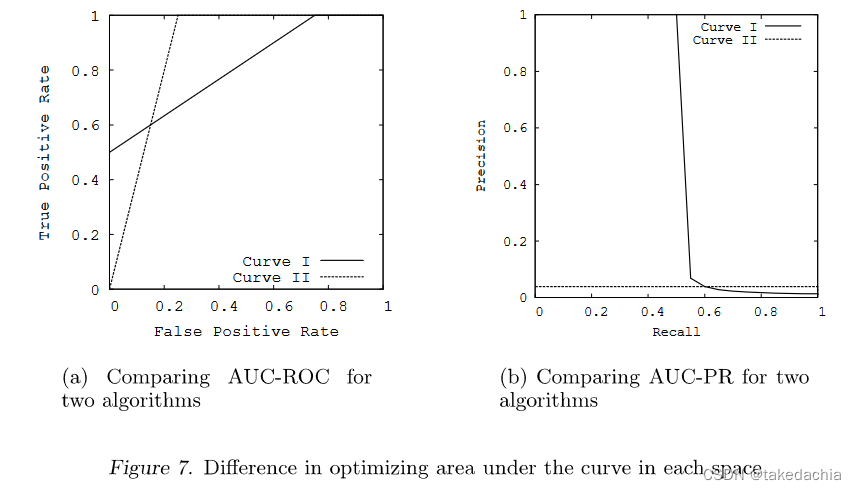
左图有两条ROC曲线,曲线Ⅰ的AUC=0.813,曲线Ⅱ的AUC=0.875,曲线Ⅰ面积<曲线Ⅱ面积。
但是对应到PR空间,曲线Ⅰ和曲线Ⅱ的样子变成了右图所示。曲线Ⅰ的PR曲线面积变得非常小。
从另一个角度也说明,在ROC空间中,曲线Ⅱ并没有统治曲线Ⅰ(相交),就只是面积大了点而已,不能说在PR空间中它们的大小就存在必然联系。
总结
- 对于任何一个数据集,一个分类器(模型)的ROC曲线和PR曲线包含了相同的点,它们之间是可以等价变换的。只是因为各自空间中横纵坐标的度量不同,各自展现了分类器的不同类别的分类性能。
- 由上可推出,当一条曲线在ROC空间中占统治地位(dominate)的时候,在PR空间中也占统治地位,反之亦然。
- 可以在ROC空间中构造一条最优曲线,方法是构建已有分类器点的凸包(Convex Hull),可理解为拉一条橡皮筋。将这个凸包的点转换到PR空间,可构成另一条最优曲线,称 可实现的PR曲线。
最优曲线可启发 算法设计者理解当前分类器的问题,设计更好的模型。 - 仅优化ROC曲线下面积不能保证优化PR曲线下面积。
参考文献:
《The relationship between Precision-Recall and ROC curves》Jesse Davis, Mark Goadrich. international conference on machine learning. Jun 2006
《Realisable Classifiers: Improving Operating Performance on Variable Cost Problems.》 Martin J.J.Scott, Mahesan Niranjan, Richard W. Prager. british machine vision conference. Jan 1998
边栏推荐
- Xiaobai, you big bulls are lightly abused
- flink项目开发-flink的scala shell命令行交互模式开发
- ES6 生成器
- 【NFT开发】设计师无技术基础保姆级开发NFT教程在Opensea上全套开发一个NFT项目+构建Web3网站
- 基于Flink CDC实现实时数据采集(四)-Sink接口实现
- 数据库期末考试,选择、判断、填空题汇总
- DOM及其应用
- 基于Flink CDC实现实时数据采集(三)-Function接口实现
- IDEA 配置连接数据库报错 Server returns invalid timezone. Need to set ‘serverTimezone‘ property.
- 怎么更改el-table-column的边框线
猜你喜欢
随机推荐
pycharm中调用Matlab配置:No module named ‘matlab.engine‘; ‘matlab‘ is not a package
Database experiment five backup and recovery
Matplotlib(一)—— 基础
Convert the paper official seal in the form of a photo into an electronic official seal (no need to download ps)
The software design experiment four bridge model experiment
学习总结week2_1
IDEA 配置连接数据库报错 Server returns invalid timezone. Need to set ‘serverTimezone‘ property.
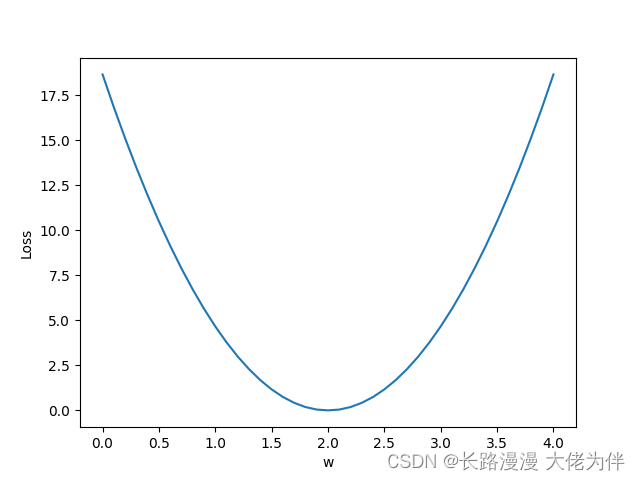
第5讲 使用pytorch实现线性回归
flink项目开发-flink的scala shell命令行交互模式开发
flink实例开发-详细使用指南
npm搭建本地服务器,直接运行build后的目录
Lecture 5 Using pytorch to implement linear regression
SQL(二) —— join窗口函数视图
有用番茄来监督自己的同道中人吗?加一下我的自习室,一起加油
基于Flink CDC实现实时数据采集(三)-Function接口实现
[Go through 11] Random Forest and Feature Engineering
如何编写一个优雅的Shell脚本(一)
轻松接入Azure AD+Oauth2 实现 SSO
Calling Matlab configuration in pycharm: No module named 'matlab.engine'; 'matlab' is not a package
What are the characteristics of the interface of the physical layer?What does each contain?