当前位置:网站首页>A detailed explanation takes you to reproduce the statistical learning method again -- Chapter 2, perceptron model
A detailed explanation takes you to reproduce the statistical learning method again -- Chapter 2, perceptron model
2022-07-02 09:11:00 【Qigui】
Individuality signature : The most important part of the whole building is the foundation , The foundation is unstable , The earth trembled and the mountains swayed .
And to learn technology, we should lay a solid foundation , Pay attention to me , Take you to firm the foundation of the neighborhood of each plate .
Blog home page : Qigui's blog
special column :《 Statistical learning method 》 The second edition —— Personal notes
It's not easy to create , Don't forget to hit three in a row when you pass by !!!
Focus on the author , Not only lucky , The future is more promising !!!Triple attack( Three strikes in a row ):Comment,Like and Collect--->Attention
One 、 Perceptron model
The perceptron is based on the feature vector of the input instance x A linear classification model for its second class classification , It's a discriminant model .
The hypothesis space of the perceptron model is all linear classification models or linear classifiers defined in the feature space ,
The set of functions  .
.
General form of perceptron model :
among ,x Represent eigenvectors ![[x_{1},x_{2},...,x_{i}].T](http://img.inotgo.com/imagesLocal/202207/02/202207020624132497_15.gif) ,
, and b It's a perceptron model parameter ,
and b It's a perceptron model parameter , It's called weight or weight vector
It's called weight or weight vector ![[\omega _{1},\omega _{2},...,\omega _{i}].T](http://img.inotgo.com/imagesLocal/202207/02/202207020624132497_8.gif) ,b Called bias (bias),
,b Called bias (bias), Express
Express  and x Inner product ,sign It's a symbolic function , namely
and x Inner product ,sign It's a symbolic function , namely 
The perceptron model corresponds to the separation hyperplane in the feature space :
The perceptron corresponds to a separating hyperplane that divides instances into positive and negative categories in the feature space S, among  Is the normal vector of the hyperplane ,b Is the intercept of the hyperplane . This hyperplane divides the feature space into two parts , The point in both parts ( Eigenvector ) They are called positive and negative respectively , The input is the eigenvector of the instance , The output is the category of the instance , take +1 and -1. So this hyperplane S It is called a separated hyperplane .
Is the normal vector of the hyperplane ,b Is the intercept of the hyperplane . This hyperplane divides the feature space into two parts , The point in both parts ( Eigenvector ) They are called positive and negative respectively , The input is the eigenvector of the instance , The output is the category of the instance , take +1 and -1. So this hyperplane S It is called a separated hyperplane .
The perceptron uses a hyperplane to divide instances into positive and negative classes , But some data sets are not linearly separable , So no hyperplane can correctly classify all instances .
in general , The instance points are classified by training the perceptron model , For example, red beans and mung beans are classified after mixing , At that time, a hyperplane is needed to divide the two classes and mark them as +1 and -1.
import numpy as np
def perceptron(x1, x2):
x = np.array([x1, x2]) # Eigenvector
w = np.array([0.3, 0.7]) # A weight
b = -0.3 # bias
f = np.sum(w * x) + b # General form of perceptron model
# f = np.dot(w, x) + b
# Divide the examples through model training
if f >= 0:
return 1 # Just like
else:
return -1 # Negative class
# Input eigenvector x
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = perceptron(x[0], x[1])
print(str(x) + '-->' + str(y))(0, 0)-->-1
(1, 0)-->1
(0, 1)-->1
(1, 1)-->1Two 、 Perceptron learning strategies
1、 Linear separability of data sets
If I have some hyperplane S The positive instance points and negative instance points of the data set can be completely and correctly divided into two sides of the hyperplane , For all  Example i, Yes
Example i, Yes  , For all
, For all  Example , Yes
Example , Yes  , Then the data set is called linear separable data set ; otherwise , Call the data set linearly indivisible . In reality , This data set is ideal , The existence may be small .
, Then the data set is called linear separable data set ; otherwise , Call the data set linearly indivisible . In reality , This data set is ideal , The existence may be small .
2、 Perceptron learning strategies
To find such a hyperplane , That is to determine the parameters of the perceptron model  ,b, Need to identify a learning strategy , This learning strategy is to define the loss function and minimize the loss function . Perceptron generally adopts : A natural choice of the loss function is the total number of misclassification points , Another choice of loss function is misclassification point
,b, Need to identify a learning strategy , This learning strategy is to define the loss function and minimize the loss function . Perceptron generally adopts : A natural choice of the loss function is the total number of misclassification points , Another choice of loss function is misclassification point  To the hyperplane S The total distance . The former loss function is not a parameter
To the hyperplane S The total distance . The former loss function is not a parameter  ,b Continuous differentiable function of , Difficult to optimize . such , Hypothetical hyperplane S The set of misclassification points is M, Then we can get all misclassification points to the hyperplane S The total distance , Thus the loss function of perceptron learning is obtained . Given the training data set , Loss function
,b Continuous differentiable function of , Difficult to optimize . such , Hypothetical hyperplane S The set of misclassification points is M, Then we can get all misclassification points to the hyperplane S The total distance , Thus the loss function of perceptron learning is obtained . Given the training data set , Loss function  yes
yes  ,b Continuous differentiable function of .
,b Continuous differentiable function of .
Minimize the loss function :
among ,M Set of misclassification points , This loss function is actually the empirical risk function of perceptron learning . The strategy of perceptron learning is to select the model parameters that minimize the loss function in the hypothesis space  ,b Is the perceptron model , Corresponding to the total distance from the misclassification point to the separation hyperplane .
,b Is the perceptron model , Corresponding to the total distance from the misclassification point to the separation hyperplane .
The loss function is nonnegative . If there is no misclassification point , The value of the loss function is 0. The fewer misclassification points , The closer the misclassification point is to the hyperplane , The smaller the value of the loss function . The loss function of a particular sample point : In case of misclassification, it is a parameter  ,b The linear function of , In the correct classification is 0.
,b The linear function of , In the correct classification is 0.
The learning strategy of perceptron is to minimize the loss function . To be able to classify correctly , We need to find a separation hyperplane to divide the instance points completely and correctly , To find the hyperplane, we need to solve the separated hyperplane, that is  Medium Parameters
Medium Parameters  ,b;x Is the input eigenvector . However, there are certain errors due to the fact that the classification cannot be guaranteed to be completely correct , At this time, we need a learning strategy, that is, the loss function , Minimize the error , Is to minimize the loss function .
,b;x Is the input eigenvector . However, there are certain errors due to the fact that the classification cannot be guaranteed to be completely correct , At this time, we need a learning strategy, that is, the loss function , Minimize the error , Is to minimize the loss function .
3、 ... and 、 Perceptron learning algorithm
Learn the appropriate value within the value range , The output of the model calculated for the given input eigenvector is the predicted value , Be as correct as possible , Such algorithm is the learning algorithm of perceptron model .
Perceptron is an error driven learning algorithm . If the prediction is correct , The perceptron algorithm will continue to predict the next instance ; If the prediction is wrong , The algorithm will update the weights , to  updated .
updated .
1、 The original form of perceptron learning algorithm
The perceptron learning algorithm is misclassified driven , The random gradient descent method is used . First, select a hyperplane arbitrarily  , Then the gradient descent method is used to continuously minimize the loss function, resulting in the minimum value . The minimization process does not make M The gradient of all misclassification points in , Instead, one misclassification point is randomly selected at a time to make its gradient drop .
, Then the gradient descent method is used to continuously minimize the loss function, resulting in the minimum value . The minimization process does not make M The gradient of all misclassification points in , Instead, one misclassification point is randomly selected at a time to make its gradient drop .
Randomly select a classification error point  , Yes
, Yes  updated :
updated :
# Initialize parameters w, b
w = np.array([0.3, 0.7]) # A weight w
b = -0.3 # bias b
# Set the learning rate η
learning_rate = 0.6
# Yes w,b updated
def update_weights(x, y, w, b):
w = w + learning_rate * y * x
b = b + learning_rate * y
return w, b among  It's the step length , Also known as learning rate . Usually , The learning algorithm adjusts the range of updating parameters by setting the learning rate . Through iteration, we can expect the loss function to decrease , Until 0.
It's the step length , Also known as learning rate . Usually , The learning algorithm adjusts the range of updating parameters by setting the learning rate . Through iteration, we can expect the loss function to decrease , Until 0.
explain : When an instance point is misclassified , That is, on the wrong side of the separation hyperplane , Then adjust  Value , Move the separation hyperplane to one side of the misclassification point , To reduce the distance between the misclassification point and the hyperplane , Until the hyperplane crosses the misclassification point to make it classify correctly .
Value , Move the separation hyperplane to one side of the misclassification point , To reduce the distance between the misclassification point and the hyperplane , Until the hyperplane crosses the misclassification point to make it classify correctly .
To minimize the loss function , The method used is the gradient descent method . Gradient descent is to update the misclassification points , So as to change the parameters  ,b Value , Find the separation hyperplane . During the update process , in order to Limit
,b Value , Find the separation hyperplane . During the update process , in order to Limit  ,b The magnitude of change in the value of , Set a learning rate to adjust the magnitude .
,b The magnitude of change in the value of , Set a learning rate to adjust the magnitude .
2、 The convergence of the algorithm
Every time we traverse all the training instances, we call it a training cycle (epoch). If the learning algorithm classifies all training instances correctly in a training cycle , Then it reaches the convergence state .( Learning algorithms do not necessarily guarantee convergence , Therefore, the learning algorithm needs a super parameter to specify the maximum trainable cycle that can be completed before the algorithm terminates .)
After a finite number of iterations, we can get a separate hyperplane and perceptron model that completely and correctly divides the training data set , When the training data set is linearly separable , The original form iteration of perceptron learning algorithm is convergent ; Then when the training data set is linearly nonseparable , Perceptron learning algorithm does not converge , The iteration result will fluctuate . However, due to different initial values or different misclassification points , The solution can be different ; That is to say, there are many solutions to the perceptron learning algorithm , These solutions depend on the choice of initial values , It also depends on the selection order of misclassification points in the iterative process . To get the only hyperplane , We need to add constraints to the separation hyperplane .
3、 Dual form of perceptron learning algorithm
The basic idea : take  Represented as an instance
Represented as an instance  And tags
And tags  Of linear combinations of , By solving its coefficient
Of linear combinations of , By solving its coefficient  . The more instance points are updated , It means that the closer it is to the separation hyperplane , The more difficult it is to classify correctly , Examples at this time have the greatest impact on school results . Same as the original form , The dual form iteration of perceptron learning algorithm is convergent , There are multiple solutions .
. The more instance points are updated , It means that the closer it is to the separation hyperplane , The more difficult it is to classify correctly , Examples at this time have the greatest impact on school results . Same as the original form , The dual form iteration of perceptron learning algorithm is convergent , There are multiple solutions .
《 Statistical learning method 》—— The third chapter 、K Nearest neighbor method
http://t.csdn.cn/wBQab http://t.csdn.cn/wBQab
http://t.csdn.cn/wBQab
data structure 1800 test questions .pdf(C Language version ):
https://download.csdn.net/download/weixin_64215932/85253966 https://download.csdn.net/download/weixin_64215932/85253966
https://download.csdn.net/download/weixin_64215932/85253966
Reference material
1.《 Statistical learning method 》 The second edition -- expericnce
2.《scikit-learn machine learning 》 The second edition -- Gavin . Written by Haike , Translated by Zhang Haoran
3. Stanford machine learning PPT edition
边栏推荐
- C4D quick start tutorial - C4d mapping
- Use of libusb
- Pdf document of distributed service architecture: principle + Design + practice, (collect and see again)
- Cloudreve自建云盘实践,我说了没人能限制得了我的容量和速度
- 寻找链表中值域最小的节点并移到链表的最前面
- Matplotlib剑客行——初相识Matplotlib
- Solution and analysis of Hanoi Tower problem
- cmd窗口中中文呈现乱码解决方法
- Servlet全解:继承关系、生命周期、容器和请求转发与重定向等
- Cartoon rendering - average normal stroke
猜你喜欢

西瓜书--第六章.支持向量机(SVM)
ORA-12514问题解决方法

我服了,MySQL表500W行,居然有人不做分区?

Talk about the secret of high performance of message queue -- zero copy technology

队列管理器running状态下无法查看通道
Solution of Xiaomi TV's inability to access computer shared files
MYSQL安装出现问题(The service already exists)
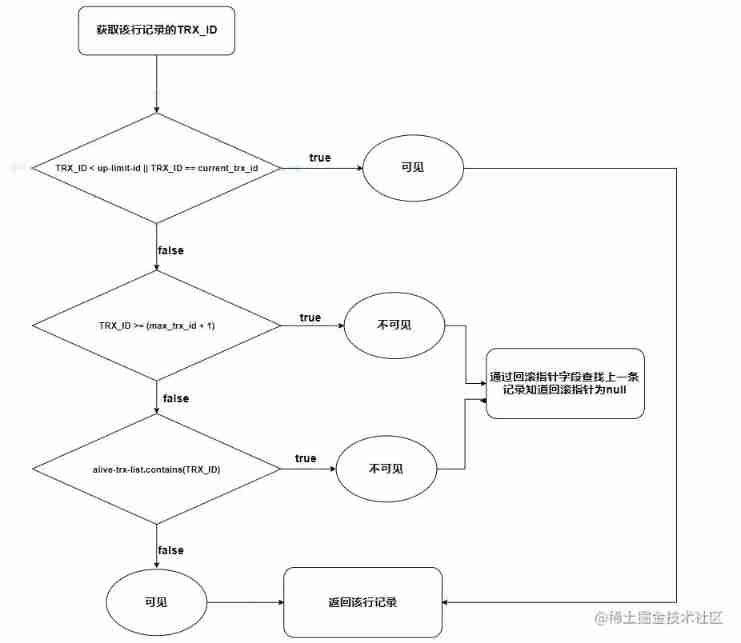
Multi version concurrency control mvcc of MySQL
「Redis源码系列」关于源码阅读的学习与思考

WSL安装、美化、网络代理和远程开发
随机推荐
C4D quick start tutorial - C4d mapping
Matplotlib剑客行——布局指南与多图实现(更新)
Oracle delete tablespace and user
Right click menu of QT
Win10 uses docker to pull the redis image and reports an error read only file system: unknown
Cartoon rendering - average normal stroke
win10使用docker拉取redis镜像报错read-only file system: unknown
[go practical basis] how to set the route in gin
Flink - use the streaming batch API to count the number of words
【Go实战基础】如何安装和使用 gin
微服务实战|手把手教你开发负载均衡组件
Count the number of various characters in the string
聊聊消息队列高性能的秘密——零拷贝技术
Leetcode sword finger offer brush questions - day 22
Programmers with ten years of development experience tell you, what core competitiveness do you lack?
Finishing the interview essentials of secsha system!!!
Move a string of numbers backward in sequence
微服务实战|负载均衡组件及源码分析
ORA-12514问题解决方法
Gocv image reading and display