当前位置:网站首页>Dynamic programming (tree DP)
Dynamic programming (tree DP)
2022-07-06 04:27:00 【D αī s ч】
( One )、 Basics
Tree form d p dp dp It's in the tree d f s dfs dfs In the middle of d p dp dp, In tree form d p dp dp in , Our dynamic planning process is probably to recursively access all subtrees first , Then merge on the root , We often solve all the optimal solutions in the range of subtrees
( Two )、 Example
1、 The size of the subtree
(1)、 The question : Calculate the size of the subtree of each point
(2)、 Answer key :
State means : s z [ u ] sz[u] sz[u] representative u u u Is the size of the root's subtree
State shift : s z [ u ] = 1 + ∑ s z [ v ] sz[u]=1+\sum sz[v] sz[u]=1+∑sz[v], It means that the size of the subtree of this node is equal to the sum of the sizes of all subtrees of the child node plus one
int sz[maxn];
void dfs(int u, int fa)
{
sz[u] = 1;
for (int i = head[u]; i; i = nex[i])
{
int v = to[i];
if (v != fa)
{
dfs(v, u);
sz[u] += sz[v];
}
}
}
2、 The balance point of the tree
(1)、 The question : Here you are n n n A dot tree , Find the balance point of the tree and the maximum number of nodes of the subtree after deleting the balance point . Balance point , It refers to a point in the tree , After deleting this point, the number of block nodes of the largest connected block among the remaining connected blocks is minimized
(2)、 Answer key :
State means : d p [ u ] dp[u] dp[u] It means deleting nodes i i i The size of the last block
State shift : d p [ u ] = m a x ( n − s z [ u ] , m a x ( s z [ v ] ) ) dp[u]=max(n-sz[u],max(sz[v])) dp[u]=max(n−sz[u],max(sz[v])), delete u u u The largest block after the node is either to remove the subtree u u u The rest of the connected blocks , Or nodes u u u The subtree of , The biggest one is d p [ u ] dp[u] dp[u]
int sz[maxn], dp[maxn];
int ans, idx, n;
void dfs(int u, int fa)
{
sz[u] = 1;
int maxx = 0;
for (int i = head[u]; i; i = nex[i])
{
int v = to[i];
if (v != fa)
{
dfs(v, u);
sz[u] += sz[v];
maxx = max(maxx, sz[v]);
}
}
maxx = max(maxx, n - sz[u]);
if (ans > maxx)
{
idx = u;
ans = maxx;
}
}
3、 The largest independent set
(1)、 The question : Yes n n n Staff , The number is 1 − n 1-n 1−n, Their relationship is like a tree rooted in the boss , The parent node is the direct superior of the child node . Every employee has a happiness index , Integers a i a_i ai give , Now there is going to be an anniversary party , Ensure that employees and their superiors do not attend the meeting at the same time , Make the total happiness index of all participants the largest , Find this maximum
(2)、 Answer key :
State means : d p [ u ] [ 0 ] dp[u][0] dp[u][0] It means the first one u u u The maximum value when employees do not participate , d p [ u ] [ 1 ] dp[u][1] dp[u][1] Express u u u The maximum number of employees participating
State shift :
d p [ u ] [ 0 ] = ∑ m a x ( d p [ v ] [ 1 ] , d p [ v ] [ 0 ] ) dp[u][0]=\sum max(dp[v][1],dp[v][0]) dp[u][0]=∑max(dp[v][1],dp[v][0]) If u u u Don't go to the dance , Then the child node v v v You may or may not participate
d p [ u ] [ 1 ] = a [ i ] + ∑ d p [ u ] [ 0 ] dp[u][1]=a[i]+\sum dp[u][0] dp[u][1]=a[i]+∑dp[u][0] If u u u Go to the ball , Then the child node v v v Do not participate , And node u u u Add your own happiness value
vector<int>g[maxn];
int dp[maxn][3];
int a[maxn];
void dfs(int u)
{
dp[u][0] = 0;
dp[u][1] = a[u];
for (int i = 0; i < g[u].size(); i++)
{
int v = g[u][i];
dfs(v);
dp[u][0] += max(dp[v][0], dp[v][1]);
dp[u][1] += dp[v][0];
}
}
ans = max(dp[root][0], dp[root][1]);
4、 Minimum point coverage
(1)、 The question : Here you are n n n A dot tree , There is at most one edge between every two points . If you put a soldier on a node , Then he can guard the side connected with it , Ask how many soldiers at least , To put all edge Can see hold
(2)、 Answer key :
State means :
d p [ u ] [ 0 ] dp[u][0] dp[u][0] It means that the soldiers are not released and u u u The minimum number of soldiers seen on each side of a rooted subtree
d p [ u ] [ 1 ] dp[u][1] dp[u][1] It means releasing soldiers and u u u The minimum number of soldiers seen on each side of a rooted subtree
State shift :
u u u Don't let go of the soldiers : d p [ u ] [ 0 ] = ∑ d p [ v ] [ 1 ] dp[u][0]=\sum dp[v][1] dp[u][0]=∑dp[v][1]
u u u Let the soldiers go : d p [ u ] [ 1 ] = 1 + ∑ m i n ( d p [ v ] [ 1 ] , d p [ v ] [ 0 ] ) dp[u][1]=1+\sum min(dp[v][1],dp[v][0]) dp[u][1]=1+∑min(dp[v][1],dp[v][0])
vector<int>g[maxn];
int dp[maxn][3];
void dfs(int u)
{
dp[u][1] = 1, dp[u][0] = 0;
for (int i = 0; i < g[u].size(); i++)
{
int v = g[u][i];
dfs(v);
dp[u][1] += min(dp[v][0], dp[v][1]);
dp[u][0] += dp[v][1];
}
}
5、 The minimum dominating set
(1)、 The question : Here you are n n n A dot tree , There is at most one edge between every two points . If in the first place i i i Deploy a signal tower at one point , You can make it and all the points connected to it receive signals . Ask how many signal towers can be deployed at least to make all spot Can receive signals
(2)、 Answer key : Pay attention to whether the choice of a point will affect not only the son but also the father's choice
State means :
d p [ u ] [ 0 ] dp[u][0] dp[u][0] Choose a point u u u, And in u u u The minimum number of signal tower deployments covered by each point of the root subtree
d p [ u ] [ 1 ] dp[u][1] dp[u][1] Indicates that no point is selected u u u, also u u u Minimum number of signal tower deployments covered by sons
d p [ u ] [ 2 ] dp[u][2] dp[u][2] Indicates that no point is selected u u u, however u u u Not covered by my son , And in u u u The minimum number of signal tower deployments that are covered by other points of the root subtree , That is to say, you need to choose u u u Father to cover u u u
State shift :
d p [ u ] [ 0 ] = 1 + ∑ m i n ( f [ v ] [ 0 ] , f [ v ] [ 1 ] , f [ v ] [ 2 ] ) dp[u][0]=1+\sum min(f[v][0],f[v][1],f[v][2]) dp[u][0]=1+∑min(f[v][0],f[v][1],f[v][2]), choice u u u After the point , The son node can be selected or not
d p [ u ] [ 2 ] = ∑ m i n ( f [ v ] [ 0 ] , f [ v ] [ 1 ] ) dp[u][2]=\sum min(f[v][0],f[v][1]) dp[u][2]=∑min(f[v][0],f[v][1]) When we don't choose u u u, also v v v When not covered , Its sons are at least covered or not chosen
When we don't choose u u u, also u u u When covered , And there are d p [ v ] [ 0 ] ≤ d p [ v ] [ 1 ] dp[v][0]\leq dp[v][1] dp[v][0]≤dp[v][1], This is our choice u u u It won't be worse , So we choose u u u, here d p [ u ] [ 1 ] = ∑ m i n ( f [ v ] [ 0 ] , f [ v ] [ 1 ] ) dp[u][1]=\sum min(f[v][0],f[v][1]) dp[u][1]=∑min(f[v][0],f[v][1]); If there is no such son , Then we need to choose one with the least loss , here d p [ u ] [ 1 ] = ∑ m i n ( f [ v ] [ 0 ] , f [ v ] [ 1 ] ) + m i n ( d p [ v ] [ 0 ] − d p [ v ] [ 1 ] ) dp[u][1]=\sum min(f[v][0],f[v][1])+min(dp[v][0]-dp[v][1]) dp[u][1]=∑min(f[v][0],f[v][1])+min(dp[v][0]−dp[v][1])
int dp[maxn][4];
void dfs(int u, int fa)
{
dp[u][0] = 1, dp[u][1] = dp[u][2] = 0;
int tmp = inf;
bool flag = 1;
for (int i = 0; i < g[u].size(); ++i)
{
int v = g[u][i];
if (v == fa)
continue;
dfs(v, u);
dp[u][2] += min(dp[v][1], dp[v][0]);
dp[u][0] += min(dp[v][0], min(dp[v][1], dp[v][2]));
if (dp[v][0] <= dp[v][1])
{
flag = 0;
dp[u][1] += dp[v][0];
}
else
{
dp[u][1] += dp[v][1];
tmp = min(tmp, dp[v][0] - dp[v][1]);
}
}
if (flag)
dp[u][1] += tmp;
}
Another way to do it :
int over[maxn], ans;
void dfs(int u, int fa)
{
bool flag = 0;
for (int i = 0; i < e[u].size(); i++)
{
int v = e[u][i];
if (v != fa)
{
dfs(v, u);
flag |= over[v];
}
}
if (!flag && !over[u] && !over[fa]) // If u In itself 、 son 、 The parent node has not been traversed
{
over[fa] = 1;
ans += 1;
}
}
6、 Tree backpack
(1)、 The question : Yes n n n Items and a load bearing are m m m The backpack . There is a dependency between objects , And dependencies make up the shape of a tree . If you choose an item , Then its parent section must be selected spot . solve m m m The maximum value that can be installed under load
(2)、 Answer key : First dimensional enumeration subtree , The second dimension enumerates the capacity , The third dimension enumerates decisions ( That is, how much weight is allocated to the subtree )
State means : d p [ u ] [ i ] dp[u][i] dp[u][i] On behalf of u u u Select items for the points of the subtree , The bearing capacity does not exceed i i i The greatest value you can get when you're in the market
State shift : d p [ u ] [ i ] = m a x ( d p [ u ] [ i ] , d p [ u ] [ i − j ] + d p [ v ] [ j ] ) dp[u][i]=max(dp[u][i],dp[u][i-j]+dp[v][j]) dp[u][i]=max(dp[u][i],dp[u][i−j]+dp[v][j])
vector<int>g[maxn];
int n, m;
int weight[maxn], val[maxn];
void dfs(int u)
{
for (int i = weight[u]; i <= m; i++)
dp[u][i] = val[u]; // Because only the root node is selected , Will continue to traverse down , Therefore, the root node is selected first
for (auto v : g[u])
{
dfs(v);
for (int i = m; i >= weight[u]; i--) // If the remaining weight is less than the total weight of the root node, it is impossible to take
{
for (int j = 0; j <= i - weight[u]; j++) // Give the weight of the subtree j The remaining after cannot be less than weight[u]
{
dp[u][i] = max(dp[u][i], dp[u][i - j] + dp[v][j]);
}
}
}
}
7、 A binary apple tree ( Tree backpack )
(1)、 The question : Given a tree n n n A dot binary tree , Each side has its own right a i a_i ai, Retain m m m The article edge , Make the edge weight and maximum of the reserved edge
(2)、 Answer key : This topic is similar to tree knapsack , But the difference is point and edge
State means : d p [ u ] [ i ] dp[u][i] dp[u][i] On behalf of u u u Select edges for the subtree , At capacity not exceeding i i i The greatest value you can get when you're in the market
State shift : d p [ u ] [ i ] = m a x ( d p [ u ] [ i ] , d p [ u ] [ i − j − 1 ] + d p [ v ] [ j ] + w [ i ] ) dp[u][i]=max(dp[u][i],dp[u][i-j-1]+dp[v][j]+w[i]) dp[u][i]=max(dp[u][i],dp[u][i−j−1]+dp[v][j]+w[i])
void dfs(int u)
{
for (auto node : g[u])
{
int v = node.first;
int w = node.second;
dfs(v);
for (int i = m; i >= 1; i--)
{
for (int j = 0; j <= i - 1; j++)
{
dp[u][i] = max(dp[u][i], dp[u][i - j - 1] + dp[v][j] + w);
}
}
}
}
8、 The diameter of the tree ( See graph theory for details )
9、 S T A − S t a t i o n STA-Station STA−Station
(1)、 The question : Given a n n n A dot tree , Request a node , Let this node be the root , The depth sum of all nodes is the largest
(2)、 Answer key : Tree form d p dp dp Change the root in d p dp dp The problem is also called secondary scanning , The root node is usually not specified , And the change of the root node will affect some values , For example, child node depth and 、 Point weight and have an impact . Usually twice d f s dfs dfs, for the first time d f s dfs dfs Deal with things like depth , Point weight and other information , In the second time d f s dfs dfs Start to change the root d p dp dp
For this problem, we can start from any point to find the a n s ans ans, Then change the root d p dp dp, Find the corresponding a n s ans ans
State means : d p [ u ] dp[u] dp[u] Said to u u u Root , Sum of all node depths
State shift : d p [ v ] = d p [ u ] − s z [ v ] + ( n − s z [ v ] ) dp[v]=dp[u]-sz[v]+(n-sz[v]) dp[v]=dp[u]−sz[v]+(n−sz[v])
ll dp[maxn];
vector<int>g[maxn];
int n;
ll deep[maxn], sz[maxn];
void dfs1(int u, int fa)
{
sz[u] = 1;
deep[u] = deep[fa] + 1;
for (auto v : g[u])
{
if (v != fa)
{
dfs1(v, u);
sz[u] += sz[v];
}
}
}
void dfs2(int u, int fa)
{
for (auto v : g[u])
{
if (v != fa)
{
dp[v] = dp[u] - sz[v] + (n - sz[v]);
dfs2(v, u);
}
}
}
void solve()
{
cin >> n;
for (int i = 1; i < n; i++)
{
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs1(1, 0);
for (int i = 1; i <= n; i++)
{
dp[1] += deep[i];
}
dfs2(1, 0);
int idx = 1;
for (int i = 1; i <= n; i++)
{
if (dp[idx] < dp[i])
idx = i;
}
cout << idx << '\n';
}
10、 Road reversal
(1)、 The question : A country has n n n Cities , This country has n − 1 n-1 n−1 A one-way passage connecting the two cities . Now we need to choose a capital , And this city can lead to any other city , But in order to meet this requirement , Some channels may need to be reversed . How to choose the capital , It can minimize the number of channels that need to be reversed
(2)、 Answer key : We can first find the path that needs to be reversed from any point : Build two-way side , There is no need to reverse the edge weight to 0, You need to reverse the edge weight to 1; Then we change the root d p dp dp Find out the a n s ans ans
State means : d p [ u ] dp[u] dp[u] Said to u u u The city as the capital needs to reverse the road
State shift :
If the road needs to be reversed , Then there is no need to reverse for the son node d p [ v ] = d p [ u ] − 1 dp[v]=dp[u]-1 dp[v]=dp[u]−1
If the road does not need to be reversed , For the son node, you need to reverse d p [ v ] = d p [ u ] + 1 dp[v]=dp[u]+1 dp[v]=dp[u]+1
int dp[maxn];
int to[maxn << 1], nex[maxn << 1], w[maxn << 1], head[maxn], cnt;
int cost[maxn];
void add(int u, int v, int we)
{
to[++cnt] = v;
w[cnt] = we;
nex[cnt] = head[u];
head[u] = cnt;
}
void dfs1(int u, int fa)
{
for (int i = head[u]; i; i = nex[i])
{
int v = to[i];
if (v != fa)
{
dfs1(v, u);
cost[u] += cost[v] + w[i];
}
}
}
void dfs2(int u, int fa)
{
for (int i = head[u]; i; i = nex[i])
{
int v = to[i];
if (v != fa)
{
if (w[i])
dp[v] = dp[u] - 1;
else
dp[v] = dp[u] + 1;
dfs2(v, u);
}
}
}
void solve()
{
int n;
cin >> n;
for (int i = 0; i < n - 1; i++)
{
int u, v;
cin >> u >> v;
add(u, v, 0);
add(v, u, 1);
}
dfs1(1, 0);
dp[1] = cost[1];
dfs2(1, 0);
int minv = inf;
for (int i = 1; i <= n; i++)
{
minv = min(minv, dp[i]);
}
cout << minv << '\n';
for (int i = 1; i <= n; i++)
{
if (dp[i] == minv)
{
cout << i << ' ';
}
}
}
边栏推荐
- Global and Chinese market of rubber wheel wedges 2022-2028: Research Report on technology, participants, trends, market size and share
- Can Flink SQL read multiple topics at the same time. How to write in with
- HotSpot VM
- Codeforces Round #770 (Div. 2) B. Fortune Telling
- CADD课程学习(8)-- 化合物库虚拟筛选(Virtual Screening)
- Sentinel sliding window traffic statistics
- About some basic DP -- those things about coins (the basic introduction of DP)
- 综合能力测评系统
- View workflow
- 2/13 review Backpack + monotonic queue variant
猜你喜欢
Le compte racine de la base de données MySQL ne peut pas se connecter à distance à la solution
CADD course learning (8) -- virtual screening of Compound Library
Basic use of MySQL (it is recommended to read and recite the content)

In depth MySQL transactions, stored procedures and triggers
How to realize automatic playback of H5 video
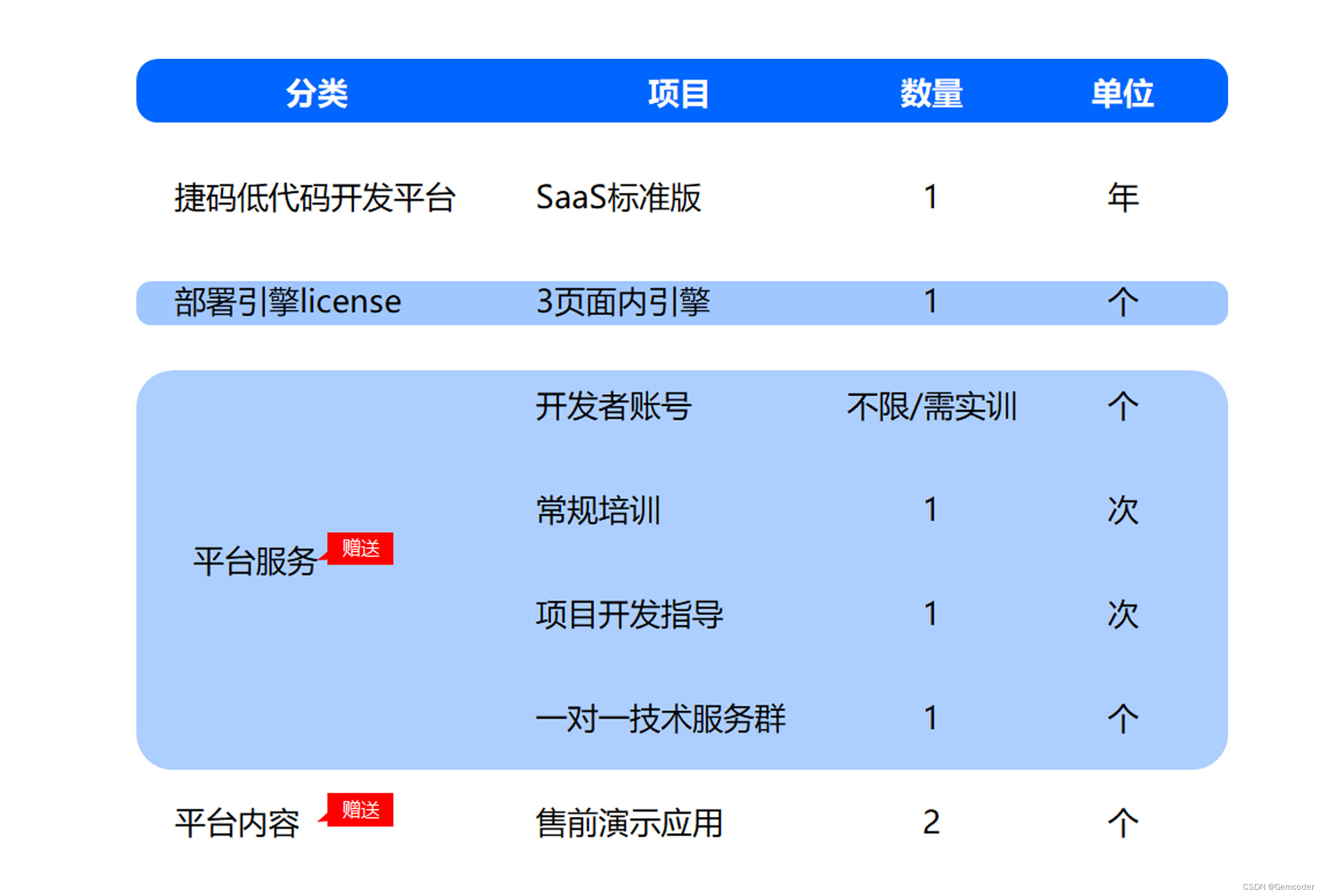
Meet diverse needs: jetmade creates three one-stop development packages to help efficient development
Solutions: word coverage restoration, longest serial number, Xiaoyu buys stationery, Xiaoyu's electricity bill

满足多元需求:捷码打造3大一站式开发套餐,助力高效开发
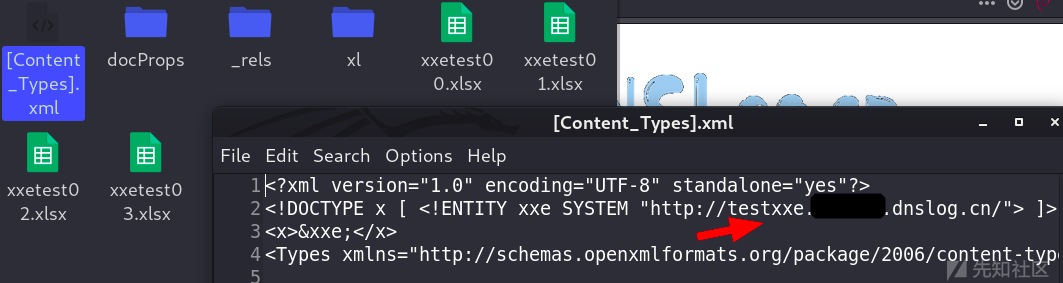
Record an excel xxE vulnerability
图应用详解
随机推荐
Recommendation | recommendation of 9 psychotherapy books
Stable Huawei micro certification, stable Huawei cloud database service practice
Implementation of knowledge consolidation source code 2: TCP server receives and processes half packets and sticky packets
View workflow
Global and Chinese markets for otolaryngology devices 2022-2028: Research Report on technology, participants, trends, market size and share
C. The third problem
综合能力测评系统
How to execute an SQL statement in MySQL
[Zhao Yuqiang] deploy kubernetes cluster with binary package
Crawler notes: improve data collection efficiency! Use of proxy pool and thread pool
查询mysql数据库中各表记录数大小
BOM - location, history, pop-up box, timing
Fedora/rehl installation semanage
VPP performance test
Data processing methods - smote series and adasyn
npm命令--安装依赖包--用法/详解
Yyds dry inventory automatic lighting system based on CC2530 (ZigBee)
JVM garbage collector concept
Global and Chinese markets for patent hole oval devices 2022-2028: Research Report on technology, participants, trends, market size and share
Global and Chinese markets for fire resistant conveyor belts 2022-2028: Research Report on technology, participants, trends, market size and share