当前位置:网站首页>980. Different path III DFS
980. Different path III DFS
2022-07-07 05:53:00 【Empress Yu】
980. Different paths III
On a two-dimensional grid
gridOn , Yes 4 Two types of squares :
1Represents the starting square . And there's only one starting square .2Indicates the end square , And there's only one end square .0An empty square that we can walk through .-1It's an obstacle we can't cross .Return in four directions ( On 、 Next 、 Left 、 Right ) When you go up , The number of different paths from the start square to the end square .
Every barrier free square has to pass once , But you can't go through the same grid repeatedly in a path .
Example 1:
Input :[[1,0,0,0],[0,0,0,0],[0,0,2,-1]] Output :2 explain : We have two paths : 1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2) 2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)Example 2:
Input :[[1,0,0,0],[0,0,0,0],[0,0,0,2]] Output :4 explain : We have four paths : 1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3) 2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3) 3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3) 4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)Example 3:
Input :[[0,1],[2,0]] Output :0 explain : There is no way to go through every empty square completely once . Please note that , The start and end squares can be located anywhere in the grid .Tips :
1 <= grid.length * grid[0].length <= 20
The result of doing the question
success
Method :DFS
1. Find the starting point , Final position , Number of open spaces
2. Start from the starting point and try each path in turn , The occupied space is modified to 1, Try to revert back to 0
class Solution {
public int uniquePathsIII(int[][] grid) {
int[] start = null;
int[] end = null;
int m = grid.length;
int n = grid[0].length;
int empty = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
switch(grid[i][j]){
case 0: {++empty; break;}
case 1: start = new int[]{i,j}; break;
case 2: end = new int[]{i,j}; break;
}
}
}
dfs(start,end,grid,empty);
return ans;
}
int ans = 0;
int[] directions = new int[]{0,1,0,-1,0};
private void dfs(int[] start, int[] end,int[][]grid,int empty){
int m = grid.length;
int n = grid[0].length;
for(int i = 0; i < 4; i++){
int x = start[0]+directions[i];
int y = start[1]+directions[i+1];
if(x>=0&&x<m&&y>=0&&y<n){
if(empty == 0){
if(x==end[0]&&y==end[1])++ans;
}else{
if(grid[x][y]==0){
grid[x][y]=1;
dfs(new int[]{x,y},end,grid,empty-1);
grid[x][y]=0;
}
}
}
}
}
}边栏推荐
- EMMC print cqhci: timeout for tag 10 prompt analysis and solution
- Educational Codeforces Round 22 B. The Golden Age
- R语言【逻辑控制】【数学运算】
- 《2022中国低/无代码市场研究及选型评估报告》发布
- Go language context explanation
- [solved] record an error in easyexcel [when reading the XLS file, no error will be reported when reading the whole table, and an error will be reported when reading the specified sheet name]
- Lombok plug-in
- 消息队列:重复消息如何处理?
- TCC of distributed transaction solutions
- Type de texte de commutation d'entrée et de mot de passe de l'applet natif
猜你喜欢
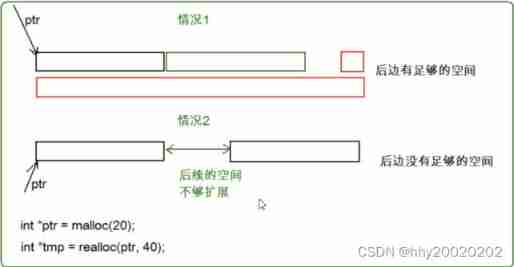
Dynamic memory management
![SQLSTATE[HY000][1130] Host ‘host. docker. internal‘ is not allowed to connect to this MySQL server](/img/05/1e4bdddce1e07f7edd2aeaa59139ab.jpg)
SQLSTATE[HY000][1130] Host ‘host. docker. internal‘ is not allowed to connect to this MySQL server
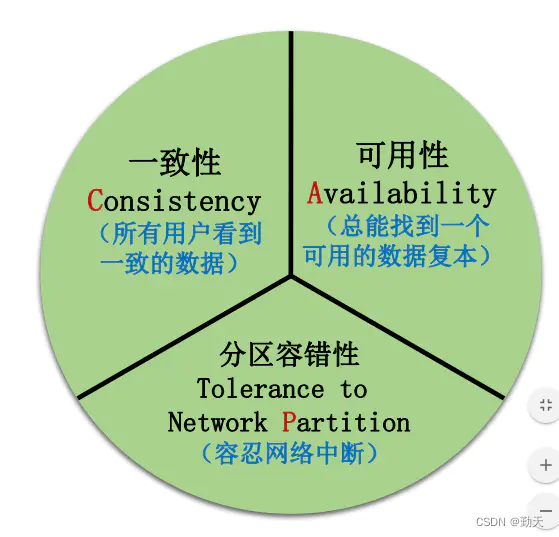
Introduction to distributed transactions

Reading notes of Clickhouse principle analysis and Application Practice (6)
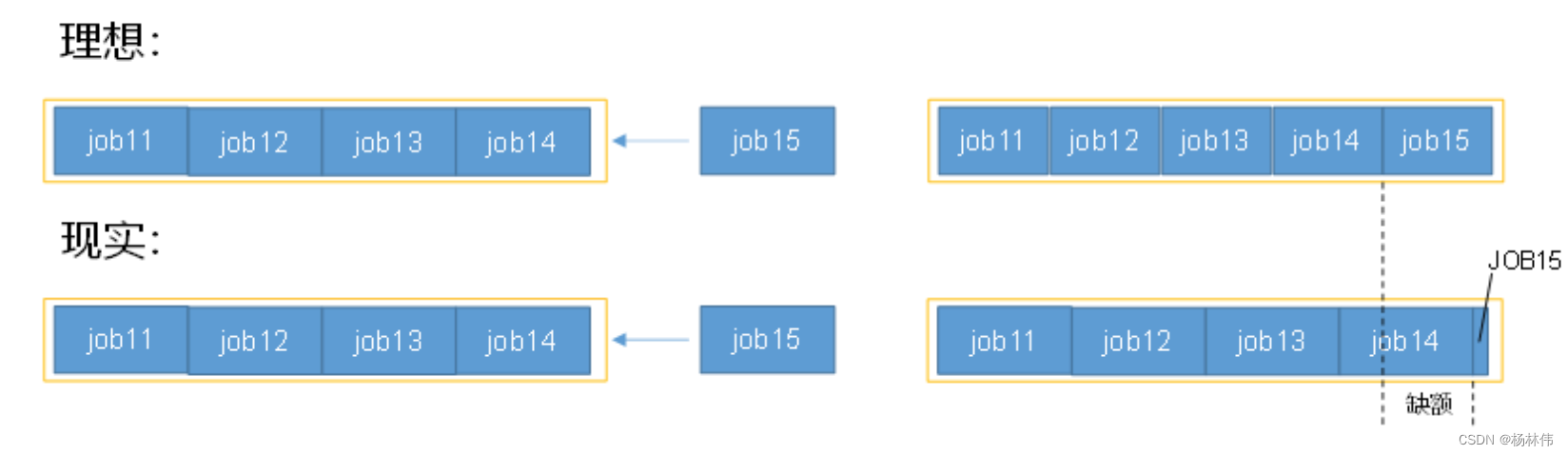
yarn入门(一篇就够了)
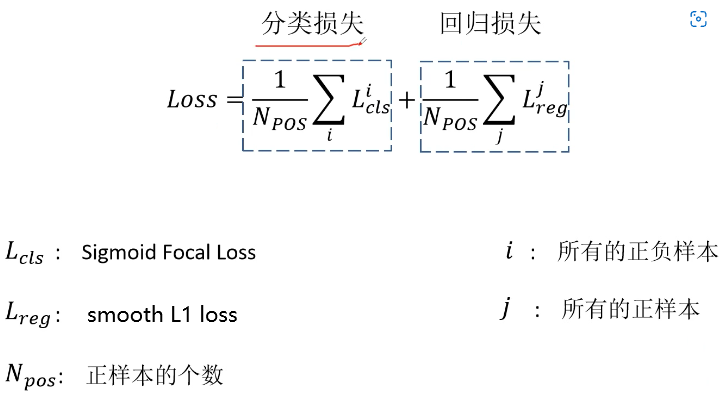
目标检测中的损失函数与正负样本分配:RetinaNet与Focal loss
nVisual网络可视化
爬虫练习题(三)
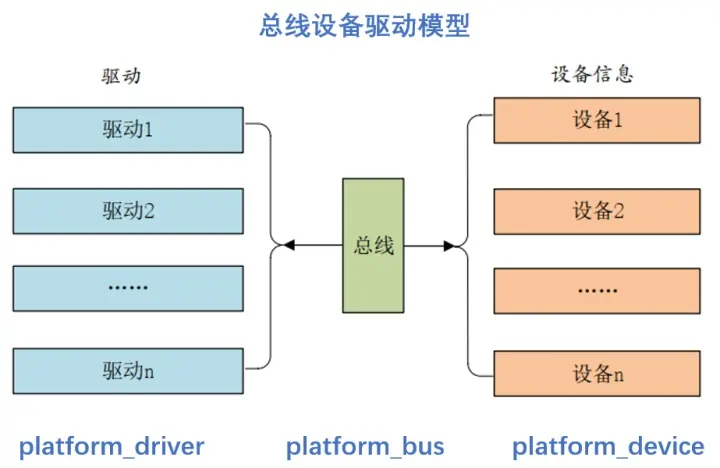
驱动开发中platform设备驱动架构详解
![Paper reading [open book video captioning with retrieve copy generate network]](/img/13/12567c8c2cea2b2a32051535389785.png)
Paper reading [open book video captioning with retrieve copy generate network]
随机推荐
产业金融3.0:“疏通血管”的金融科技
PTA 天梯赛练习题集 L2-002 链表去重
Opensergo is about to release v1alpha1, which will enrich the service governance capabilities of the full link heterogeneous architecture
"Multimodal" concept
On the difference between FPGA and ASIC
win配置pm2开机自启node项目
STM32 key state machine 2 - state simplification and long press function addition
每秒10W次分词搜索,产品经理又提了一个需求!!!(收藏)
SQL query: subtract the previous row from the next row and make corresponding calculations
谈fpga和asic的区别
Common skills and understanding of SQL optimization
目标检测中的BBox 回归损失函数-L2,smooth L1,IoU,GIoU,DIoU,CIoU,Focal-EIoU,Alpha-IoU,SIoU
[shell] clean up nohup Out file
Lombok plug-in
《2022中国低/无代码市场研究及选型评估报告》发布
Add salt and pepper noise or Gaussian noise to the picture
Interview skills of software testing
How to improve website weight
Data storage 3
Go language context explanation