树-二叉搜索树

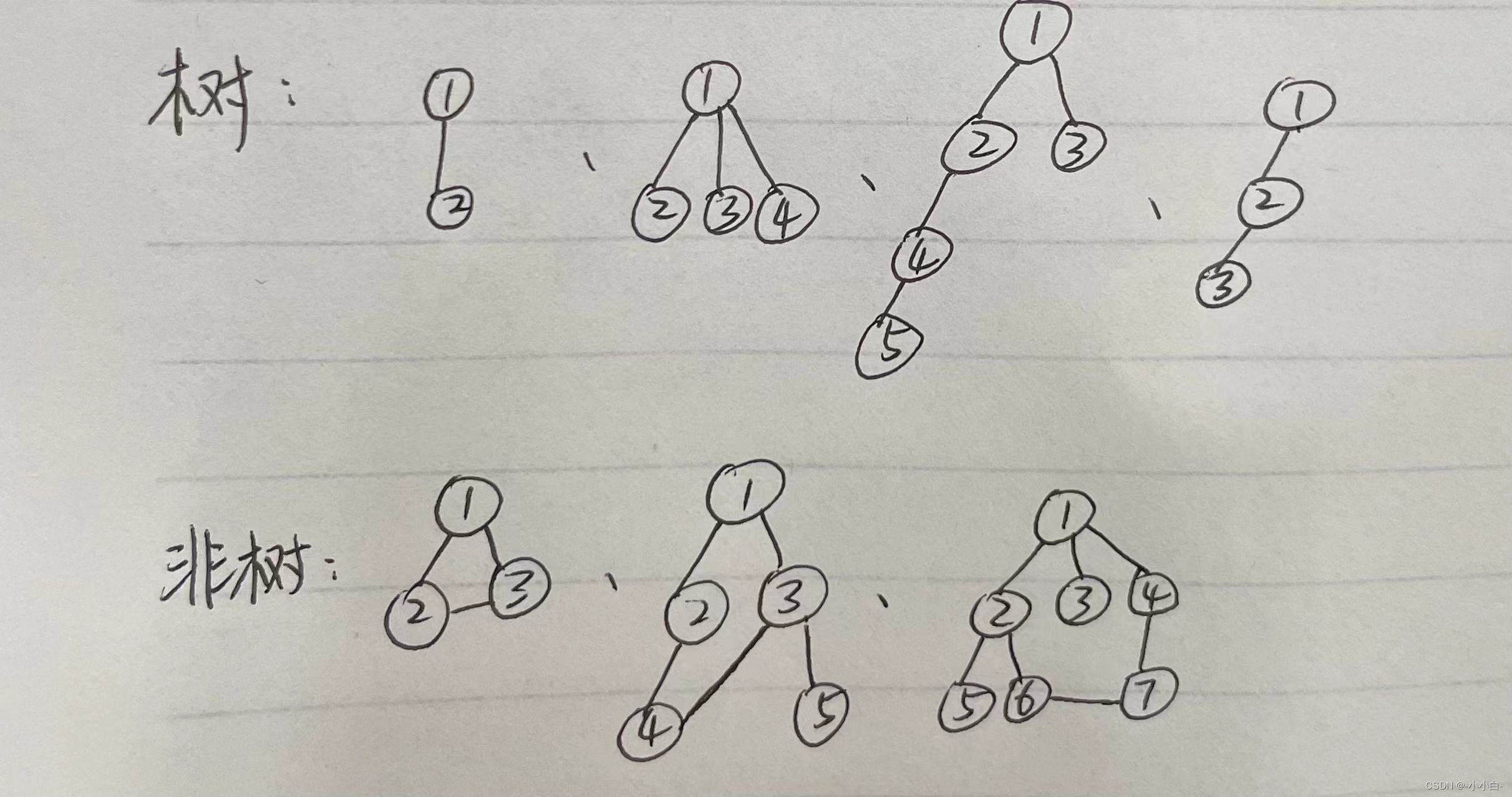
-树是什么

树是计算机中非常重要的一种数据结构，它是由n（n>=1）个有限结点组成的一个具有层次关系的集合。这里只讨论由链表链接的树。

树具有以下特点

 1.每个结点有零个或多个子结点；
 2.没有父结点的结点为根结点；
 3.每一个非根结点只有一个父结点；
 4.每个结点及其后代结点整体上可以看做是一棵树，称为当前结点的父结点的一个子树；

-二叉树

如果一个树的每个结点的子节点不超过两个，则可以说这个树是二叉树.如下图就是一个标准的二叉树。

二叉树的中序遍历

中序遍历：按照访问左子树——根节点——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候，我们按照同样的方式遍历，直到遍历完整棵树。

- 以上图这个树来说，中序遍历的结果应该是DBEAFCG-

递归实现中序遍历（传入根结点）

​void inorder(TreeNode* T)
{
   if(T == NULL){
       return;
   }
   inorder(T->left);
   printf("%d ", T->data);
   inorder(T->right);
}

二叉树的前序遍历

前序遍历：按照访问根节点——左子树——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候，我们按照同样的方式遍历，直到遍历完整棵树。

- 以上图这个树来说，前序遍历的结果应该是ABDECFG-

递归实现中序遍历（传入根结点）

void inorder(TreeNode* T)
{
   if(T == NULL){
       return;
   }
   printf("%d ", T->data);
   inorder(T->left);
   inorder(T->right);
}

二叉树的后序遍历

后序遍历：按照访问左子树——右子树——根节点的方式遍历这棵树，而在访问左子树或者右子树的时候，我们按照同样的方式遍历，直到遍历完整棵树。

- 以上图这个树来说，后序遍历的结果应该是DEBFGCA-

递归实现后序遍历（传入根结点）

​void inorder(TreeNode* T)
{
   if(T == NULL){
       return;
   }
   printf("%d ", T->data);
   inorder(T->left);
   inorder(T->right);
}

用前序遍历的思想创建二叉树

void CreateTree(TreeNode** T)
{
    int num;
    scanf("%d", &num);
    if(num == -1)
        *T = NULL;
    else
    {
        *T=(TreeNode*)malloc(sizeof(TreeNode));
        (*T)->data = num;
        CreateBiTree(&(*T)->left);
        CreateBiTree(&(*T)->right);
    }
}

传入参数为根节点的地址。注意在赋值的时候按照前序遍历的思想根节点——左子树——右子树来赋值，注意空结点不能跳过，需要输入-1（自定义）来表示根结点。

如要创建这个二叉树，需要依次输入A  B  D   -1  -1  E  -1  -1  C  F  -1  -1  G  -1  -1。

二叉搜索（查找）（排序）树

二叉搜索树的节点放置规则是：任何节点的键值一定大于去其左子树中的每一个节点的键值，并小于其右子树的每一个节点的键值。

现有序列：A = {61, 87, 59, 47, 35, 73, 51, 98, 37, 93}。根据此序列构造二叉搜索树过程如下：

（1）i = 0，A[0] = 61，节点61作为根节点；
  （2）i = 1，A[1] = 87，87 > 61，且节点61右孩子为空，故81为61节点的右孩子；
  （3）i = 2，A[2] = 59，59 < 61，且节点61左孩子为空，故59为61节点的左孩子；
  （4）i = 3，A[3] = 47，47 < 59，且节点59左孩子为空，故47为59节点的左孩子；
  （5）i = 4，A[4] = 35，35 < 47，且节点47左孩子为空，故35为47节点的左孩子；
  （6）i = 5，A[5] = 73，73 < 87，且节点87左孩子为空，故73为87节点的左孩子；
  （7）i = 6，A[6] = 51，47 < 51，且节点47右孩子为空，故51为47节点的右孩子；
  （8）i = 7，A[7] = 98，98 < 87，且节点87右孩子为空，故98为87节点的右孩子；
  （9）i = 8，A[8] = 93，93 < 98，且节点98左孩子为空，故93为98节点的左孩子；创建完毕后如图2.4中的二叉搜索树：

 二叉搜索树的创建，插入及删除

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct BSTNode//二叉树结构体 
{
	int data;//数据域
	struct BSTNode *lchild,*rchild;//左右孩子指针 
}BSTNode,*BSTree;

void InitTree(BSTree &T)//初始化二叉排序树 
{
	T = (BSTNode*)malloc(sizeof(BSTNode));//创建一个头结点 
	T->data = 0;
	T->lchild = T->rchild = NULL;//头结点指针域NULL 
}

void InsertTree(BSTree &T,int e)//二叉排序树的插入 
{
	if(!T)//找到插入位置，递归结束 
	{
		BSTree S;
		S = (BSTNode *)malloc(sizeof(BSTNode));//创建一个结点
		S->data = e;//新结点的数据置为e 
		S->lchild = S->rchild = NULL;//新结点设置为叶子结点 
		T = S;//把新结点S接到已找到的插入位置 
	}
	else if(e<T->data)
		InsertTree(T->lchild,e);//将S插入左子树 
	else
		InsertTree(T->rchild,e);//将S插入右子树 
} 

void CreateTree(BSTree &T)//创建二叉排序树 
{
	int a;
	printf("请输入：");
	scanf("%d",&a);
	T->data = a;//将数据填入二叉排序树的根结点 
	while(1)//利用循环进行插入操作 
	{
		scanf("%d",&a);
		InsertTree(T,a);//将数据导入到二叉排序树T中 
		if(getchar()=='\n')//死循环结束条件 
			break;
	}
}

void InOrderTraverse(BSTree T)//遍历二叉树，中序遍历 
{
	if(T)//递归终止条件是T为NULL  
	{
		InOrderTraverse(T->lchild);//中序遍历左子树 
		printf("%d ",T->data);//输出打印根结点 
		InOrderTraverse(T->rchild);//中序遍历右子树 
	}
}

int SearchTree(BSTree T,int key)//二叉排序树的查找，这里的查找只能知道二叉树中有没有和key相等的值 
{
	if(T == NULL)//查找结束，且没有和key相等的值 
		return 0;
	else if(T->data==key)//查找结束，二叉树中有和key相等的值 
		return T->data;	
	else if(key<T->data)
		return SearchTree(T->lchild,key);//递归左子树 
	else
		return SearchTree(T->rchild,key);//递归右子树 
}

void DeleteTree(BSTree &T,int key)//从二叉排序树T中删除关键字等于key的结点  ,这里分三种情况进行讨论 
{
	BSTree f,p;
	p = T;
	f = NULL;//初始化 
	while(p)//利用循环找到关键字等于key的结点
	{
		if(p->data == key)//找到关键字等于key的结点，并跳出循环 
			break;
		f = p;//结点f一直为结点p的双亲结点 
		if(p->data>key)
			p = p->lchild;//在p的左子树中继续查找 
		else
			p = p->rchild;//在p的右子树中继续查找 
	}
	if(p == NULL)//找不到被删除的结点则返回 
	{
		printf("没有找到要删除的值！\n");
		return ; 
	}
	/*第一种情况：被删除的结点（包含被删除的结点是根结点）的左右子树都存在，在其左子树上找中序最后一个结点填补*/ 
	BSTree q,s;
	if((p->lchild)&&(p->rchild))//被删结点p左右子树均不空 
	{
		q = p;
		s = p->rchild;
		while(s->rchild)//在结点p的左子树中继续查找其前驱结点,即最右下结点 
		{
			q = s;
			s = s->rchild;//向右到尽头 
		}
		p->data = s->data;//结点s中的数据顶替被删结点p中的 
		if(q != p)//重新连接结点q的右子树 
			q->rchild = s->lchild;
		else//重新连接结点q的左子树 
			q->lchild = s->lchild;
		free(s);//释放s 
		return ;//结束该函数 
	}
	/*第二种情况：被删结点(包含根结点)缺右子树，且包含左右子树都缺（即叶子结点）；缺右子树用左孩子填补*/
	else if(p->rchild == NULL)//被删结点缺右子树 
	{
		if(f)//判断被删结点是否为根结点，若是则f==NULL 
		{
			if(f->lchild == p)//判断被删结点的双亲结点的左孩子是否为p 
			{
				f->lchild = p->lchild;
				p->lchild = NULL;
			}
			else//被删结点的双亲结点的右孩子为p 
			{
				f->rchild = p->lchild;
				p->lchild = NULL;
			}
			free(p);//释放结点p 
			return ;//结束该函数 
		}
		else//被删结点为根结点 
		{
			f = p;
			p = p->lchild;
			f->lchild = NULL;
			free(f);//释放根结点 
			T = p;//根结点移位 
			return ;
		}
	}
	/*第三种情况：被删结点(包含根结点)缺左子树，且包含左右子树都缺（即叶子结点）；缺左子树用右孩子填补*/
	else	//	else if(p->lchild == NULL)//被删结点缺左子树 
	{
		if(f)//判断被删结点是否为根结点，若是则f==NULL 
		{
			if(f->lchild == p)//判断被删结点的双亲结点的左孩子是否为p 
			{
				f->lchild = p->rchild;
				p->rchild = NULL;
			}
			else//被删结点的双亲结点的右孩子为p 
			{
				f->rchild = p->rchild;
				p->rchild = NULL;
			}
			free(p);//释放结点p
			return ;//结束该函数 
		}
		else//被删结点为根结点 
		{
			f = p;
			p = p->rchild;
			f->lchild = NULL;
			free(f);//释放根结点 
			T = p;//根结点移位 
			return ;//结束该函数 
		}
	}
}

int main()
{
	BSTree T;
	InitTree(T);//初始化二叉排序树 
	CreateTree(T);//创建二叉排序树 
	InOrderTraverse(T);//打印 
	printf("\n");
	if(SearchTree(T,16))//判断二叉排序树中是否存在关键字与key相等的结点 ，其中的16是测试值，可换变量 
		printf("存在：%d\n",SearchTree(T,16));
	else
		printf("不存在！\n"); 
	DeleteTree(T,16);//二叉排序树的删除，删除与key相等的结点，其中的数值为测试值 
	printf("删除之后："); 
	InOrderTraverse(T);//再次打印结果，验证删除是否成功 
	free(T);
	return 0;
}