当前位置:网站首页>2022-08-01 回顾基础二叉树以及操作
2022-08-01 回顾基础二叉树以及操作
2022-08-05 09:04:00 【ShaYQ】
二叉树常被用于实现二叉查找树和二叉堆。
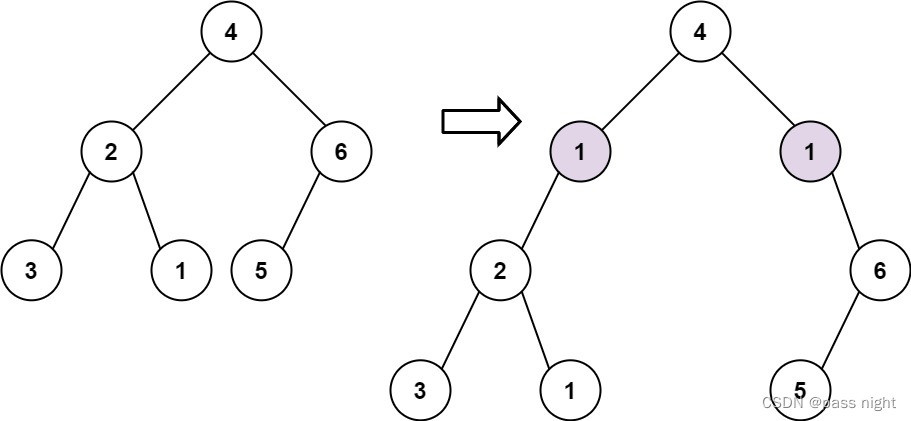
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”。
根据不同的用途可分为:
1、完全二叉树——若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1)
的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。2、满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
3、平衡二叉树——平衡二叉树又被称为AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
/* File: binary_tree.cpp Function: 回顾二叉树的一些操作,创建、销毁、遍历 Writer: syq Time: 2022-08-01 */
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
typedef int KEY_VALUE;
/* 定义二叉树的节点 */
struct BinaryTreeNode
{
struct BinaryTreeNode* m_left;
struct BinaryTreeNode* m_right;
KEY_VALUE m_nKey; //key
};
/* 定义二叉树,二叉树可以从它的根节点进行遍历 */
struct BinaryTree
{
struct BinaryTreeNode* pRoot;
};
/* 创建一个二叉树的节点 */
struct BinaryTreeNode* CreateTreeNode(KEY_VALUE nKey)
{
struct BinaryTreeNode* pNode = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
if(pNode)
{
std::cout<<"create address:"<<pNode<<std::endl;
pNode->m_left = pNode->m_right = nullptr;
pNode->m_nKey = nKey;
return pNode;
}
return nullptr;
}
/* 向一个二叉树中插入一个二叉树节点,如果key已经存在则不需要执行插入 */
int BinaryTreeInsert(struct BinaryTree* pTree,KEY_VALUE nKey)
{
if(pTree == nullptr)
{
return -1;
}
if(pTree->pRoot == nullptr)
{
//根节点为空的时候
pTree->pRoot = CreateTreeNode(nKey);
return 0;
}
//根节点
struct BinaryTreeNode* pRoot = pTree->pRoot;
struct BinaryTreeNode* pTmp = pTree->pRoot;
//进行遍历,同时确定确定插入位置
while(pRoot != nullptr)
{
pTmp = pRoot;
if(nKey < pTmp->m_nKey)
{
//左子树
pRoot = pTmp->m_left;
}
else if(nKey > pTmp->m_nKey)
{
pRoot = pTmp->m_right;
}
}
//pRoot已经为nullptr了,则上一个有效节点是pTmp;
if (nKey < pTmp->m_nKey)
{
pTmp->m_left = CreateTreeNode(nKey);
} else
{
pTmp->m_right = CreateTreeNode(nKey);
}
return 0;
}
/* 销毁m某个节点开始的,二叉子树,采用中序遍历 */
int BinaryTree_Destory(struct BinaryTreeNode* pNode)
{
if (pNode == nullptr) return 0;
BinaryTree_Destory(pNode->m_left);
free(pNode);
std::cout<<"free address:"<<pNode<<std::endl;
BinaryTree_Destory(pNode->m_right);
return 0;
}
/* 二叉树的遍历,前序,中序,后续遍历 前序遍历:先根节点,再左节点,最后右节点 中序遍历:先左节点,再根节点,最后右节点 后序遍历:先左节点,再右节点,最后根节点 */
int BinaryTree_Traversal(struct BinaryTreeNode* pNode)
{
if (pNode == nullptr) return 0;
BinaryTree_Traversal(pNode->m_left);
std::cout << pNode->m_nKey<<std::endl;
BinaryTree_Traversal(pNode->m_right);
return 0;
}
int main()
{
int keyArray[10] = {
1,3,5,6,11,2,4,88,66,55};
struct BinaryTree T = {
0};
int i = 0;
for (i = 0;i < 10;i ++) {
BinaryTreeInsert(&T, keyArray[i]);
}
BinaryTree_Traversal(T.pRoot);
getchar();
BinaryTree_Destory(T.pRoot);
getchar();
}
边栏推荐
- Luogu P1908: 逆序对 [树状数组]
- thinkPHP5 实现点击量(数据自增/自减)
- How to replace colors in ps, self-study ps software photoshop2022, replace one color of a picture in ps with another color
- Three solutions to solve cross-domain in egg framework
- Excuse me, guys, is it impossible to synchronize two databases in real time using Flink SQL CDC?
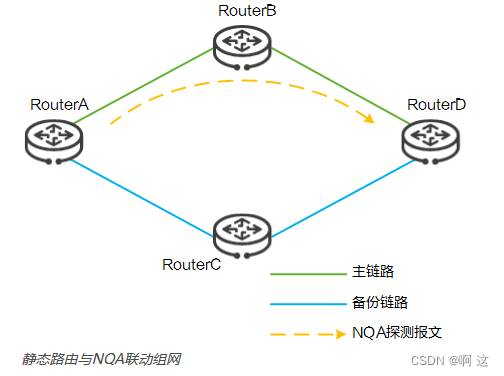
- There is only one switch, how to realize the nqa of master-slave automatic switching
- Thinking after writing a code with a very high CPU usage
- 16 kinds of fragrant rice recipes
- XCODE12 在使用模拟器(SIMULATOR)时编译错误的解决方法
- 【Excel实战】--图表联动demo_001
猜你喜欢
随机推荐
love is a sad song
基于多块信息提取和马氏距离的k近邻故障监测
DPU — 功能特性 — 管理系统的硬件卸载
Pagoda measurement - building small and medium-sized homestay hotel management source code
使用 External Secrets Operator 安全管理 Kubernetes Secrets
How to make a puzzle in PS, self-study PS software photoshop2022, PS make a puzzle effect
只有一台交换机,如何实现主从自动切换之nqa
The Secrets of the Six-Year Team Leader | The Eight Most Important Soft Skills of Programmers
Luogu P3368: 【模板】树状数组 2
spark集群部署(第三弹)
Does flink cdc support synchronization from oracle dg library?
按钮上显示值的轮流切换
【ASM】字节码操作 方法的初始化 Frame
十一道家常小菜详细攻略[图文并茂]
thinkPHP5 realizes clicks (data increment/decrement)
The difference between beautiful MM and ordinary MM
六年团队Leader实战秘诀|程序员最重要的八种软技能 - 脸皮薄容易耽误事 - 自我营销
Excuse me if you want to write data in mysql, with flink - connector - JDBC directly is ok, but I'm in the f
最 Cool 的 Kubernetes 网络方案 Cilium 入门教程
线程之Happens-before规则