当前位置:网站首页>[ACNOI2022]猜数
[ACNOI2022]猜数
2022-07-03 13:25:00 【OneInDark】
题目
题目背景
“阿喏,” O U Y E \sf OUYE OUYE 忽然说,“我们结为兄弟吧!就是那个,作为条件的延伸。因为像我这样的弱者,不报团取暖就很令人生疑……”
D D ( X Y X ) \sf DD(XYX) DD(XYX) 颇吃了一惊。他没有想到事情会进行的这么顺利。
“那好,回家的路上顺便去拜把子吧!”
“只要内卷不止。” O U Y E \sf OUYE OUYE 想。
“只要红石不完。” D D ( X Y X ) \sf DD(XYX) DD(XYX) 想。
—— “便永不分离!” 二人齐声说。
题目描述
交互题。有一个 x ∈ [ 10 , 2 64 − 10 ) x\in[10,\;2^{64}{-}10) x∈[10,264−10) 未知,你来猜。每次可以给出若干区间:
- 若 x x x 在这些区间的并集当中,则交互库有 p = 0.8 p=0.8 p=0.8 的概率返回 1 1 1,有 ( 1 − p ) (1{-}p) (1−p) 概率返回 0 0 0 。
- 否则,交互库必然返回 0 0 0 。
请你用期望最少的次数确定 x x x 。
数据范围与提示
进行 T = 3000 T=3000 T=3000 次测试后,你的平均询问次数不应超过 107 107 107 。
思路
希望你也有 O U Y E \sf OUYE OUYE 一样的慧眼,足以看出关键信息是 每个数成为答案的概率。
我们用 E n t r o p y \rm Entropy Entropy 衡量它,符号为 H H H 。——你不知道信息熵?那你肯定没有看过 3 b 1 b \rm 3b1b 3b1b 教你玩 w o r d l e \rm wordle wordle
突然发现我也不会信息熵,我是小丑。
定义式
H = − ∑ x ∈ U Pr ( x ) log 2 Pr ( x ) H=-\sum_{x\in\Bbb U}\Pr(x)\log_2\Pr(x) H=−x∈U∑Pr(x)log2Pr(x)
其中 U \Bbb U U 是样本空间。下文简记 ω ( x ) = − x log 2 x \omega(x)=-x\log_2 x ω(x)=−xlog2x 。
这个定义非常符合我们的直觉:注意到 ω ( a b ) = b ω ( a ) + a ω ( b ) \omega(ab)=b\omega(a)+a\omega(b) ω(ab)=bω(a)+aω(b),因此有
H = ∑ x ∈ U ω ( Pr [ x ∣ A ] Pr ( A ) ) + ∑ x ∈ U ω ( Pr [ x ∣ ¬ A ] Pr ( ¬ A ) ) = Pr ( A ) H [ A ] + Pr ( ¬ A ) H [ ¬ A ] + ω ( Pr ( A ) ) + ω ( Pr ( ¬ A ) ) \begin{aligned} H&=\sum_{x\in\Bbb U}\omega(\Pr[x\;|\;A]\Pr(A))+\sum_{x\in\Bbb U}\omega(\Pr[x\;|\;\neg A]\Pr(\neg A))\\ &=\Pr(A)H[A]+\Pr(\neg A)H[\neg A]+\omega(\Pr(A))+\omega(\Pr(\neg A)) \end{aligned} H=x∈U∑ω(Pr[x∣A]Pr(A))+x∈U∑ω(Pr[x∣¬A]Pr(¬A))=Pr(A)H[A]+Pr(¬A)H[¬A]+ω(Pr(A))+ω(Pr(¬A))
其中 H [ A ] H[A] H[A] 为 A A A 条件下的熵,即 ∑ x ∈ U ω ( Pr [ x ∣ A ] ) \sum_{x\in\Bbb U}\omega(\Pr[x\;|\;A]) ∑x∈Uω(Pr[x∣A]) 。
也就是说,用 Pr ( A ) \Pr(A) Pr(A) 对应的熵(信息量)知晓 A A A 是否成立,然后往下递归。
考虑询问一个集合 T T T 满足 Pr [ x ∈ T ] = q , H [ x ∈ T ] = h 1 , H [ x ∉ T ] = h 0 \Pr[x\in T]=q,\;H[x\in T]=h_1,\;H[x\notin T]=h_0 Pr[x∈T]=q,H[x∈T]=h1,H[x∈/T]=h0 。询问之后:
- 有 p q pq pq 的概率得到 1 1 1,然后 Pr [ x ∈ T ] = 1 \Pr[x\in T]=1 Pr[x∈T]=1,新的熵 H = h 1 H=h_1 H=h1 。
- 有 ( 1 − p q ) (1-pq) (1−pq) 的概率得到 0 0 0,由贝叶斯公式 Pr [ x ∈ T ∣ 0 ] = Pr [ 0 ∣ x ∈ T ] Pr [ x ∈ T ] Pr [ 0 ] = q − p q 1 − p q \Pr[x\in T\;|\;0]=\frac{\Pr[0\;|\;x\in T]\Pr[x\in T]}{\Pr[0]}=\frac{q-pq}{1-pq} Pr[x∈T∣0]=Pr[0]Pr[0∣x∈T]Pr[x∈T]=1−pqq−pq,新的熵 H = q − p q 1 − p q h 1 + 1 − q 1 − p q h 2 + ω ( q − p q 1 − p q ) + ω ( 1 − q 1 − p q ) H=\frac{q-pq}{1-pq}h_1+\frac{1-q}{1-pq}h_2+\omega({q-pq\over 1-pq})+\omega({1-q\over 1-pq}) H=1−pqq−pqh1+1−pq1−qh2+ω(1−pqq−pq)+ω(1−pq1−q) 。
原本的熵是 q h 1 + ( 1 − q ) h 2 + ω ( q ) + ω ( 1 − q ) qh_1+(1{-}q)h_2+\omega(q)+\omega(1{-}q) qh1+(1−q)h2+ω(q)+ω(1−q) 。因此,期望下得到的信息量是
Δ H = q h 1 + ( 1 − q ) h 2 + ω ( q ) + ω ( 1 − q ) − p q h 1 − ( 1 − p q ) [ q − p q 1 − p q h 1 + 1 − q 1 − p q h 2 + ω ( q − p q 1 − p q ) + ω ( 1 − q 1 − p q ) ] = ω ( q ) + ω ( 1 − q ) − ( 1 − p q ) [ ω ( q − p q 1 − p q ) + ω ( 1 − q 1 − p q ) ] \begin{aligned} \Delta H&=qh_1+(1{-}q)h_2+\omega(q)+\omega(1{-}q)-pqh_1\\ &-(1{-}pq)\left[\frac{q-pq}{1-pq}h_1+\frac{1-q}{1-pq}h_2+\omega\left(\frac{q-pq}{1-pq}\right)+\omega\left(\frac{1-q}{1-pq}\right)\right]\\ &=\omega(q)+\omega(1{-}q)-(1{-}pq)\left[\omega\left(\frac{q-pq}{1-pq}\right)+\omega\left(\frac{1-q}{1-pq}\right)\right] \end{aligned} ΔH=qh1+(1−q)h2+ω(q)+ω(1−q)−pqh1−(1−pq)[1−pqq−pqh1+1−pq1−qh2+ω(1−pqq−pq)+ω(1−pq1−q)]=ω(q)+ω(1−q)−(1−pq)[ω(1−pqq−pq)+ω(1−pq1−q)]
这也是符合我们的直观感受的——内部元素并没有获得区分,因此内部的熵并不会干扰信息量。
利用在线数学工具(考场上建议打表取最优值)可知最优的
q = 5 ( 5 4000 + 3381 5 − 100 5 − 64 ) 2869 q=\frac{5\left(5\sqrt{4000+3381\sqrt{5}}-100\sqrt{5}-64\right)}{2869} q=28695(54000+33815−1005−64)
它约等于
q ≈ 0.4356636377796835808889 q\approx 0.4356636377796835808889 q≈0.4356636377796835808889
取 q = 0.435 q=0.435 q=0.435 计算,期望 Δ H ≈ 0.618 \Delta H\approx 0.618 ΔH≈0.618 。多么美丽的数字。因此期望下经过 64 Δ H ≈ 103.56 \frac{64}{\Delta H}\approx 103.56 ΔH64≈103.56 次询问后可以出解。
代码
- 因为是期望询问次数,不能用尽 107 107 107 次询问就收,而是出解就 r e t u r n \tt return return 。
- 由于数字多达 2 64 2^{64} 264 个,过程中真实答案的 Pr \Pr Pr 可能降到很低,请不要放弃它!
- 时间复杂度不太好算。但可以想到的是:区间数量是比较少的,约为 64 64 64 个。
#include "guess.h"
#include <cstdio>
#include <algorithm> // Almighty XJX yyds!!!
#include <cstring> // oracle: ZXY yydBUS!!!
#include <cctype> // Huge Egg Dog eats me!!!
#include <vector>
#include <utility>
#include <cmath>
using llong = long long;
# define rep(i,a,b) for(int i=(a); i<=(b); ++i)
# define drep(i,a,b) for(int i=(a); i>=(b); --i)
# define rep0(i,a,b) for(int i=(a); i!=(b); ++i)
inline int readint(){
int a = 0, c = getchar(), f = 1;
for(; !isdigit(c); c=getchar()) if(c == '-') f = -f;
for(; isdigit(c); c=getchar()) a = a*10+(c^48);
return a*f;
}
using ullong = unsigned long long;
using PUU = std::pair<ullong,ullong>;
extern bool Query(std::vector<PUU> v);
bool query(std::vector<PUU> v){
for(PUU &rg : v) -- rg.second;
return Query(v); // close range
}
using ldb = long double;
using NODE = std::pair<PUU,ldb>;
bool cmp(const NODE &a, const NODE &b){
return a.second/(a.first.second-a.first.first)
> b.second/(b.first.second-b.first.first);
}
ullong Guess(){
static const ullong MAXX = 18446744073709551606ull;
std::vector<NODE> v; v.resize(1);
v[0] = NODE{
PUU{
10,MAXX},1};
const long double q = 0.435, p = 0.8, notp = 0.2;
while(true){
if(v[0].first.second == v[0].first.first+1
&& int(v.size()) == 1) return v[0].first.first;
std::vector<PUU> ask; ask.clear();
long double nowq = 0;
for(const NODE &rg : v){
if(nowq >= q) break; // enough
if(nowq+rg.second <= q){
nowq += rg.second; // good
ask.push_back(rg.first); continue;
}
ullong len = rg.first.second-rg.first.first;
ullong cnt = ullong(floor((q-nowq)*len/rg.second));
if(nowq == 0 && cnt == 0) cnt = 1;
if(!cnt) continue; // length = 0
nowq += cnt*rg.second/len; ask.push_back(
PUU{
rg.first.first,rg.first.first+cnt});
}
if(query(ask)){
const int lenask = int(ask.size());
for(int i=0,j=0,k=0; true; ++i){
if(j == lenask){
v.resize(k); break; }
if(ask[j] == v[i].first) // covered
v[k] = v[i], v[k++].second /= nowq, ++ j;
else if(ask[j].first == v[i].first.first){
ullong nxt = ask[j].second-ask[j].first;
ullong now = v[i].first.second-v[i].first.first;
v[k++] = NODE{
ask[j++],v[i].second/nowq*nxt/now};
}
}
}
else{
long double wxk = 1-p*nowq;
const int lenask = int(ask.size()), lenv = int(v.size());
for(int i=0,j=0; i!=lenv; ++i){
v[i].second /= wxk;
if(j == lenask) continue;
if(ask[j] == v[i].first)
v[i].second *= notp, ++ j;
else if(ask[j].first == v[i].first.first){
ullong nxt = ask[j].second-ask[j].first;
ullong now = v[i].first.second-v[i].first.first;
v.push_back(NODE{
ask[j],v[i].second*notp*nxt/now});
v[i].first.first = ask[j++].second; // outside
v[i].second = v[i].second*(now-nxt)/now;
}
}
}
if(true){
// will this be slow?
std::sort(v.begin(),v.end(),cmp);
long double tot = 0;
for(const NODE &rg : v) tot += rg.second;
for(NODE &rg : v) rg.second /= tot;
}
}
}
边栏推荐
- ThreadPoolExecutor realizes multi-threaded concurrency and obtains the return value (elegant and concise way)
- Comprehensively develop the main channel of digital economy and digital group, and actively promote the utonmos digital Tibet market
- 软件测试工作那么难找,只有外包offer,我该去么?
- [quantitative trading] permanent portfolio, turtle trading rules reading, back testing and discussion
- Screenshot of the operation steps of upload labs level 4-level 9
- Resource Cost Optimization Practice of R & D team
- 项目协作的进度如何推进| 社区征文
- 记录关于银行回调post请求405 问题
- 研发团队资源成本优化实践
- When updating mysql, the condition is a query
猜你喜欢

使用Tensorflow进行完整的深度神经网络CNN训练完成图片识别案例2
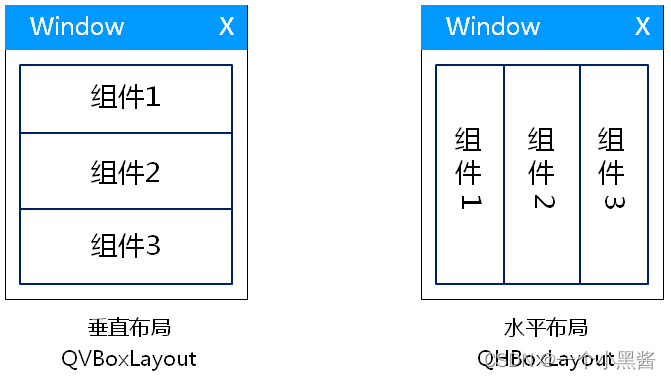
Qt学习22 布局管理器(一)

Use and design of Muduo buffer class
![[技术发展-24]:现有物联网通信技术特点](/img/f3/a219fe8e7438b8974d2226b4c3d4a4.png)
[技术发展-24]:现有物联网通信技术特点
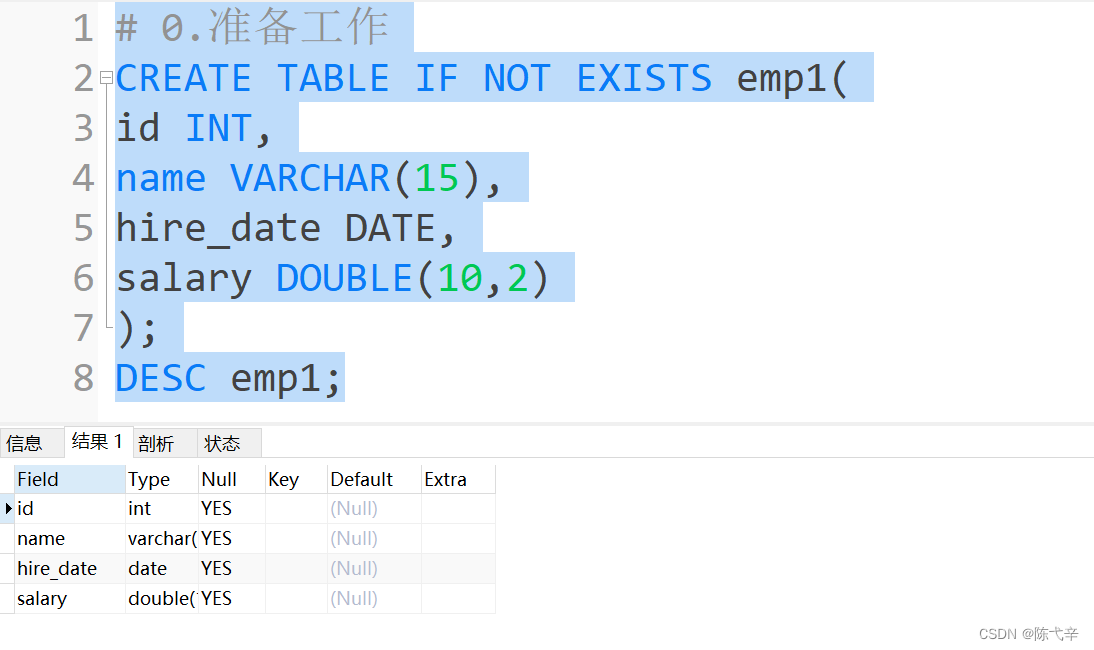
MySQL data processing value addition, deletion and modification
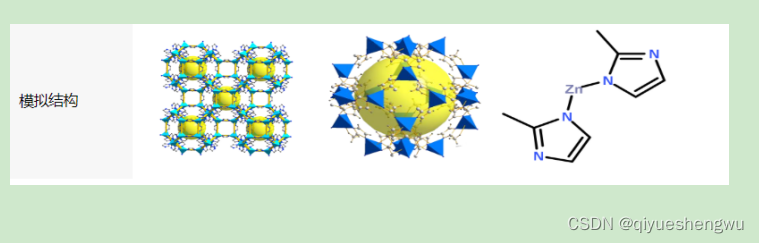
金属有机骨架MOFs装载非甾体类抗炎药物|ZIF-8包裹普鲁士蓝负载槲皮素(制备方法)

解决MySql 1045 Access denied for user ‘root‘@‘localhost‘ (using password: YES)
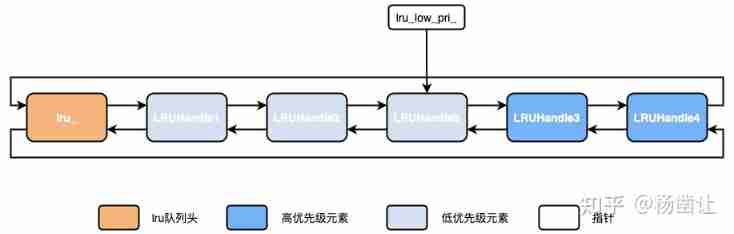
RocksDB LRUCache
Unity EmbeddedBrowser浏览器插件事件通讯

SQL Injection (POST/Select)
随机推荐
Qt学习17 对话框及其类型
Unity embeddedbrowser browser plug-in event communication
怎样删除对象的某个属性或⽅法
Leetcode-1175.Prime Arrangements
Uniapp skills - dom display and hiding
Uniapp skills - scrolling components -1
Software testing is so hard to find, only outsourcing offers, should I go?
PHP maze game
挡不住了,国产芯片再度突进,部分环节已进到4nm
There is nothing new under the sun. Can the meta universe go higher?
树的深入和广度优先遍历(不考虑二叉树)
Windos creates Cordova prompt because running scripts is prohibited on this system
Error handling when adding files to SVN:.... \conf\svnserve conf:12: Option expected
Golang — 命令行工具cobra
使用vscode查看Hex或UTF-8编码
Spring cup eight school league
Libuv Library - Design Overview (Chinese version)
MapReduce implements matrix multiplication - implementation code
Halcon combined with C # to detect surface defects -- Halcon routine autobahn
The latest BSC can pay dividends. Any B usdt Shib eth dividend destruction marketing can