当前位置:网站首页>【R语言数据科学】:交叉验证再回首
【R语言数据科学】:交叉验证再回首
2022-07-04 12:48:00 【JoJo的数据分析历险记】
【R语言数据科学】:交叉验证再回首
- 个人主页:JoJo的数据分析历险记
- 个人介绍:小编大四统计在读,目前保研到统计学top3高校继续攻读统计研究生
- 如果文章对你有帮助,欢迎
关注、点赞、收藏、订阅专栏- 本文收录于【R语言数据科学】本系列主要介绍R语言在数据科学领域的应用包括:
R语言编程基础、R语言可视化、R语言进行数据操作、R语言建模、R语言机器学习算法实现、R语言统计理论方法实现。本系列会坚持完成下去,请大家多多关注点赞支持,一起学习~,尽量坚持每周持续更新,欢迎大家订阅交流学习!

前言
交叉验证可用于计算给定统计学习方法相关的测试误差,以评估其性能,或选择适当的灵活性水平,进行超参数调整。 评估模型性能的过程称为模型评估,而模型评估为模型选择适当的灵活性水平的过程称为模型选择。上一章中,我们讨论了训练集和测试集。我们往往更关注模型在测试集上的误差(测试误差)。测试误差是统计学习方法对新数据集预测所产生的平均误差。 在给定的数据集下,如果某一特定的统计学习方法测试误差很低,那么这个模型的效果还不错。相比之下,训练误差是比较容易得到和控制的。训练误差通常与测试误差有很大不同,往往训练误差要大于测试误差。在没有可用于直接估计测试误差测试集的情况下,可以使用多种数学技巧调整训练误差,来估计测试误差。之后我们再详细介绍。在这一章中,我们考虑了将数据集划分的方法。我们需要对数据集划分:训练集、验证集、测试集。有时将验证集和测试集放在一起)常见的交叉验证方法有2个:
- K折交叉验证
- 留一法交叉验证
1 K折交叉验证
我们第一个讨论的是K 折交叉验证。一般来说,机器学习挑战始于一个数据集(下图中的蓝色)。我们需要使用该数据集构建一个算法,该算法最终将用于完全独立的数据集(黄色)。
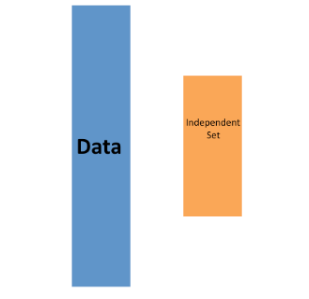
但是在实际情况中,我们不知道黄色的数据集。
因此,为了模拟这种情况,我们分割出一部分数据集并假装它是一个独立的数据集,如下图所示我们将数据集分为训练集(蓝色) 和测试集(红色)。我们将专门在训练集上训练我们的算法,并将测试集仅用于评估目的。
我们通常会尝试选择一小部分数据集作为测试集,以便我们有尽可能多的数据进行训练。但是,我们也希望测试集足够大,这样我们就可以在不拟合不切实际的模型数量的情况下获得稳定的损失估计。典型的选择是使用 20%-30% 的数据作为测试集。当然在现在有的数据量上千万时,可能选用更小的比例。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pdGV1xio-1656858582711)(https://s2.loli.net/2022/07/03/PfUQqM7yVFx9sGL.png)]](/img/85/03960fd63da4798abd2a6f0e74d3fc.png)
现在在这提出了一个新问题,因为对于大多数机器学习算法,我们需要选择超参数。例如KNN算法中的k。这些参数不是模型训练得出来的,也就是我们常常说的调参部分的超参数,我们需要在不使用我们的测试集的情况下优化算法参数,我们知道如果我们在同一个数据集上优化和评估,很容易过拟合(Overfitting)。这是交叉验证最有用的地方。对于每组算法参数,我们需要一个 MSE 的估计值,然后我们将选择具有最小 MSE 的超参数 λ \lambda λ。
M S E ( λ ) = 1 k ∑ i = 1 k 1 n ∑ i = 1 n ( y i ^ ( λ ) − y i ) 2 MSE(\lambda) = \frac{1}{k}\sum_{i=1}^{k}\frac{1}{n}\sum_{i=1}^{n}(\hat{y_i}(\lambda)-y_i)^2 MSE(λ)=k1i=1∑kn1i=1∑n(yi^(λ)−yi)2
其中k表示交叉验证的次数,n表示样本量
现在我们可以把训练集进一步划分为训练集和验证集,我们在训练集上拟合模型,然后计算在验证集上的MSE,如下图所示
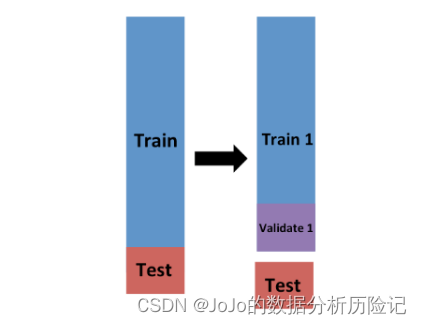
计算
Validate1上的MSE:
M S E ( λ ) = 1 m ∑ i = 1 m ( y i ^ ( λ ) − y i ) 2 MSE(\lambda) = \frac{1}{m}\sum_{i=1}^{m}(\hat{y_i}(\lambda)-y_i)^2 MSE(λ)=m1i=1∑m(yi^(λ)−yi)2
其中m表示每个验证集上的样本
注意:上述我们只是计算了一个验证集上的MSE,为了提高泛化性,我们设置了k个验证集,我们首先整体训练集分为k个不相交的集合,每次选取其中一个集合作为验证集,k-1个作为训练集,然后我们得到 M S E 1 , . . . , M S E k MSE_1,...,MSE_k MSE1,...,MSEk,然后计算他们的平均值:
M S E ( λ ) = 1 k ∑ i = 1 k M S E i ( λ ) MSE(\lambda) = \frac{1}{k}\sum_{i=1}^{k}MSE_i(\lambda) MSE(λ)=k1i=1∑kMSEi(λ)
我们的目标就是让这个平均的MSE最小

现在我们已经描述了如何使用交叉验证来优化参数从而选择模型。但是,我们现在必须考虑到上述优化是发生在训练数据上的事实,因此我们需要根据未用于优化选择的数据来估计最终算法。这是我们使用早期分离的测试集的地方:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AUyEOAWo-1656858582712#pic_center)(https://s2.loli.net/2022/07/03/aehYS8XZutK4W7r.png)]](/img/ea/4a523dec9f706842318c56f3259c33.png)
我们可以再次进行交叉验证:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Mj0Noh3S-1656858582712)(https://s2.loli.net/2022/07/03/Krce4QBj6AqxW5w.png)]](/img/ba/6eba2e176f43213bced56d4828fb3d.png)
在有了测试集之后,我们可以将该测试集进行评估。K折交叉验证的思路是将数据集随机平均的分为K组。第一组作为测试集,剩下的k-1组作为训练集。 M S E 1 MSE_1 MSE1可以看做是第一次训练时,测试组的平均误差。重复k次,我们可以得到k-折交叉验证的测试误差:
C V ( k ) = 1 k ∑ i = 1 k M S E i . CV_{(k)}=\frac{1}{k}\sum_{i=1}^{k}MSE_i. CV(k)=k1i=1∑kMSEi.
并获得我们预期损失的最终估计。但是,请注意,这意味着我们的整个计算时间乘以k。因为我们正在执行许多复杂的计算。因此,我们需要寻找减少时间的方法。对于最终评估,我们通常只使用一个测试集。
一旦我们通过交叉验证确定了最终的模型,我们就可以在整个数据集上重新拟合该模型,而无需更改优化参数。这样我们相当于有了更多的训练数据。这样是有一定效果的,尤其是数据量不大的情况下。
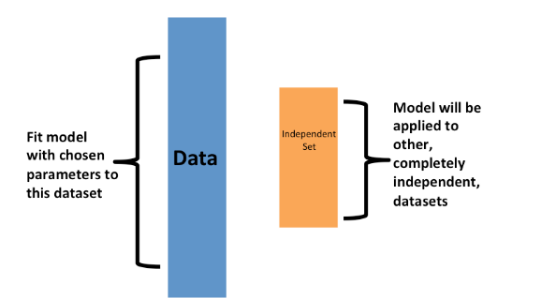
现在我们需要考虑的一个问题是如何选择K? 经过大量的尝试和经验,目前比较常用的选择是
10或5,这也是r和python默认的折数
2 K-fold交叉验证代码实现
cv.glm()函数可以实现k折交叉验证,下面我们使用k=10,也是我们常用的一个k值。我们重新设置随机种子数,在Auto数据集拟合模型,分别拟合了一次到十次多项式回归
# 7是我的幸运数字,我就这么设置了
library(ISLr2)
library(boot)
set.seed(7)
# 初始化向量来保存10折交叉验证的结果
cv_error_10 <- rep(0,10)
for (i in 1:10){
glm.fit <- glm(mpg~poly(horsepower,i), data = Auto)
cv_error_10[i] <- cv.glm(Auto,glm.fit,K = 10)$delta[1]
}
cv_error_10
得到各个模型的误差:
- 24.1463716629577
- 19.3130825829741
- 19.434897545051
- 19.5493689322887
- 19.0736379228708
- 18.7058531603005
- 19.2522869995751
- 18.8552270777634
- 18.9304332711781
- 20.4425474405408
对结果进行可视化
x <- seq(1,10)
library(ggplot2)
kcv <- data.frame(x,cv=cv_error_10)
ggplot(kcv, aes(x, cv)) +geom_point() + geom_line(lwd=1,col='blue')
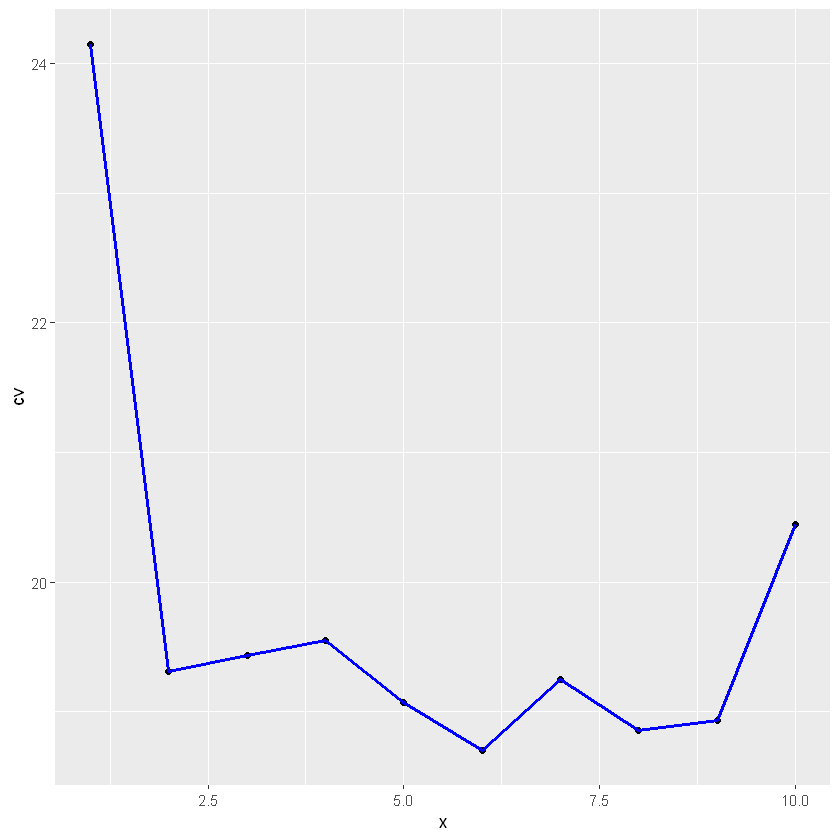
可以看出2次拟合正确率提升较高,可以看出在二次拟合正确率提升较高,再更高次的拟合没有明显的提升模型正确率
3.留一法交叉验证(LOOCV)
留一法交叉验证可以看做是上述方法的一种变换。同样将数据集分为两部分,一部分作为验证集,一部分作为训练集,不同的是,我们在这里不选择相同样本量作为验证集,而仅仅选择一个样本 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)作为验证集。剩下的n-1个样本作为训练集: ( x 2 , y 2 ) , . . . , ( x n , y n ) {(x_2,y_2),...,(x_n,y_n)} (x2,y2),...,(xn,yn),拟合模型
我们相当于做了n次模型训练,然后将这n次拟合的平均测试误差来估计某一个具体模型的测试误差。第一次训练得到的测试误差为: M S E 1 = ( y 1 − y ^ 1 ) 2 MSE_1=(y_1-\hat{y}_1)^2 MSE1=(y1−y^1)2。重复n次得到: M S E 2 , . . . , M S E n MSE_2,...,MSE_n MSE2,...,MSEn。最后我们取平均值得到LOOCV估计的测试MSE:
C V ( n ) = 1 n ∑ i = 1 n M S E i . CV_{(n)}=\frac{1}{n}\sum_{i=1}^{n}MSE_i. CV(n)=n1i=1∑nMSEi.
LOOCV主要有以下几点优势:
- 1.偏差更小,因为我们使用了更多的数据集进行训练
- 2.不会受到抽样的随机性带来的影响。
留一法交叉验证是一个很general的方法,例如在logistic regression或者naive bayes中都可以运用。
留一法交叉验证有一个缺点是计算量较大,因为我们要拟合n次模型。在现在一些问题中,数据量动不动就几G甚至更大,这时拟合模型会花费太多的时间。这相较于k折交叉验证是一个较为明显的缺点。
4.留一法交叉验证代码实现
loocv的结果可以直接使用glm()函数和cv.glm()函数得到。之前我们使用glm()函数拟合了logistic回归,还记得我们使用了family参数=binomal,如果我们不指定family值,则其默认是线性回归,和lm()函数一样。下面我们使用glm()和cv.glm()来实现LOOCV,首先导入boot包
library(boot)
glm.fit <- glm(mpg~horsepower, data = Auto)
cv.err <- cv.glm(Auto,glm.fit)
cv.err$delta
- 24.2315135179292
- 24.2311440937562
可以看出上述得到的两个MSE几乎是一致的,因为LOOCV几乎每一次训练的结果差不多。注意,在使用cv.glm()时,不需要再指定train,会自动实现LOOCV过程。下面我们来看一下不同次方的多项式结果
cv.error <- rep(0,10)
for (i in 1:10) {
glm.fit <- glm(mpg~poly(horsepower,i),data= Auto)
cv.error[i] <- cv.glm(Auto, glm.fit)$delta[1]
}
cv.error
- 24.2315135179293
- 19.2482131244897
- 19.334984064029
- 19.4244303104303
- 19.0332138547041
- 18.9786436582254
- 18.8330450653183
- 18.9611507120531
- 19.0686299814599
- 19.490932299334
结果表明在二次拟合的时候错误率降低较大,这一点和K折交叉验证一致
下面我们将结果进行可视化
loocv <- data.frame(x,cv=cv.error)
library(ggplot2)
ggplot(loocv, aes(x, cv.error)) +geom_point() + geom_line(lwd=1,col='blue')
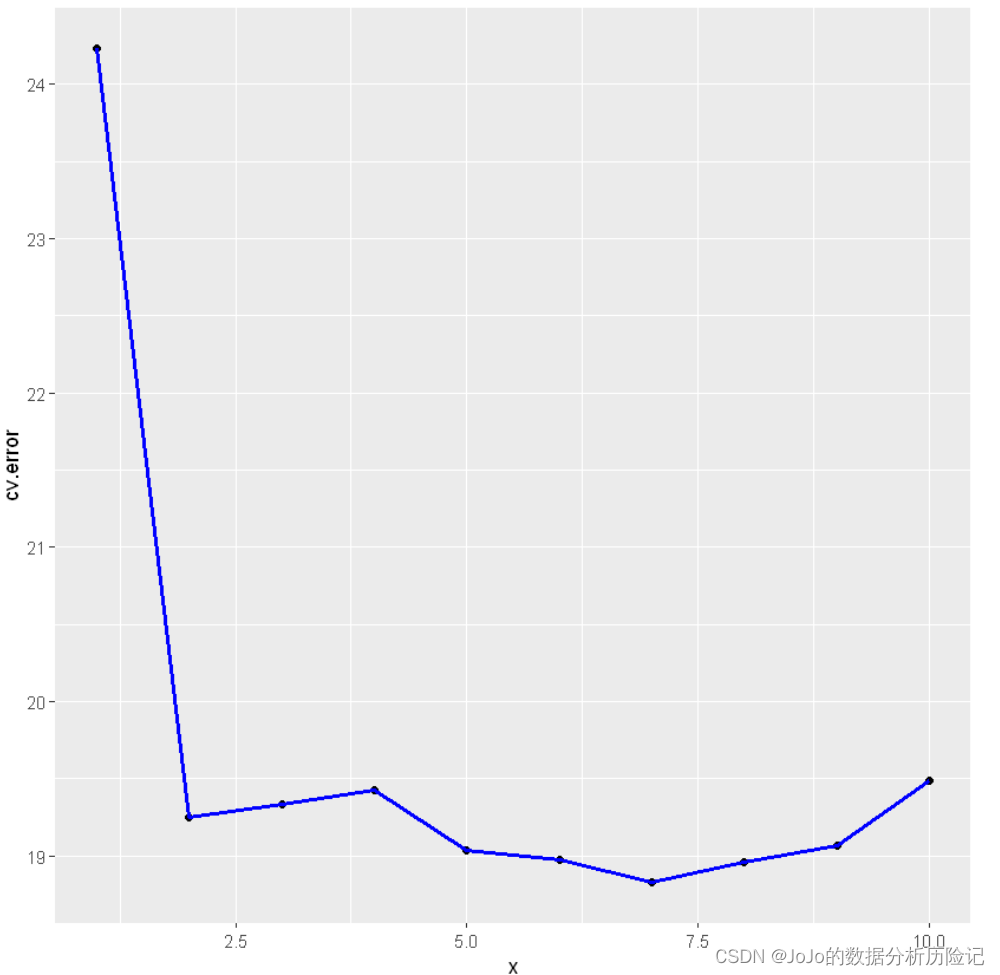
5.总结
我们上面说K折交叉验证在运算上比留一法交叉验证要好。但除去运算量不考虑,另一个比较重要的优势是通常k折交叉验证对测试误差的估计比留一法交叉验证更准确。
我们之前讨论过,留一法交叉验证几乎是无偏的, 因为他用了n-1个数据训练。同样的k折交叉验证无论是k=5和k=10都会导致一定的偏差。如果仅仅从偏差的角度来看,留一法似乎表现的更好。但是我们还要考虑方差的问题。对于LOOCV,我们实际上是在平均拟合模型的输出,每个模型都是在几乎相同的观测集上训练的;因此,这些输出彼此高度(正)相关。相比之下,当我们在k<n的情况下执行K折CV时,我们是对相互之间的相关性较小的k个拟合模型的输出进行平均。因为每个模型的训练集重合度较小。因此LOOCV会有较大的方差。改善估计方差的一种方法是获取更多样本。为此,我们不再需要将训练集划分为非重叠集。相反,我们会选择随机K个大小相同的集合。
总的来说,K折交叉验证取k=5或k=10是一个还不错的水平,方差和偏差都不大。
本章的介绍到此介绍,如果文章对你有帮助,请多多点赞、收藏、评论、关注支持!!
边栏推荐
- SQL language
- In 2022, it will be es2022 soon. Do you only know the new features of ES6?
- Scripy framework learning
- CANN算子:利用迭代器高效实现Tensor数据切割分块处理
- Dgraph: large scale dynamic graph dataset
- 易周金融 | Q1保险行业活跃人数8688.67万人 19家支付机构牌照被注销
- 高质量软件架构的唯一核心指标
- Haproxy high availability solution
- 基于链表管理的单片机轮询程序框架
- A data person understands and deepens the domain model
猜你喜欢

SCM polling program framework based on linked list management

2022kdd pre lecture | 11 first-class scholars take you to unlock excellent papers in advance
Animation and transition effects
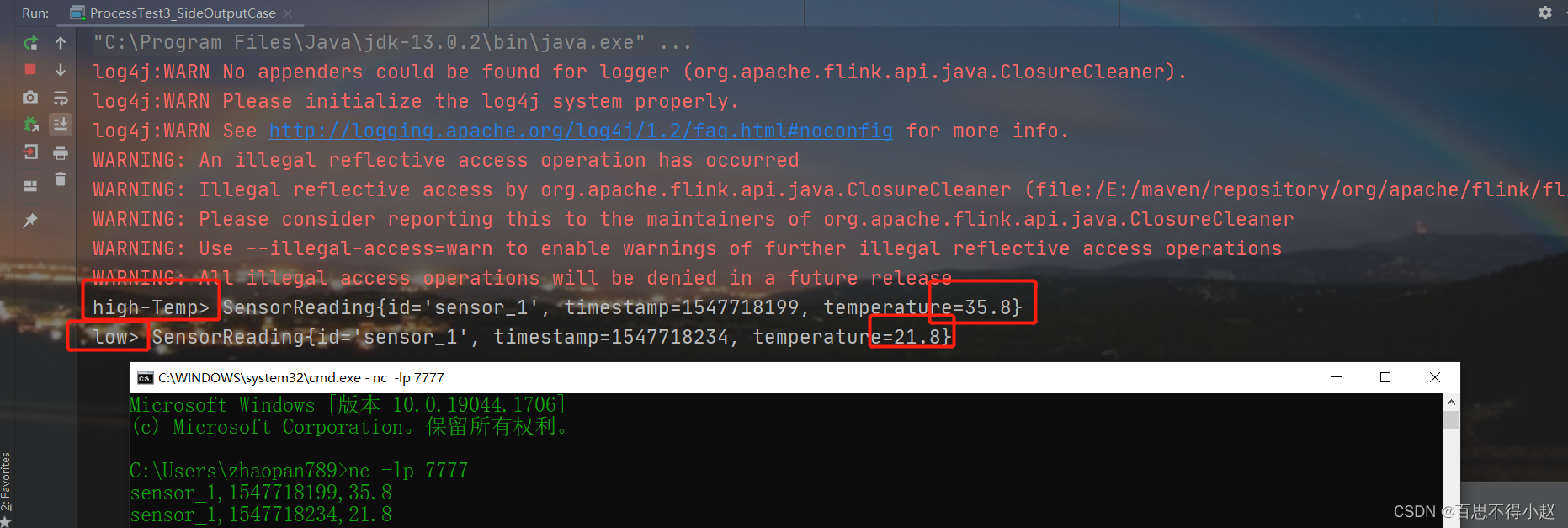
结合案例:Flink框架中的最底层API(ProcessFunction)用法

Flet教程之 03 FilledButton基础入门(教程含源码)(教程含源码)
Openharmony application development how to create dayu200 previewer
Personalized online cloud database hybrid optimization system | SIGMOD 2022 selected papers interpretation

免费、好用、强大的轻量级笔记软件评测:Drafts、Apple 备忘录、Flomo、Keep、FlowUs、Agenda、SideNote、Workflowy

上汽大通MAXUS正式发布全新品牌“MIFA”,旗舰产品MIFA 9正式亮相!
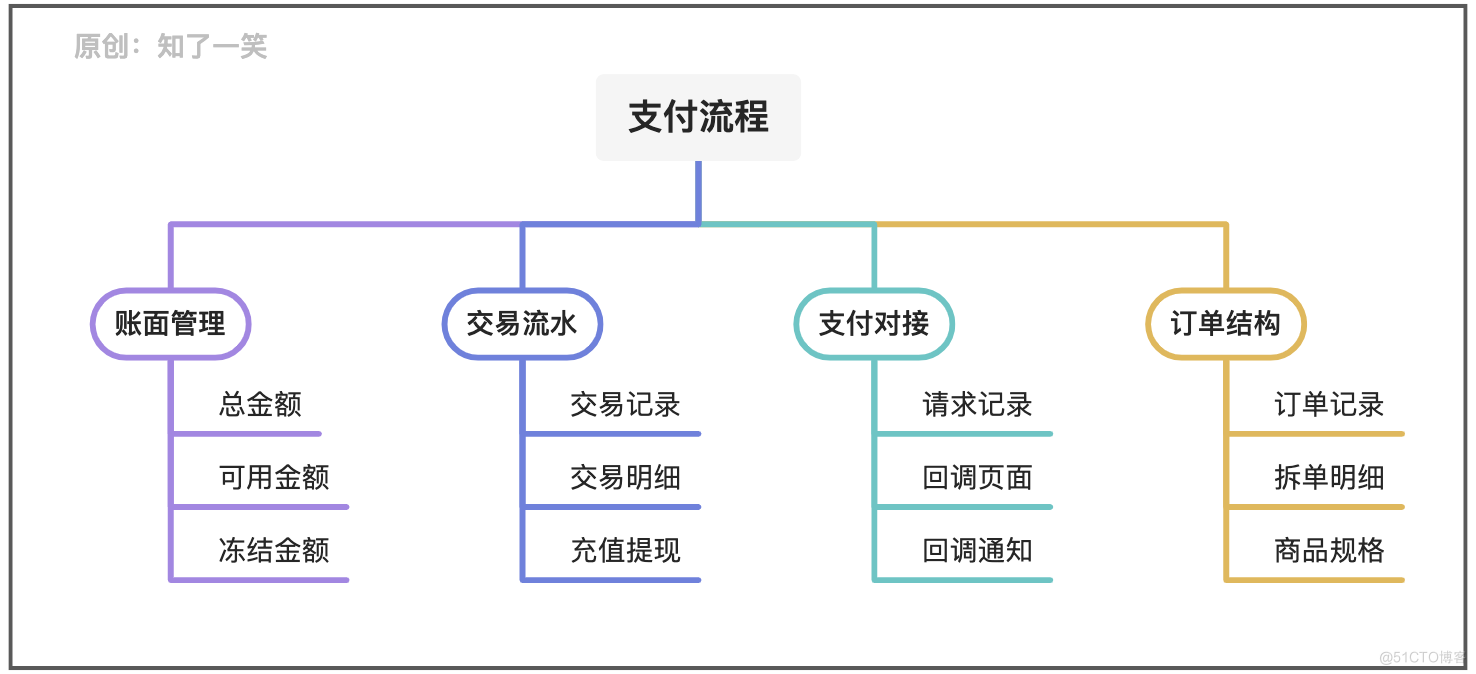
聊聊支付流程的设计与实现逻辑
随机推荐
C语言图书租赁管理系统
OpenHarmony应用开发之如何创建DAYU200预览器
remount of the / superblock failed: Permission denied
SQL language
SQL语言
分布式BASE理论
[FAQ] summary of common causes and solutions of Huawei account service error 907135701
2022G3锅炉水处理考试题模拟考试题库及模拟考试
CA: efficient coordinate attention mechanism for mobile terminals | CVPR 2021
Building intelligent gray-scale data system from 0 to 1: Taking vivo game center as an example
Rsyslog configuration and use tutorial
高质量软件架构的唯一核心指标
Apache服务器访问日志access.log设置
How real-time cloud interaction helps the development of education industry
Besides, rsync+inotify realizes real-time backup of data
Web知识补充
DGraph: 大规模动态图数据集
美国土安全部部长警告移民“不要踏上危险的旅程”
WS2811 M是三通道LED驱动控制专用电路彩灯带方案开发
ASP. Net core introduction I