当前位置:网站首页>【LeetCode】486-预测赢家
【LeetCode】486-预测赢家
2022-07-02 12:09:00 【酥酥~】
给你一个整数数组 nums 。玩家 1 和玩家 2 基于这个数组设计了一个游戏。
玩家 1 和玩家 2 轮流进行自己的回合,玩家 1 先手。开始时,两个玩家的初始分值都是 0 。每一回合,玩家从数组的任意一端取一个数字(即,nums[0] 或 nums[nums.length - 1]),取到的数字将会从数组中移除(数组长度减 1 )。玩家选中的数字将会加到他的得分上。当数组中没有剩余数字可取时,游戏结束。
如果玩家 1 能成为赢家,返回 true 。如果两个玩家得分相等,同样认为玩家 1 是游戏的赢家,也返回 true 。你可以假设每个玩家的玩法都会使他的分数最大化。
示例 1:
输入: nums = [1,5,2]
输出: false
**解释:**一开始,玩家 1 可以从 1 和 2 中进行选择。
如果他选择 2(或者 1 ),那么玩家 2 可以从 1(或者 2 )和 5 中进行选择。如果玩家 2 选择了 5 ,那么玩家 1 则只剩下 1(或者 2 )可选。
所以,玩家 1 的最终分数为 1 + 2 = 3,而玩家 2 为 5 。
因此,玩家 1 永远不会成为赢家,返回 false 。
示例 2:
输入: nums = [1,5,233,7]
输出: true
解释: 玩家 1 一开始选择 1 。然后玩家 2 必须从 5 和 7 中进行选择。无论玩家 2 选择了哪个,玩家 1 都可以选择 233 。
最终,玩家 1(234 分)比玩家 2(12 分)获得更多的分数,所以返回 true,表示玩家 1 可以成为赢家。
提示:
- 1 <= nums.length <= 20
- 0 <= nums[i] <= 107
思路
1、递归函数
- 每次玩家只能取最左端或者最右端,这里只统计先手玩家的得分,取得数字则加,对手取得数字则减
- 这就可以化为一个典型的递归问题,先手玩家每次只取最优解,即可得到最终的结果
2、动态规划
- 使用递归函数会造成大量的步骤重复,数据量大时容易超时
- 可以使用动态规划,使用一个二维dp数组
- dp[i][j]表示剩余的整数的下标i<=x<=j,当i==j时表示只剩下一个整数待取
- 每次取下标i或者下标j的整数来得分,所以要在这两种情况下取最优解
- dp[i][j] = max((nums[i]-dp[i+1][j]),(nums[j]-dp[i][j-1]))
#递归函数
class Solution(object):
def PredictTheWinner(self, nums):
def total(start,end,turn):
if start == end:
return nums[start]*turn
scoreStart = nums[start]*turn + total(start+1,end,turn*-1)
scoreEnd = nums[end]*turn + total(start, end-1,turn*-1)
if turn == 1:
return max(scoreEnd,scoreStart)
else:
return min(scoreEnd,scoreStart)
return total(0,len(nums)-1,1) >= 0
#动态规划
class Solution(object):
def PredictTheWinner(self, nums):
n = len(nums)
dp = [[0 for i in range(n)] for i in range(n)]
for i in range(n):
dp[i][i] = nums[i]
for i in range(n-2,-1,-1):
for j in range(i+1,n):
dp[i][j] = max((nums[i]-dp[i+1][j]),(nums[j]-dp[i][j-1]))
return dp[0][n-1]>=0
边栏推荐
猜你喜欢

15_ Redis_ Redis. Conf detailed explanation

Leetcode skimming -- count the number of numbers with different numbers 357 medium

党史纪实主题公益数字文创产品正式上线

2022 年辽宁省大学生数学建模A、B、C题(相关论文及模型程序代码网盘下载)
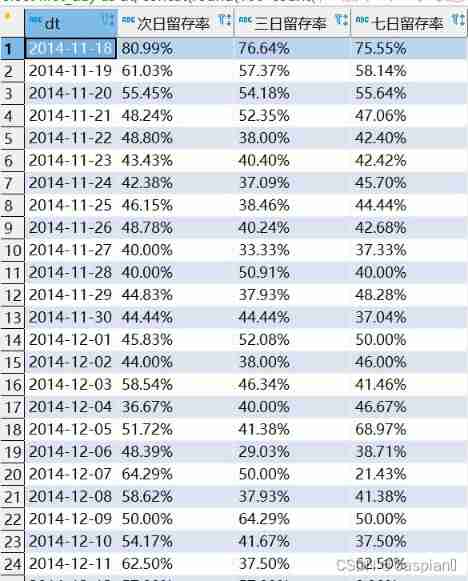
MySQL calculate n-day retention rate

4. Jctree related knowledge learning

6.12 企业内部upp平台(Unified Process Platform)的关键一刻
XML配置文件
. Solution to the problem of Chinese garbled code when net core reads files
Steps for Navicat to create a new database
随机推荐
LeetCode刷题——递增的三元子序列#334#Medium
彻底弄懂浏览器强缓存和协商缓存
夏季高考文化成绩一分一段表
Guangzhou Emergency Management Bureau issued a high temperature and high humidity chemical safety reminder in July
vChain: Enabling Verifiable Boolean Range Queries over Blockchain Databases(sigmod‘2019)
03. Preliminary use of golang
07_哈希
Facing the challenge of "lack of core", how can Feiling provide a stable and strong guarantee for customers' production capacity?
4. Data splitting of Flink real-time project
数据分析常见的英文缩写(一)
folium地图无法显示的问题,临时性解决方案如下
做好抗“疫”之路的把关人——基于RK3568的红外热成像体温检测系统
终于搞懂了JS中的事件循环,同步/异步,微任务/宏任务,运行机制(附笔试题)
04.进入云原生后的企业级应用构建的一些思考
16_Redis_Redis持久化
Common English abbreviations for data analysis (I)
FPGA - 7系列 FPGA内部结构之Clocking -03- 时钟管理模块(CMT)
03_线性表_链表
YOLOV5 代码复现以及搭载服务器运行
Case introduction and problem analysis of microservice