当前位置:网站首页>[cf gym101196-i] waif until dark network maximum flow
[cf gym101196-i] waif until dark network maximum flow
2022-07-06 07:31:00 【PushyTao】
Topic link 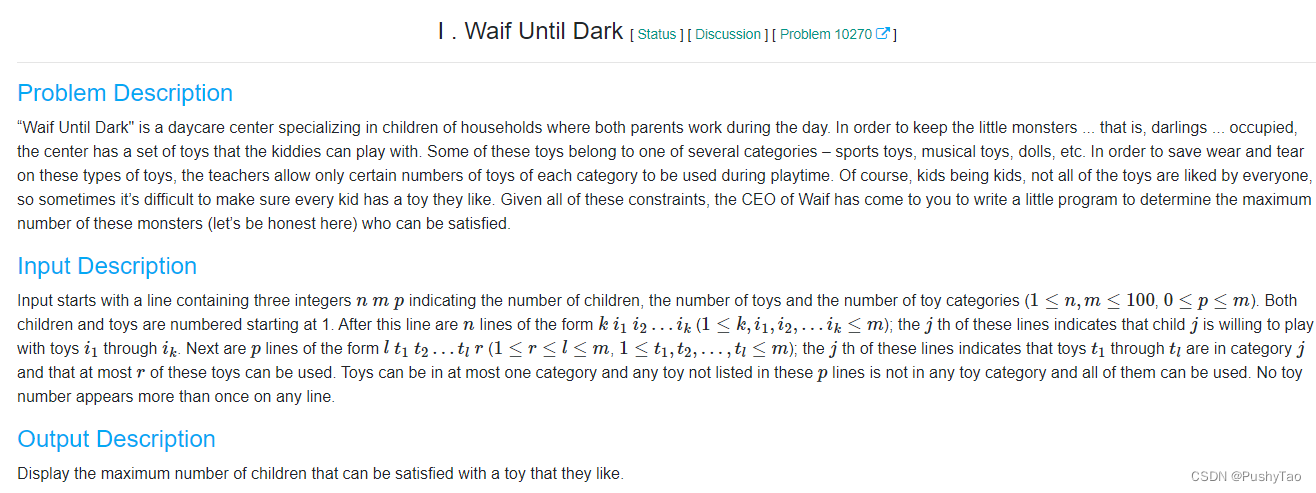
Input
4 3 1
2 1 2
2 1 2
1 3
1 3
2 1 2 1
Output
2
The main idea of the topic :
Children want to play with toys , Some toys belong to certain categories
But children can only play with some toys of every kind , And children don't like all toys , Every child has his own favorite toys , Ask how many children can be satisfied at most
Input n Represents the number of small flowers ,m Number of toys ,p Number of toy types
And then there was n That's ok {
Here n OK, No i In line :
Each row of a k, And then there was k Number , On behalf of the i Children like to play k The number of toys
}
And then there was p That's ok {
Here p OK, No i In line :
Each line has one l, And then there was l Number , And finally r On behalf of this l Toys belong to the category i, And this kind is most used r individual ( Children can only play with some toys of every kind )
}
And the most important sentence :
Toys can be in at most one category and any toy not listed in these p lines is not in any toy category and all of them can be used. No toy number appears more than once on any line.
Toys belong to one category at most , If some toys are not classified into any category , Can be played at will . And ensure that all toys appear only once in a row
The next step is to build the map :
Determine the source and sink points as 1001、1002
Children want to play with toys =》 Build a capacity of 1 The edge of
Toys belong to { Types of toys } =》 The suggested capacity of toys and types is 1 The edge of ( Note the statistics of toys not added to the category , You can play whatever you like )
Build a capacity of r The edge of ( The types are used at most r individual ( Children can only play with some toys of every kind ))
Build a capacity of 1 The edge of
Finally, connect the child with the meeting point 1002 Connected to a , Establish a capacity of 1 The edge of
Finally get the source point 1001 And meeting point 1002 The maximum flow of can get the maximum number of children that can be satisfied
EK_code:
struct Edge {
int u, v;
ll cap, flow;
Edge(int uu, int vv, ll _cap, ll _flow) {
u = uu, v = vv, cap = _cap, flow = _flow;
}
};
struct EdmondsKarp {
ll n, m;
vector<Edge> edges;
vector<int> G[maxn];
ll a[maxn], p[maxn];
void _init(int n) {
for (int i = 0; i <= n; i++) G[i].clear();
edges.clear();
}
void add(int u, int v, ll cap) {
edges.push_back(Edge(u, v, cap, 0));
edges.push_back(Edge(v, u, 0, 0));
m = edges.size();
G[u].push_back(m - 2);
G[v].push_back(m - 1);
}
ll maxFlow(int s, int t) {
ll Flow = 0;
while (true) {
memset(a, 0, sizeof a);
queue<int> que;
que.push(s);
a[s] = INF;
while (que.size()) {
int u = que.front();
que.pop();
for (int i = 0; i < G[u].size(); i++) {
int id = G[u][i];
Edge &e = edges[id];/// No addition & It's OK, too
int to = e.v;
if (!a[to] && e.cap > e.flow) {
p[to] = id;
a[to] = min(a[u], e.cap - e.flow);
que.push(to);
}
}
if (a[t]) break;
}
if (!a[t]) break;
for (int u = t; u != s; u = edges[p[u]].u) {
edges[p[u]].flow += a[t];
edges[p[u] ^ 1].flow -= a[t];
}
Flow += a[t];
}
return Flow;
}
} slove;
int n, m, s, t;
int mp[maxn];
int main() {
/** cin >> n >> m >> s >> t; slove.init(n); slove.n = n; for (int i = 1; i <= m; i++) { int u = read, v = read; ll cap = read; slove.add(u,v,cap); } cout << slove.maxFlow(s,t) <<endl; **/
int p;
n = read,m = read,p = read;
// n child m toy p cate
slove._init(1007);
for(int i=1; i<=n; i++) {
int cnt = read;
for(int j=1; j<=cnt; j++) {
int u = read;// toy id
slove.add(u,m+i,1);// child <-> toy cap = 1 ok
}
}
for(int i=1; i<=n; i++) {
slove.add(i+m, 1002, 1);// child <-> end cap = 1; ok
}
for(int i=1; i<=p; i++) {
int l = read;
for(int j=1; j<=l; j++) {
int v = read;
mp[v] = 1;
slove.add(m+n+i,v,1);// cate <-> toy cap = 1; ok
}
int amount = read;// r
slove.add(1001,n+m+i,amount);// 1001 <->cate cap = amount; ok
}
for(int i=1; i<=m; i++) {
if(mp[i] == 0) {
slove.add(1001,i,1);// 1001 <-> toy cap = 1;
}
}
int ans = slove.maxFlow(1001,1002);
cout << ans << endl;
return 0;
}
/** 4 3 1 2 1 2 2 1 2 1 3 1 3 2 1 2 1 **/
Dinic_code:
struct Edge {
int u, v;
ll cap, flow;
Edge(int _u, int _v, ll _cap, ll _flow) {
u = _u, v = _v;
cap = _cap, flow = _flow;
}
};
struct Dinic {
vector<Edge> edge;
vector<int> G[maxn];
ll dis[maxn],cur[maxn];
int n,s,t;
bool vis[maxn];
void init(int x,int _s,int _t){
n = x;
for(int i = 0;i <= n;i++) G[i].clear();
s = _s,t = _t;
edge.clear();
}
void add(int u,int v,ll cap){
edge.push_back(Edge(u,v,cap,0));
edge.push_back(Edge(v,u,0,0));
G[u].push_back(edge.size() - 2);
G[v].push_back(edge.size() - 1);
}
bool bfs(int s,int t){
queue<int> que;
memset(vis,0,sizeof vis);
// memset(dis,0,sizeof dis);
dis[s] = 0;
que.push(s);
vis[s] = 1;
while(que.size()){
int u = que.front();
que.pop();
for(int i=0;i<G[u].size();i++){
int id = G[u][i];
int to = edge[id].v;
if(!vis[to] && edge[id].cap > edge[id].flow){
dis[to] = dis[u] + 1;
que.push(to);
vis[to] = 1;
}
}
}
return vis[t];
}
ll dfs(int s,int t,ll rest){
if(s == t || rest == 0) return rest;
ll sum = 0LL;
ll Flow = 0, f;
for(ll& i = cur[s];i < G[s].size();i ++){
Edge& e = edge[G[s][i]];
if(dis[s] + 1 == dis[e.v] && (f = dfs(e.v ,t,min(rest,e.cap - e.flow))) > 0){
e.flow += f;
edge[G[s][i] ^ 1].flow -= f;
Flow += f;
rest -= f;
if(rest == 0) break;
}
}
return Flow;
}
ll getMaxFlow(int s,int t){
ll ans = 0;
while(bfs(s,t)) {
memset(cur,0,sizeof cur);
ans += dfs(s,t,0x3f3f3f3f);
}
return ans;
}
} solve;
int mp[1007];
int main() {
int n = read,m = read,p = read;
solve.init(1000,1001,1002);
for(int i=1; i<=n; i++) {
int cnt = read;
for(int j=1; j<=cnt; j++) {
int u = read;// toy id
solve.add(u,m+i,1);// child <-> toy cap = 1 ok
}
}
for(int i=1; i<=n; i++) {
solve.add(i+m, 1002, 1);// child <-> end cap = 1; ok
}
for(int i=1; i<=p; i++) {
int l = read;
for(int j=1; j<=l; j++) {
int v = read;
mp[v] = 1;
solve.add(m+n+i,v,1);// cate <-> toy cap = 1; ok
}
int amount = read;// r
solve.add(1001,n+m+i,amount);// 1001 <-> cate cap = amount; ok
}
for(int i=1; i<=m; i++) {
if(mp[i] == 0) {
solve.add(1001,i,1);// 1001 <-> toy cap = 1;
}
}
int ans = solve.getMaxFlow(1001,1002);
cout << ans << endl;
return 0;
}
/** **/
边栏推荐
- Supervisor usage document
- word中如何删除某符号前面或后面所有的文字
- Brief explanation of instagram operation tips in 2022
- Set picture annotation in markdown
- 杰理之蓝牙设备想要发送数据给手机,需要手机先打开 notify 通道【篇】
- word设置目录
- Three no resumes in the software testing industry. What does the enterprise use to recruit you? Shichendahai's resume
- qt颜色与字符串、uint相互转换
- Ble of Jerry [chapter]
- C # display the list control, select the file to obtain the file path and filter the file extension, and RichTextBox displays the data
猜你喜欢

Go learning -- implementing generics based on reflection and empty interfaces
![[MySQL learning notes 32] mvcc](/img/0d/2df82b63d1eb3283a84e27f67c1523.png)
[MySQL learning notes 32] mvcc

The way to learn go (I) the basic introduction of go to the first HelloWorld

TypeScript接口与泛型的使用
数字IC设计笔试题汇总(一)

The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
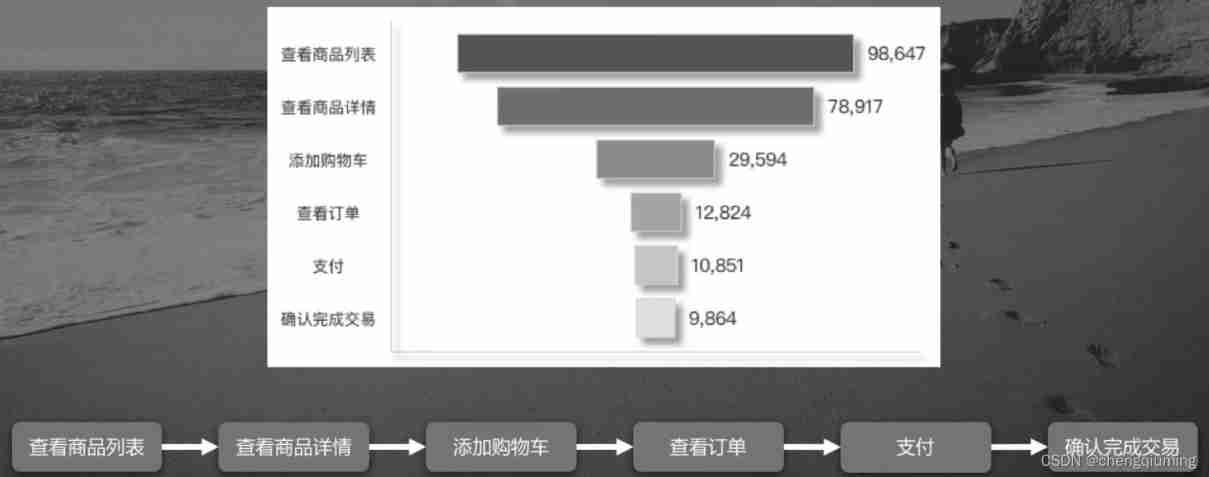
Path analysis model
SSM learning
![Jerry's ad series MIDI function description [chapter]](/img/28/e0f9b41db597ff3288af431c677001.png)
Jerry's ad series MIDI function description [chapter]

Lesson 12 study notes 2022.02.11
随机推荐
Relevant introduction of clip image
[CF Gym101196-I] Waif Until Dark 网络最大流
The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
Mise en œuvre du langage leecode - C - 15. Somme des trois chiffres - - - - - idées à améliorer
CF1036C Classy Numbers 题解
[MySQL learning notes 30] lock (non tutorial)
Sélectionnez toutes les lignes avec un symbole dans Word et changez - les en titre
Oracle column to row -- a field is converted to multiple rows according to the specified separator
[dictionary tree] [trie] p3879 [tjoi2010] reading comprehension
剪映的相关介绍
Crawling exercise: Notice of crawling Henan Agricultural University
JMeter performance test steps practical tutorial
杰理之开发板上电开机,就可以手机打开 NRF 的 APP【篇】
Simulation of Michelson interferometer based on MATLAB
Jerry's general penetration test - do data transmission with app Communication [article]
TypeScript接口与泛型的使用
Méthode d'obtention des propriétés de l'objet JS (.Et [] méthodes)
word怎么只删除英语保留汉语或删除汉语保留英文
【MySQL学习笔记32】mvcc
QT color is converted to string and uint