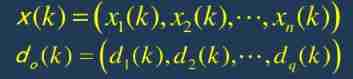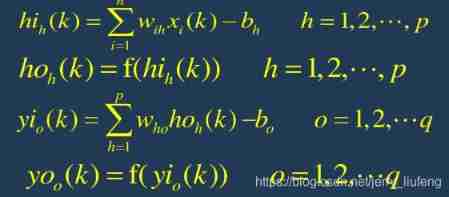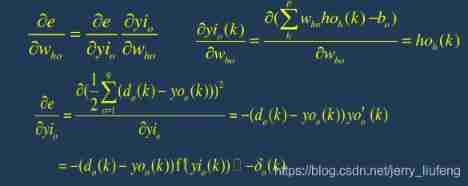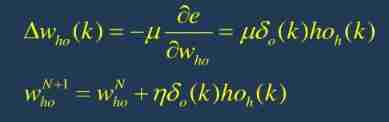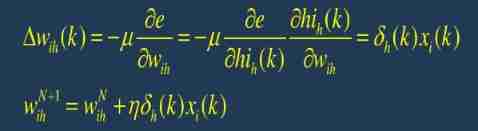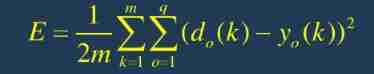Machine learning -- neural network (IV): BP neural network

BP neural network （Back Propagation）

   Error back propagation algorithm （error Back Propagation abbreviation BP）, It is actually a kind of multilayer perceptron , stay 1986 from Rumelhart and Hinton The scientific group headed by .BP Neural network has the ability of arbitrarily complex pattern classification and excellent multi-dimensional function mapping , It solves the XOR problem and other problems that simple perceptron cannot solve . In terms of structure, it has an input layer 、 The hidden layer and the output layer ; In essence, it takes the square of network error as the objective function 、 The gradient descent method is used to calculate the minimum value of the objective function .

BP Neural network structure

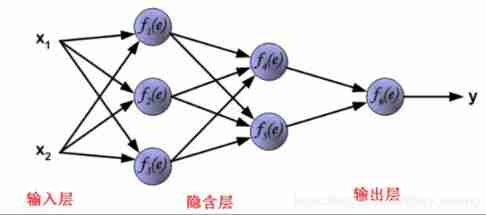
1. The main process

• (1) A sub process in which the working signal propagates forward
• (2) The sub process of error signal back propagation and back feedback
  To borrow an example BP（Back Propagation） Neural network learning notes ： I want to pursue the goddess , Then I have to show it ！ So I bought her flowers , Please her . then , She gave me some indication （ Or hint ）, According to this expression , Compare it with my ultimate goal （ Pursue the goddess ）, Then I make adjustments and continue to say , It's been going back and forth , Until the ultimate goal is achieved —— Success seeks the goddess most . My expression is “ The signal travels forward ”, The expression of the goddess is “ Error back propagation ”. This is it. BP The core of neural network .

• The main process is ：
  Forward propagation results in output

BP Positive communication

least square 、 Gradient descent and other methods are used to compare labels and outputs , Feed back the result error layer by layer , Update the weights

BP Feedback back propagation

2. The whole idea

• Learning goals ：

Get a model , When inputting a new set of data, we can output the data we expect

• Learning style ：

The input sample data is processed by the activation function to get the output , Output compared with known tags , Change the weight in reverse .

• The essence of learning ：

Dynamically adjust various connection weights

• The core of learning ：

Adjustment of weight （ Certain adjustment rules for the connection rights of each neuron in the learning process ）

3. Algorithm details

   Neural networks simulate biological neural structures and activities , Construction of classifier . The basic unit of composition is neurons , When the parameter of input neuron is greater than a certain threshold , Neurons become excited , To produce output , Otherwise no response . This input is related to all the neurons connected to it , The response function of neurons can be divided into many different forms （ The activation function ）.
So let's talk about that ：

1. Activation function
2. BP deduction

1） Activation function

Definition ： Each neuron node in the neural network accepts The output value of the upper layer neuron is used as the input value of this neuron , And pass the input value to the next layer , The input layer neuron node will pass the input attribute values directly to the next layer （ Hidden layer or output layer ）. In multilayer neural networks , There is a functional relationship between the output of the upper node and the input of the lower node , This function is called the activation function （ It's also called the excitation function ）.

Application reason ： Don't use activation function ($f(x)=x$), The input of each layer node is a linear function of the output of the upper layer , No matter how many hidden layers , The final output is a linear combination of inputs , Equivalent to the most primitive perceptron , The approximation ability of the network is very limited .

Common activation functions and their characteristics ：

（1）sigmoid function
Nonlinear activation function , The mathematical formula is ：
$$f(z)=\frac{1}{1+e^{-z}}$$
The geometric image is ：

sigmoid Function and its derivative image

characteristic ：

The continuous value entered can be converted into 0 and 1 Between the output , If it is a very small negative number, the output is 0, Very large positive numbers are output as 1

shortcoming ：

• Gradient explosion and gradient disappearance are caused by gradient back propagation in deep neural network
• sigmoid Output output No 0 mean value （zero-centerd）
• The analytic expression contains power operation , The cost of calculation is high , For large-scale machine learning algorithm and training process, the consumption of time and space is high

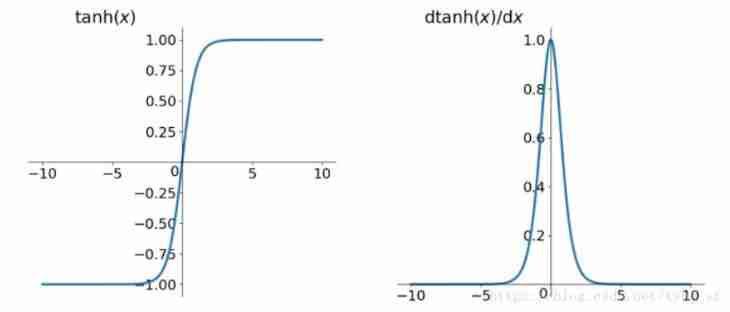
（2）tanh function
Function analytic formula ：
$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
tanh Function and its derivative image

tanh Function and its derivative image

advantage ：

• It's solved Sigmoid The function is not zero-centered Output problem

Insufficient ：

• The problems of gradient vanishing and power operation still exist

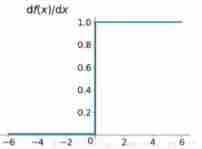
（3）Relu function
Relu Function analytic formula
$$Relu=max(0,x)$$
Relu Function and its derivative image

Relu Function and its derivative image

describe >Relus Is a function that takes the maximum value , Functions are not derivable across regions

advantage

• Solved the gradient disappear （gradient vanishing） The problem of （ In the positive range ）
• Does not contain power exponent calculation , Fast calculation
• The convergence rate is faster

Pay attention to problems ：

• Relu The output of is not zero-centered Value
• Deep ReLU Problem, That is, some neurons may never be activated , As a result, the corresponding parameters will never be updated （ Main cause ：
  （1）： The initialization parameters are poor , It's very unlikely to happen ;
  （2）learning rate Too high ）

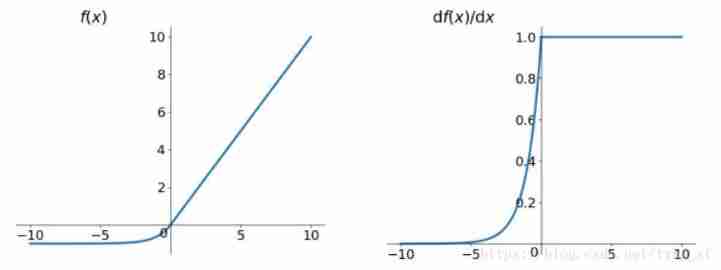
（4）Leaky ReLU function （ At present, the most widely used and general activation function）
Function expression ：
$$f(x)=max(ax,x)$$
Leaky ReLU Images of functions and their derivatives ：

Leakey Relu Function image

Leakey Relu Function derivative image

explain ：

In order to solve Dead ReLU Problem, Put forward the idea of ReLU The first half of becomes not 0 Of ax, Usually a=0.01
look Leaky ReLU have ReLU The advantages of , And to a certain extent, it overcomes ReLU The shortcomings of , But in fact, it is usually used ReLU, There is no complete proof Leaky ReLU Always better than ReLU

（5）ELU（exponential Linear Units） function
Function expression ：
$$f(x)=\{\begin{array}{rcl}x& & ifx>0\\ a（e^x-1)）& & otherwise\end{array}$$
Images of functions and their derivatives

ELU Functions and their derivatives

advantage ： >* non-existent Dead ReLU Problem >* The average value of the output is close to 0,zero-centered

A small problem ：

The calculation is a little bit more

2） BP deduction

Defining variables :

Derivation process ：

1. Network initialization ：
The main thing is to initialize the connection weights w, The range of values is （-1,1）; Set the error function e; Given the calculation accuracy value $ϵ$ And the maximum number of studies M.

2. Randomly select the second k Input samples and their corresponding expected outputs （ Label results ）

3. Calculate the input and output of each neuron in the hidden layer

4. Using the expected output and the actual output of the network , Calculate the error function e Partial derivatives of neurons in the output layer

5. Use the connection weight from hidden layer to output layer 、 Output value of hidden layer 、 The partial derivative of the output layer calculates the partial derivative of the error function to each neuron of the hidden layer

6. According to the output layer of each neuron ${\delta }_o(k)$ And the output of each neuron in the hidden layer to modify the connection weight $w_{ho}(k)$

7. Using the ${\delta }_o(k)$ Connection right with the output layer of the input layer

8. Calculate global error ：

9. Judge whether the error or iteration times meet the requirements , When the error is within a certain accuracy range or reaches the number of iterations, the cycle ends . Otherwise, return to step 3 and repeat the next round of learning .

4. Code implementation

import math
import random
import numpy as np
import matplotlib.pyplot as plt
random.seed(0)  # random Add seeds , Let the random number generated each time be the same 
def rand(a, b):
    ''' Random function '''
    return (b - a) * random.random() + a


def make_matrix(m, n, fill=0.0):
    #  Method 1,： Use it directly numpy Of zeros function 
    return np.zeros([m,n]).tolist()

    # Method 2： Definition list, Join line by line 
    # mat = []
    # for i in range(m):
    # mat.append([fill] * n)
    # return mat

def sigmoid(x):
    '''sigmoid Activation function '''
    return 1.0 / (1.0 + math.exp(-x))


def sigmoid_derivative(x):
    '''sigmoid Derivative of a function '''
    return x * (1 - x)


class BPNeuralNetwork:
    def __init__(self):
        self.input_n = 0           #  Initialize the number of neurons in the input layer 
        self.hidden_n = 0          #  Initialize the number of hidden layer neurons 
        self.output_n = 0          #  Initialize the number of neurons in the output layer 
        self.input_cells = []      #  Initialize input layer neurons 
        self.hidden_cells = []     #  Initialize hidden layer neurons 
        self.output_cells = []     #  Initialize output layer neurons 
        self.input_weights = []    #  Input layer to hidden layer weight 
        self.output_weights = []   #  Weight from hidden layer to output layer 
        self.input_correction = [] #  Input layer correction value 
        self.output_correction = [] #  Correction value of output layer 

    def setup(self, ni, nh, no):
        ''' ni—— The number of neurons in the input layer  nh—— Number of hidden layer neurons  no—— The number of neurons in the output layer  '''
        self.input_n = ni + 1      # Add a column of offset values 
        self.hidden_n = nh
        self.output_n = no
        # init cells
        self.input_cells = [1.0] * self.input_n   #  initialization 1 That's ok ni+1 The unit matrix of the column 
        self.hidden_cells = [1.0] * self.hidden_n #  initialization 1 That's ok nh The unit matrix of the column 
        self.output_cells = [1.0] * self.output_n #  initialization 1 That's ok no The unit matrix of the column 
        #  Initialize the weight between the input layer and the hidden layer 
        self.input_weights =(np.random.random([self.input_n,self.hidden_n])-0.8)
        #  Initialize the weight between the input layer and the hidden layer 
        self.output_weights =(np.random.random([self.hidden_n,self.output_n]))*2 
        #  Initialize the correction matrix 
        self.input_correction = make_matrix(self.input_n, self.hidden_n)
        self.output_correction = make_matrix(self.hidden_n, self.output_n)

    def predict(self, inputs):
        #  Activate output layer neurons 
        for i in range(self.input_n - 1):
            self.input_cells[i] = inputs[i]
        #  Activate hidden layer neurons 
        for j in range(self.hidden_n):
            total = 0.0
            for i in range(self.input_n):
                total += self.input_cells[i] * self.input_weights[i][j]
            self.hidden_cells[j] = sigmoid(total)
        #  Activate output layer neurons （ That is, the output result ）
        for k in range(self.output_n):
            total = 0.0
            for j in range(self.hidden_n):
                total += self.hidden_cells[j] * self.output_weights[j][k]
            self.output_cells[k] = sigmoid(total)
        return self.output_cells[:]

    def back_propagate(self, case, label, learn, correct):
        ''' case—— input data  label—— Tag data  learn—— Learning rate  correct—— Correction parameters  '''
        #  Forward pass parameter 
        self.predict(case)
        #  Obtain the output layer error and the partial derivative of the error relative to the output layer neuron 
        output_deltas = [0.0] * self.output_n
        for o in range(self.output_n):
            error = label[o] - self.output_cells[o]
            output_deltas[o] = sigmoid_derivative(self.output_cells[o]) * error
        #  Obtain the relative error of the hidden layer and its partial derivative relative to the hidden layer neuron 
        hidden_deltas = [0.0] * self.hidden_n
        for h in range(self.hidden_n):
            error = 0.0
            for o in range(self.output_n):
                error += output_deltas[o] * self.output_weights[h][o]
            hidden_deltas[h] = sigmoid_derivative(self.hidden_cells[h]) * error
        #  Update the weight from the hidden layer to the output layer 
        for h in range(self.hidden_n):
            for o in range(self.output_n):
                change = output_deltas[o] * self.hidden_cells[h]
                self.output_weights[h][o] += learn * change + correct * self.output_correction[h][o]
                self.output_correction[h][o] = change
        #  Update the weight from input layer to output layer 
        for i in range(self.input_n):
            for h in range(self.hidden_n):
                change = hidden_deltas[h] * self.input_cells[i]
                self.input_weights[i][h] += learn * change + correct * self.input_correction[i][h]
                self.input_correction[i][h] = change
        #  Get global error 
        error = 0.0
        for o in range(len(label)):
            error += 0.5 * (label[o] - self.output_cells[o]) ** 2
        return error

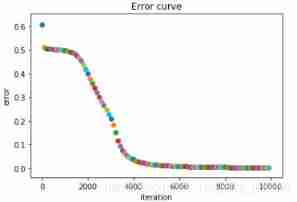
    def train(self, cases, labels, limit=10000, learn=0.05, correct=0.1):
        for j in range(limit):
            error = 0.0
            for i in range(len(cases)):
                label = labels[i]
                case = cases[i]
                error += self.back_propagate(case, label, learn, correct)
            if j%100==0:   
                plt.scatter(j,error)
        plt.title('Error curve')
        plt.xlabel('iteration')
        plt.ylabel('error')
        plt.show()

    def test(self):
        cases = [
            [0, 0],
            [0, 1],
            [1, 0],
            [1, 1],
        ]
        labels = [[0], [1], [1], [0]]
        self.setup(2, 5, 1)
        self.train(cases, labels, 10000, 0.05, 0.1)
        for case in cases:
            print(self.predict(case))


if __name__ == '__main__':
    nn = BPNeuralNetwork()
    nn.test()

result ：

Output results ：

Error iteration diagram ：

explain ：

In iteration to 1400 The error obviously began to decrease at the second time , Iterate to 4000 The error reduction is not obvious at the second time .（ Different initialization parameters have different reduction efficiency ）

To have come , Point a favor and give a suggestion before you leave