当前位置:网站首页>内部排序——插入排序
内部排序——插入排序
2022-07-07 12:33:00 【InfoQ】
1.插入排序
- 直接插入排序
- 折半插入法
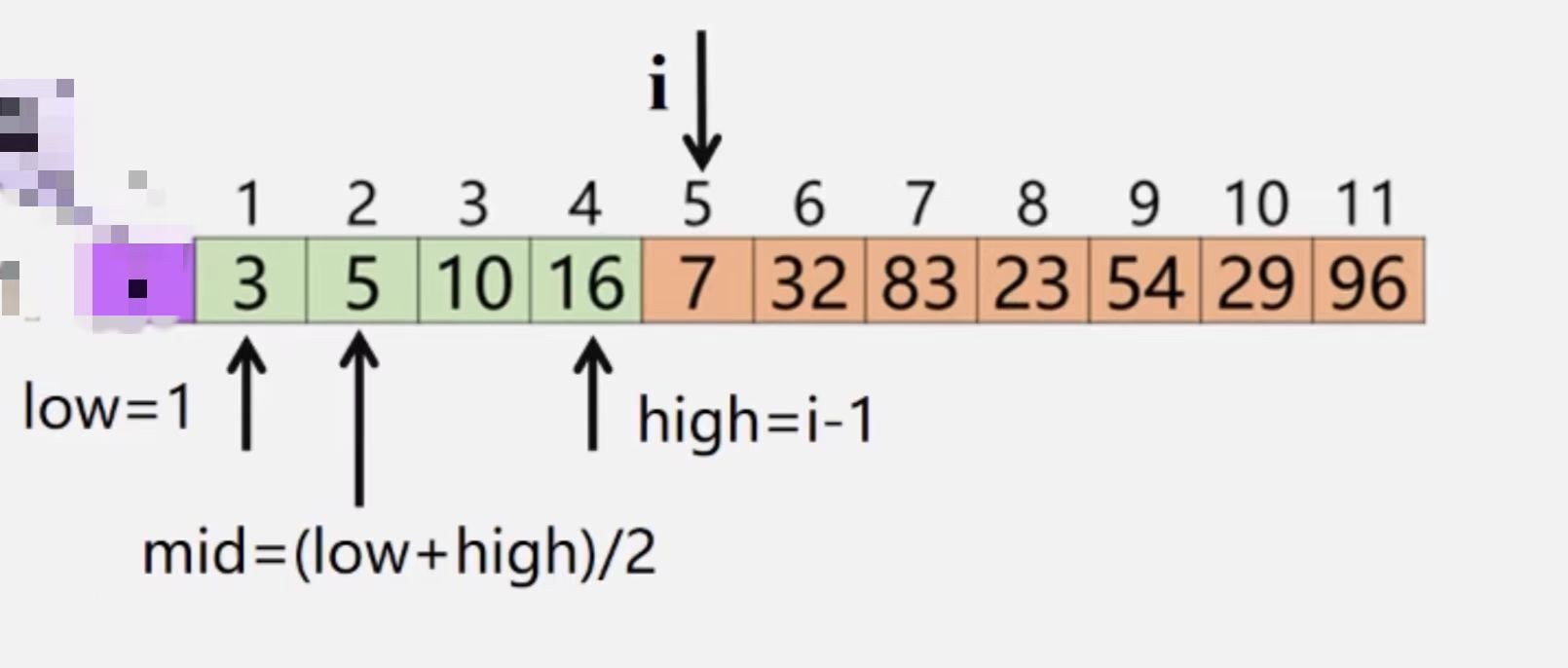
- 2-路插入排序(不是很常用)

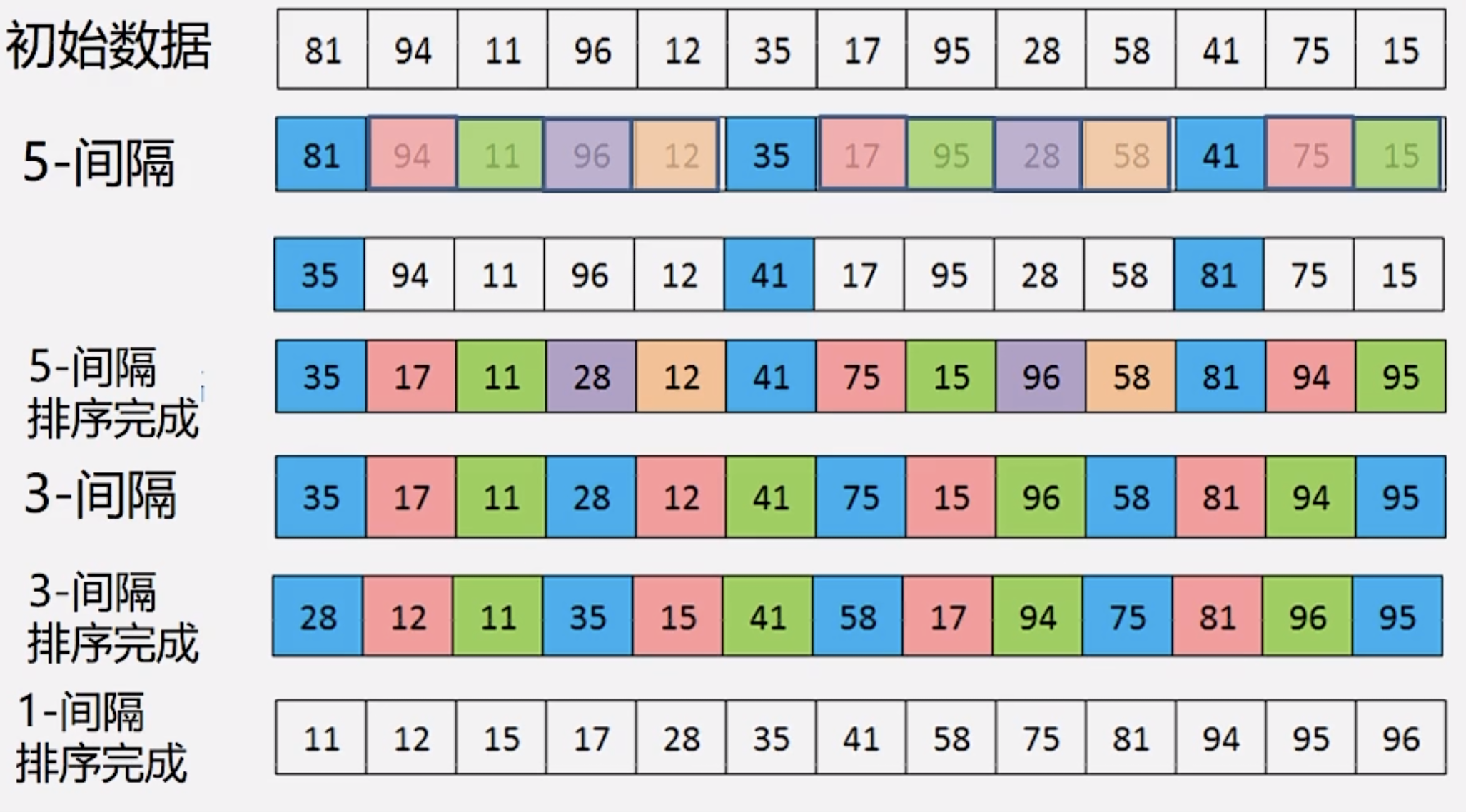
- 希尔排序(重点)
总结
- 直接插入排序当数量很小的时候是一种很好的排序方法,但对于数量过多的不适用。
- 折半插入排序是对直接排序的一种改进,它是在有序子表中查找待排序记录位置,利用折半查找的方式,减少比较时间。
- 2-路插入排序是在折半插入排序的基础上的发展。其目的是减少排序过程中记录移动的次数,但为此需n个记录的辅助空间。
- 希尔排序是对数列进行奇数间隔,被间隔数进行排序。(一定要是奇数)这个方法比较好,但不稳定。注意重点掌握这个方法。
边栏推荐
- Vmware共享主机的有线网络IP地址
- Verilog implementation of a simple legv8 processor [4] [explanation of basic knowledge and module design of single cycle implementation]
- Introduction to sakt method
- Laravel5 call to undefined function OpenSSL cipher IV length() error php7 failed to open OpenSSL extension
- Excerpt from "misogyny: female disgust in Japan"
- 常用數字信號編碼之反向不歸零碼碼、曼徹斯特編碼、差分曼徹斯特編碼
- 请问,在使用flink sql sink数据到kafka的时候出现执行成功,但是kafka里面没有数
- ARM Cortex-A9,MCIMX6U7CVM08AD 处理器应用
- 内存溢出和内存泄漏的区别
- FCOS3D label assignment
猜你喜欢
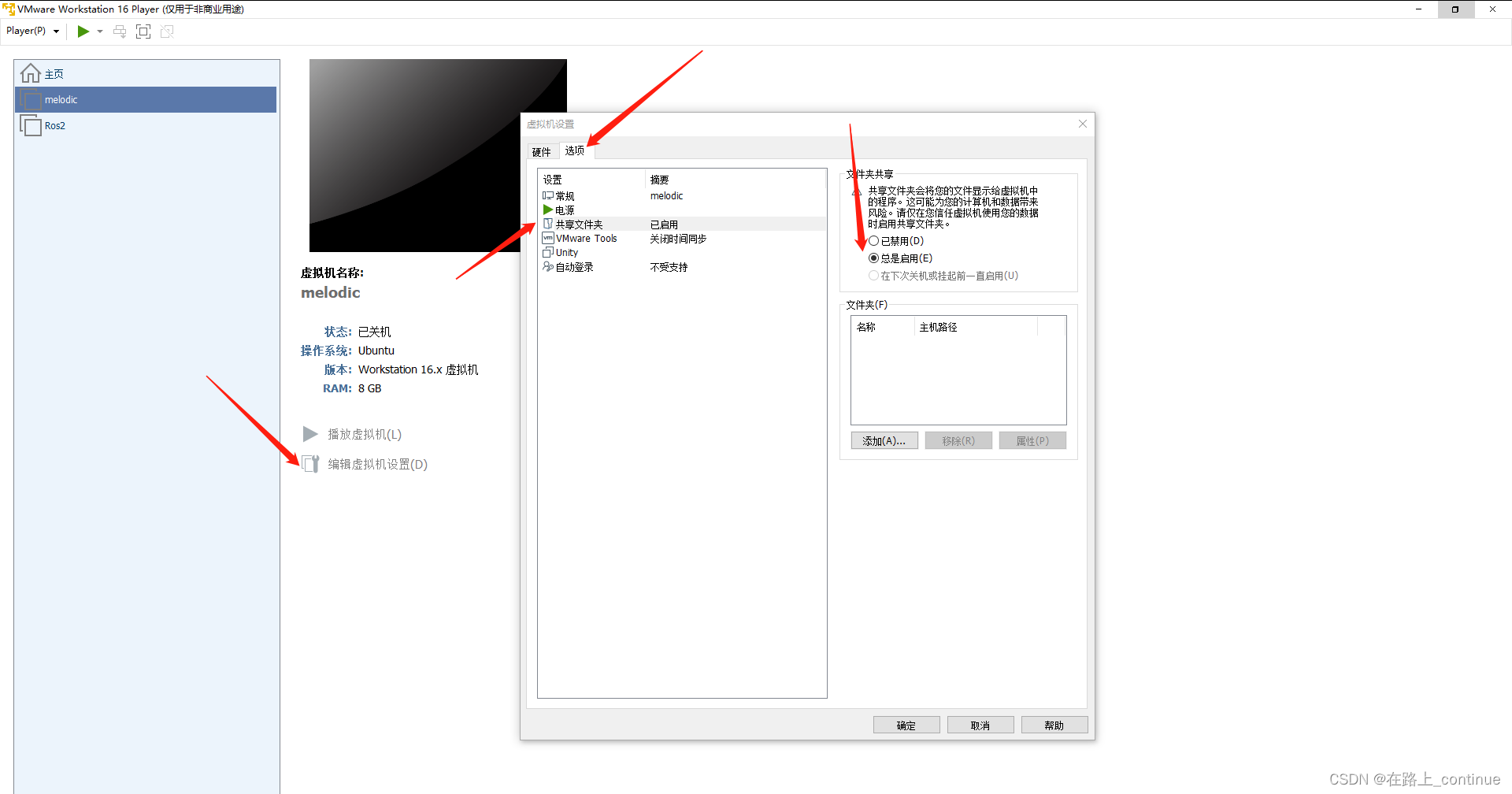
Vmware 与主机之间传输文件
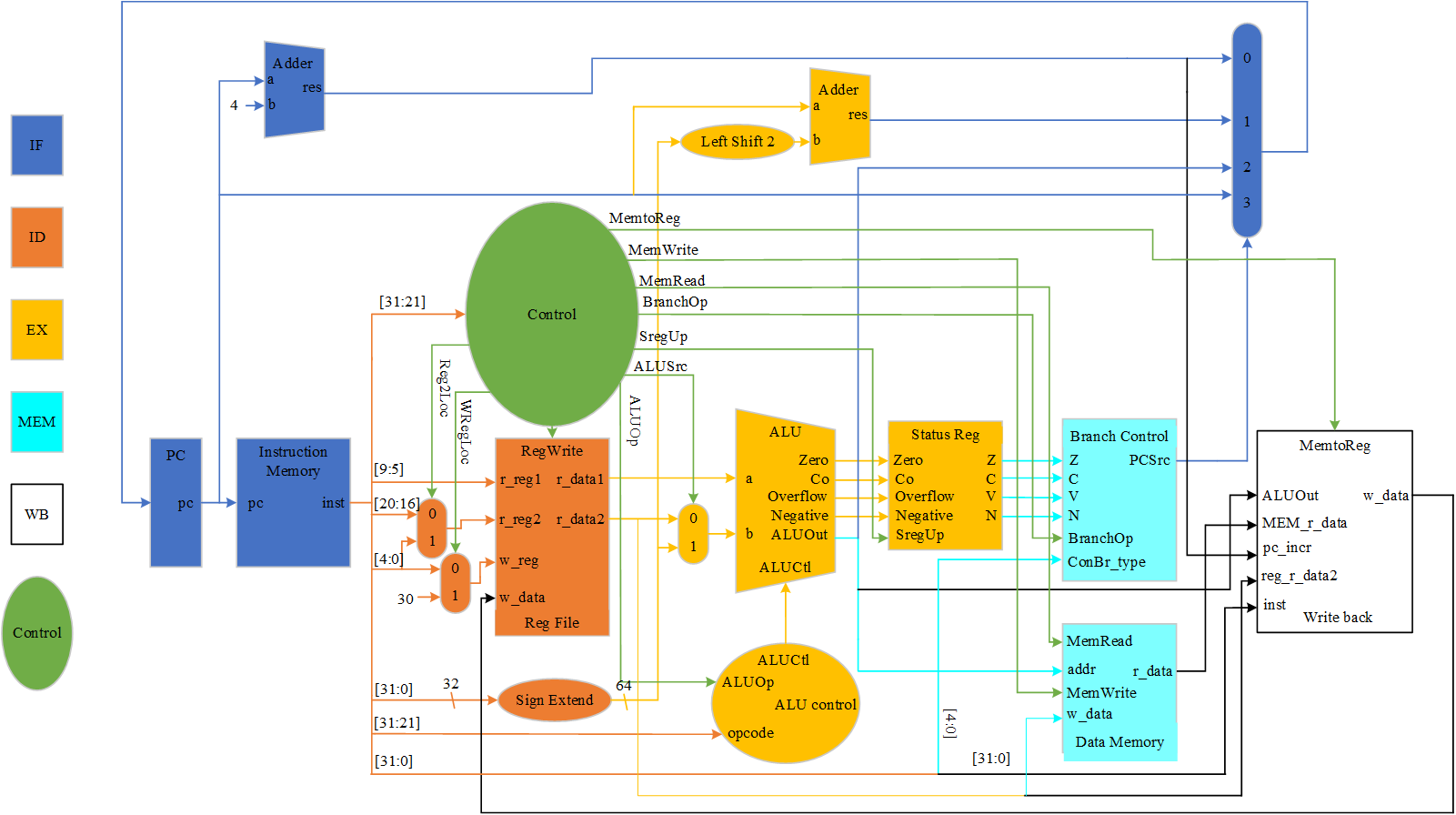
一个简单LEGv8处理器的Verilog实现【四】【单周期实现基础知识及模块设计讲解】

Flask session forged hctf admin
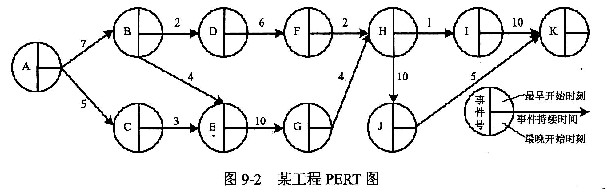
PERT图(工程网络图)

The longest ascending subsequence model acwing 482 Chorus formation
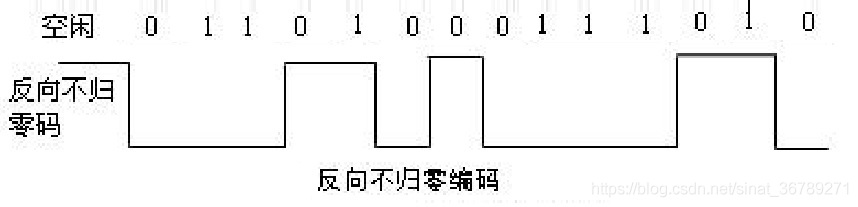
常用数字信号编码之反向不归零码码、曼彻斯特编码、差分曼彻斯特编码

docker部署oracle
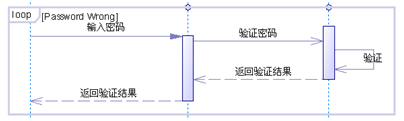
UML sequence diagram (sequence diagram)
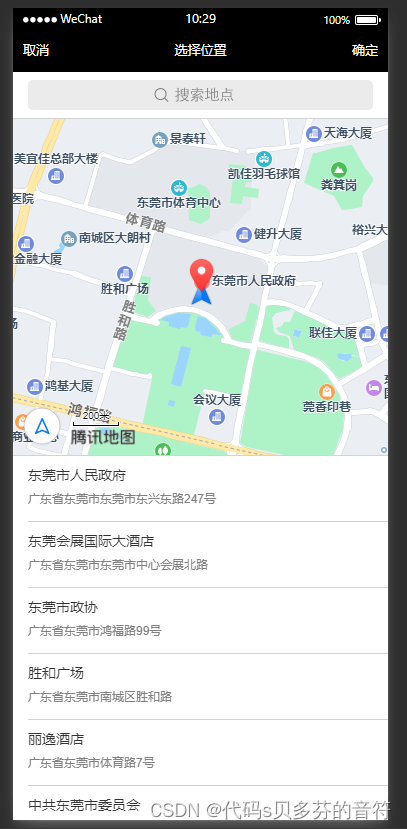
js 获取当前时间 年月日,uniapp定位 小程序打开地图选择地点

UML 顺序图(时序图)
随机推荐
Use day JS let time (displayed as minutes, hours, days, months, and so on)
Million data document access of course design
AI人才培育新思路,这场直播有你关心的
Transferring files between VMware and host
[fortress machine] what is the difference between cloud fortress machine and ordinary fortress machine?
Arm cortex-a9, mcimx6u7cvm08ad processor application
VSCode 配置使用 PyLint 语法检查器
内存溢出和内存泄漏的区别
THINKPHP框架的优秀开源系统推荐
The delivery efficiency is increased by 52 times, and the operation efficiency is increased by 10 times. See the compilation of practical cases of financial cloud native technology (with download)
Pert diagram (engineering network diagram)
CSMA/CD 载波监听多点接入/碰撞检测协议
Leetcode——剑指 Offer 05. 替换空格
Bashrc and profile
用例图
call undefined function openssl_cipher_iv_length
Is it safe to open an account online now? Which securities company should I choose to open an account online?
手里的闲钱是炒股票还是买理财产品好?
FCOS3D label assignment
【AI实战】应用xgboost.XGBRegressor搭建空气质量预测模型(二)