当前位置:网站首页>卷积神经网络CNN
卷积神经网络CNN
2022-08-04 06:07:00 【一枚小可爱c】
为什么用CNN处理图像,而不是用全连接网络?
CNN或 ConvNet)是一种 具有局部连接、权重共享等特性的深层前馈神经网络.
卷积神经网络最早主要是用来处理图像信息,在用全连接前馈网络来处理图像时,会存在以下两个问题:
(1)参数太多:如果输入图像大小为100×100x3(即图像高度为100,宽 度为100以及RGB3个颜色通道),在全连接前馈网络中,第一个隐藏层的每个 神经元到输入层都有100 x 100 x3= 30000个互相独立的连接,每个连接都对 应一个权重参数,随着隐藏层神经元数量的增多,参数的规模也会急剧增加,这 会导致整个神经网络的训练效率非常低,也很容易出现过拟合.
(2)局部不变性特征:自然图像中的物体都具有局部不变性特征,比如尺 度缩放、平移、旋转等操作不影响其语义信息,而全连接前馈网络很难提取这些 局部不变性特征,一般需要进行数据增强来提高性能.
感受野
卷积神经网络是受生物学上感受野机制的启发而提出的,感受野(Receptive Field )机制主要是指听觉、视觉等神经系统中一些神经元的特性,即神经元 只接受其所支配的刺激区域内的信号,在视觉神经系统中,视觉皮层中的神经细 胞的输出依赖于视网膜上的光感受器,视网膜上的光感受器受刺激兴奋时,将神 经冲动信号传到视觉皮层,但不是所有视觉皮层中的神经元都会接受这些信号.一个神经元的感受野是指视网膜上的特定区域,只有这个区域内的刺激才能够 激活该神经元.
一维卷积
一维卷积经常用在信号处理中,用于计算信号的延迟累积.假设一个信号发生器每个时刻 t 产生一个信号 x ,其信息的衰减率为 ,即在k-1个时间步长后,信息为原来的
,即在k-1个时间步长后,信息为原来的 倍,假设
倍,假设  ,
, ,
, ,那么在时刻 t 收到的信号
,那么在时刻 t 收到的信号 为当前时刻产生的信息和以前时刻延迟信息的叠加,即
为当前时刻产生的信息和以前时刻延迟信息的叠加,即
我们把w1,w2, 称为滤波器( Filter)或卷积核。
下图给出了两个滤波器的一维卷积示例,可以看出,两个滤波器分别提取 了输入序列的不同特征,滤波器w = [1/3, 1/3,1/3]可以检测信号序列中的低频这 信息,而滤波器w= [1,-2,1]可以检测信号序列中的高频信息.

二维卷积
卷积也经常用在图像处理中,因为图像为一个二维结构,所以需要将一维卷积进行扩展,给定一个图像 和一个滤波器
和一个滤波器 ,一般U<<M,V<<N,其卷积为
,一般U<<M,V<<N,其卷积为
为了简单起见,这里假设卷积的输出 的下标(i,j)从(U,V)开始.
的下标(i,j)从(U,V)开始.
下图是二维卷积的示例

卷积的变种
步长是指卷积核在滑动时的时间间隔,
零填充是指在输入向量两端进行补零,
(下图中 上面那个是步长为2的卷积示例,下面那个是输入两端各补一个零后的卷积示例)

空洞卷积
对于一个卷积层,如果希望增加输出单元的感受野,一般可以通过三种方式实现:
1)增加卷积核的大小;
2)增加层数,比如两层3x3的卷积可以近似一层 5×5卷积的效果;
3)在卷积之前进行汇聚操作,前两种方式会增加参数数量,而 第三种方式会丢失一些信息.
空洞卷积(Atrous Convolution )是一种不增加参数数量,同时增加输出单元感受野的一种方法,也称为膨胀卷积
空洞卷积通过给卷积插入“空洞”来变相地增加其大小,如果在卷积核的每两个元素之间插入D-1个空洞,卷积核的有效大小为
其中D称为膨胀率。当D=1时卷积核为普通的卷积核。
下图给出了空洞卷积的示例

边栏推荐
- MySQL基础(DDL、DML、DQL)
- Network skills: teach you to install batteries on the router, you can still surf the Internet when the power is cut off!
- 两日总结八
- 窥探晶体世界的奥秘 —— 230种空间群晶体结构模型全在这里
- likeshop外卖点餐系统开源啦100%开源无加密
- Faster - RCNN principle and repetition code
- Gramm Angle field GAF time-series data into the image and applied to the fault diagnosis
- Nacos 原理
- Error EPERM operation not permitted, mkdir ‘Dsoftwarenodejsnode_cache_cacach两种解决办法
- FCN - the originator of semantic segmentation (based on tf-Kersa reproduction code)
猜你喜欢
关于我写的循环遍历
ERROR 2003 (HY000) Can‘t connect to MySQL server on ‘localhost3306‘ (10061)解决办法
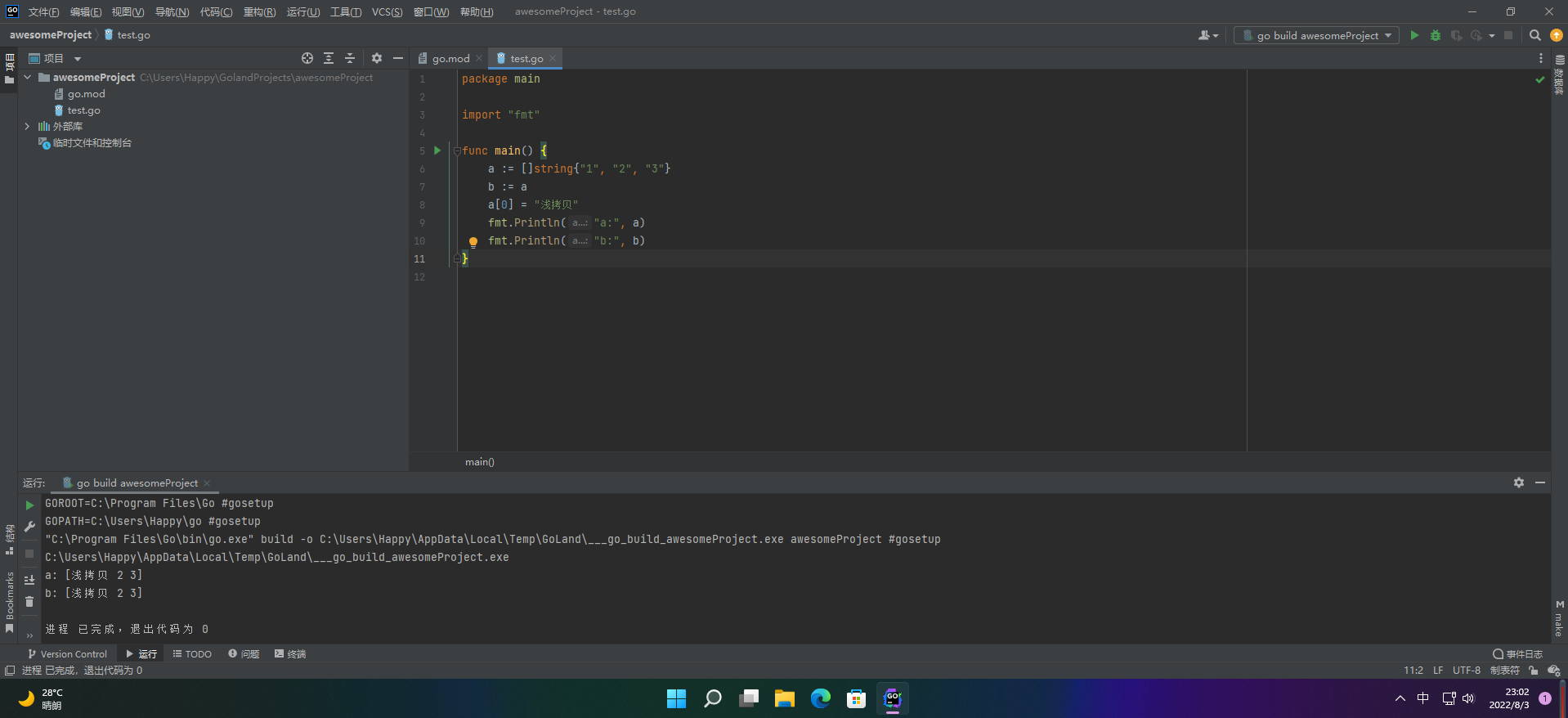
【愚公系列】2022年07月 Go教学课程 027-深拷贝和浅拷贝
Mac安装PHP开发环境
Database knowledge: SQLServer creates non-sa user notes
Software: Recommend a domestic and very easy-to-use efficiency software uTools to everyone
国内外知名源码商城系统盘点
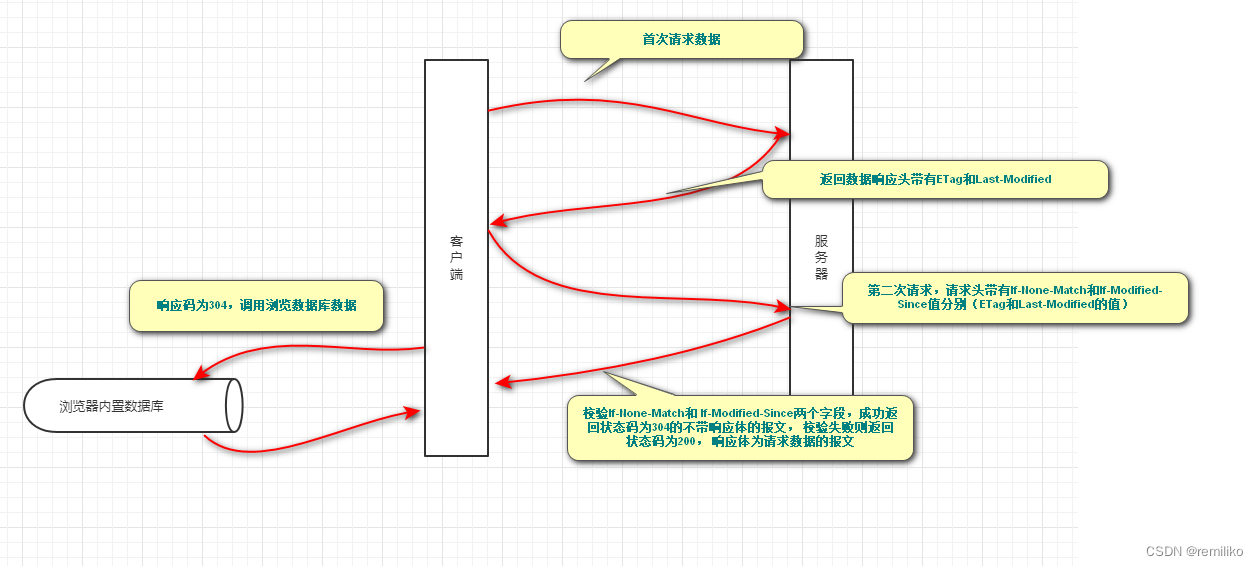
简析强制缓存和协商缓存
Computer software: recommend a disk space analysis tool - WizTree
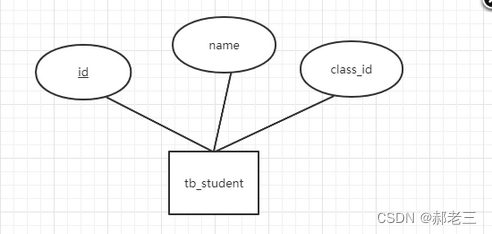
E-R图总结规范
随机推荐
详解CAN总线:常用CAN连接器的使用方法
如何用matlab做高精度计算?【第三辑】(完)
更改mysql数据库默认的字符集(mysql 存储 emoji表情)
电商系统PC商城模块介绍
MySQL复制表结构、表数据的方法
类图规范总结
VMD combined with ISSA to optimize LSSVM power prediction
Time Series Forecasting Based on Reptile Search RSA Optimized LSTM
DropBlock: Regularization method and reproduction code for convolutional layers
【学习笔记】状压dp
【愚公系列】2022年07月 Go教学课程 027-深拷贝和浅拷贝
设置el-table自动向下滑动(不多解释,直接代码实现)
MySQL外键(详解)
零分贝超静音无线鼠标!数量有限!!先到先得!!!【元旦专享】
Amazon亚马逊 Vendor Central Label详解
布隆过滤器
系统流量预估、架构设计方案
两日总结八
FCN - the originator of semantic segmentation (based on tf-Kersa reproduction code)
Database Skills: Organize SQL Server's Very Practical Scripts