当前位置:网站首页>【729. 我的日程安排錶 I】
【729. 我的日程安排錶 I】
2022-07-05 16:49:00 【千北@】
來源:力扣(LeetCode)
描述:
實現一個 MyCalendar 類來存放你的日程安排。如果要添加的日程安排不會造成 重複預訂 ,則可以存儲這個新的日程安排。
當兩個日程安排有一些時間上的交叉時(例如兩個日程安排都在同一時間內),就會產生 重複預訂 。
日程可以用一對整數 start 和 end 錶示,這裏的時間是半開區間,即 [start, end), 實數 x 的範圍為, start <= x < end 。
實現 MyCalendar 類:
- MyCalendar() 初始化日曆對象。
- boolean book(int start, int end) 如果可以將日程安排成功添加到日曆中而不會導致重複預訂,返回 true 。否則,返回 false 並且不要將該日程安排添加到日曆中。
示例:
輸入:
["MyCalendar", "book", "book", "book"]
[[], [10, 20], [15, 25], [20, 30]]
輸出:
[null, true, false, true]
解釋:
MyCalendar myCalendar = new MyCalendar();
myCalendar.book(10, 20); // return True
myCalendar.book(15, 25); // return False ,這個日程安排不能添加到日曆中,因為時間 15 已經被另一個日程安排預訂了。
myCalendar.book(20, 30); // return True ,這個日程安排可以添加到日曆中,因為第一個日程安排預訂的每個時間都小於 20 ,且不包含時間 20 。
提示:
- 0 <= start < end <= 109
- 每個測試用例,調用 book 方法的次數最多不超過 1000 次。
方法一:直接遍曆
我們記錄下所有已經預訂的課程安排區間,當我們預訂新的區間 [start,end) 時,此時檢查當前已經預訂的每個日程安排是否與新日程安排沖突。若不沖突,則可以添加新的日程安排。
- 對於兩個區間 [s1, e1)和 [s2, e2),如果二者沒有交集,則此時應當滿足 s1 ≥ e2 或者 s2 ≥ e1,這就意味著如果滿足 s1 < e2 並且 s2 < e1 ,則兩者會產生交集。
代碼:
class MyCalendar {
private:
vector<pair<int, int>> booked;
public:
MyCalendar() {
}
public:
bool book(int start, int end) {
for (auto &[l, r] : booked) {
if (l < end && start < r) {
return false;
}
}
booked.emplace_back(start, end);
return true;
}
};
執行用時:80 ms, 在所有 C++ 提交中擊敗了77.49%的用戶
內存消耗:36.6 MB, 在所有 C++ 提交中擊敗了97.08%的用戶
複雜度分析
時間複雜度:O(n2), 其中 n 錶示日程安排的數量。由於每次在進行預訂時,都需要遍曆所有已經預訂的行程安排。
空間複雜度: O(n),其中 n 錶示日程安排的數量。需要保存所有已經預訂的行程。
方法二:二分查找
如果我們按時間順序維護日程安排,則可以通過二分查找日程安排的情况來檢查新日程安排是否可以預訂,若可以預訂則在排序結構中更新插入日程安排。
- 需要一個數據結構能够保持元素排序和支持快速插入,可以用
TreeSet來構建。對於給定的區間[start,end),我們每次查找起點大於等於end的第一個區間 [ l1, r1 ),同時緊挨著 [ l1, r1) 的前一個區間為 [ l2, r2),此時如果滿足 r2 ≤ start < end ≤ l1 ,則該區間可以預訂。
代碼:
class MyCalendar {
private:
set<pair<int, int>> booked;
public:
MyCalendar() {
}
public:
bool book(int start, int end) {
auto it = booked.lower_bound({
end, 0});
if (it == booked.begin() || (--it)->second <= start) {
booked.emplace(start, end);
return true;
}
return false;
}
};
執行用時:64 ms, 在所有 C++ 提交中擊敗了98.77%的用戶
內存消耗:37.9 MB, 在所有 C++ 提交中擊敗了53.51%的用戶
複雜度分析
時間複雜度: O(nlogn), 其中 n 錶示日程安排的數量。由於每次在進行預訂時,都需要進行二分查找,需要的時間為 O(logn)。
空間複雜度: O(n),其中 n 錶示日程安排的數量。需要保存所有已經預訂的行程。
方法三:線段樹

代碼:
class MyCalendar {
unordered_set<int> tree, lazy;
public:
bool query(int start, int end, int l, int r, int idx) {
if (r < start || end < l) {
return false;
}
/* 如果該區間已被預訂,則直接返回 */
if (lazy.count(idx)) {
return true;
}
if (start <= l && r <= end) {
return tree.count(idx);
}
int mid = (l + r) >> 1;
return query(start, end, l, mid, 2 * idx) ||
query(start, end, mid + 1, r, 2 * idx + 1);
}
void update(int start, int end, int l, int r, int idx) {
if (r < start || end < l) {
return;
}
if (start <= l && r <= end) {
tree.emplace(idx);
lazy.emplace(idx);
} else {
int mid = (l + r) >> 1;
update(start, end, l, mid, 2 * idx);
update(start, end, mid + 1, r, 2 * idx + 1);
tree.emplace(idx);
if (lazy.count(2 * idx) && lazy.count(2 * idx + 1)) {
lazy.emplace(idx);
}
}
}
bool book(int start, int end) {
if (query(start, end - 1, 0, 1e9, 1)) {
return false;
}
update(start, end - 1, 0, 1e9, 1);
return true;
}
};
執行用時:476 ms, 在所有 C++ 提交中擊敗了5.03%的用戶
內存消耗:171.4 MB, 在所有 C++ 提交中擊敗了7.53%的用戶
边栏推荐
- SQL injection of cisp-pte (Application of secondary injection)
- 自己要有自己的坚持
- Games101 notes (II)
- sqlserver 做cdc 要对数据库性能有什么要求么
- Flet教程之 12 Stack 重叠组建图文混合 基础入门(教程含源码)
- [echart] resize lodash to realize chart adaptation when window is zoomed
- [js] 技巧 简化if 判空
- Using graylog alarm function to realize the regular work reminder of nail group robots
- [deep learning] [original] let yolov6-0.1.0 support the txt reading dataset mode of yolov5
- Cartoon: what is distributed transaction?
猜你喜欢
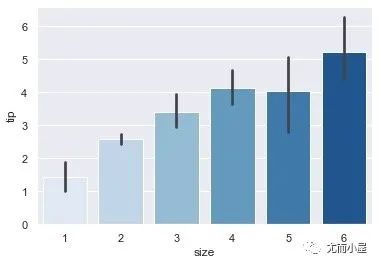
Seaborn绘制11个柱状图

Jarvis OJ Flag
![[team PK competition] the task of this week has been opened | question answering challenge to consolidate the knowledge of commodity details](/img/d8/a367c26b51d9dbaf53bf4fe2a13917.png)
[team PK competition] the task of this week has been opened | question answering challenge to consolidate the knowledge of commodity details
How to set the WiFi password of the router on the computer
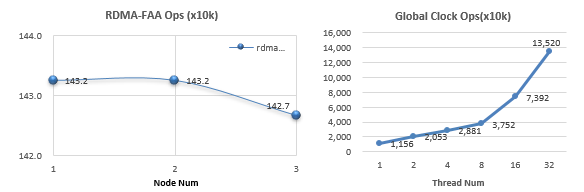
Hiengine: comparable to the local cloud native memory database engine

HiEngine:可媲美本地的云原生内存数据库引擎
Jarvis OJ 远程登录协议

Scratch colorful candied haws Electronic Society graphical programming scratch grade examination level 3 true questions and answers analysis June 2022
Jarvis OJ webshell analysis
StarkWare:欲构建ZK“宇宙”
随机推荐
[brush title] goose factory shirt problem
Using graylog alarm function to realize the regular work reminder of nail group robots
Practice independent and controllable 3.0 and truly create the open source business of the Chinese people
Jarvis OJ shell流量分析
挖财股票开户安全吗?怎么开股票账户是安全?
Win11如何给应用换图标?Win11给应用换图标的方法
Yarn common commands
Scratch colorful candied haws Electronic Society graphical programming scratch grade examination level 3 true questions and answers analysis June 2022
【刷题篇】鹅厂文化衫问题
How to install MySQL
详解SQL中Groupings Sets 语句的功能和底层实现逻辑
[js] skill simplification if empty judgment
Jarvis OJ webshell analysis
Single merchant v4.4 has the same original intention and strength!
Summary of PHP pseudo protocol of cisp-pte
Apple 已弃用 NavigationView,使用 NavigationStack 和 NavigationSplitView 实现 SwiftUI 导航
Clear restore the scene 31 years ago, volcanic engine ultra clear repair beyond classic concert
Migrate /home partition
scratch五彩糖葫芦 电子学会图形化编程scratch等级考试三级真题和答案解析2022年6月
Single merchant v4.4 has the same original intention and strength!
