当前位置:网站首页>4.1 Temporal Differential of one step
4.1 Temporal Differential of one step
2022-07-03 10:09:00 【Most appropriate commitment】
Catalog
Off-policy TD Control (Q-learning)
Definition
![v_{\pi_{t}}(s) \ \\ =\ E[ R_{t+1}+\gamma v_{ \pi_{t+1}} ] = \sum _a \pi(a|s) \sum _{r,s'}p(r,s'|s,a)(r+\gamma v(s')) =max_a \ \sum _{r,s'}p(r,s'|s,a)(r+\gamma v(s')) \\ =E[ G_t ] = average(G_t) \ in\ every\ s \\ \ =E[ R_{t+1}+\gamma G_{t+1} ]\approx average(R_{t+1}+\gamma v(s'))](http://img.inotgo.com/imagesLocal/202202/15/202202150539010219_10.gif)
![q_{\pi_t}(s,a) \\=E[R_{t+1}+\gamma q_{\pi_{t+1}}(s,a)]=\sum _{r,s'}p(r,s'|s,a)(r+\sum _{a'}\pi(a'|s')\gamma q(s',a')) = \sum _{r,s'}p(r,s'|s,a)(r+\gamma max_{a'} \ q(s',a')) \\=E[G_t(s,a)]=average(R_{t+1}+\gamma G_{t+1}(s,a)) \\=E[R_{t+1}+\gamma G_{t+1}]=average(R_{t+1}+\gamma q(S_{t+1},A_{t+1}))](http://img.inotgo.com/imagesLocal/202202/15/202202150539010219_15.gif)
Dynamic Programming uses the euqations in the second line and has to know the environmental dynamics ( dynamics of environemnt can produce the chain between this state to the next state, but it's hard to know. Cons ) ( It uses the relationship between different states, which creates bootstrapping. Experience from other states can be used in this state. Pros )
Monte Carlo Method uses the equations in the third line and has to know the returns from entire results ( which can produce the relationship between different states when we do not know the environmental dynamics Pros, and dynamics of environment may not precise as the Monte Carlo) ( However, when the episodes are not fully visited and updated, the values can only be updates partically )
Temporal Differential (shorten as TD) is the combination of DP and MC. First, it could update from other states, which means the states from A episode(not appear in B episide) can use the experience from B episide, because the value table is commonly used. It can avoid partially estimation from MC. Secondly, it uses the episodes from real world, we do not need the dynamics of programming.
Prediction of TD(0)
loop until the error < MINIMUM_OF_LIMIT:
v_last = v;
loop in the episode:
Choose action from policy in state, then get the reward and next state from episode;

error = maximum( |v - v_last| )
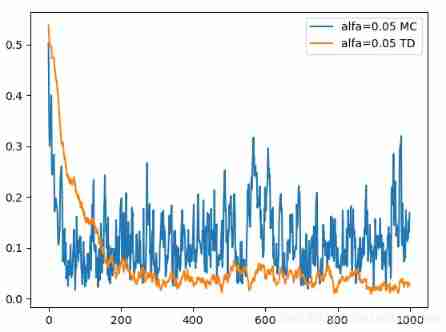
Random Walk
The result tells us TD is quiet greater than MC.



## settings
import math
import numpy as np
import random
# visualization
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
# INVARIANT
# state
STATE_LEFT = 0;
A = 1 ;
B = 2;
C = 3;
D = 4;
E = 5;
STATE_RIGHT = 6;
STATE =[ A,B,C,D,E ]
TERMINAL_STATE = [STATE_LEFT,STATE_RIGHT];
# action
LEFT = -1;
RIGHT = 1;
ACTION = [LEFT,RIGHT];
# random policy
random_policy = np.zeros((7,2),dtype = np.float);
for state in STATE:
random_policy[state][LEFT] = 0.5;
random_policy[state][RIGHT] = 0.5;
# discount
gamma = 1;
ALFA =[0.05,0.1,0.2];
# loop number
LOOP_EPISODE = 1000;
targets = [1.0/6,2.0/6,3.0/6,4.0/6,5.0/6]
# get reward
def get_reward(next_state):
return 1 if next_state==STATE_RIGHT else 0;
# get action
def get_action(state,policy):
p=[];
for action in ACTION:
p.append(policy[state][action]) ;
return np.random.choice(ACTION,p=p)
# Agent class
class Agent_class():
def __init__(self):
self.state_set=[];
self.reward_set=[];
self.current_state = C;
self.state_set.append(C);
def finish_sampling(self,policy):
while self.current_state in STATE:
action = get_action( self.current_state,policy );
self.current_state += action;
self.state_set.append(self.current_state);
self.reward_set.append(get_reward(self.current_state));
def get_rms(predictions,targets):
return np.sqrt( ((predictions-targets)**2).mean() );
for alfa in ALFA:
V_MC = np.zeros(7,dtype = np.float);
V_TD = np.zeros(7,dtype = np.float);
MC_RSM=[];
TD_RSM=[];
for every_loop in range(0,LOOP_EPISODE):
agent = Agent_class();
agent.finish_sampling(random_policy);
for state in range(0,len(agent.state_set)-1):
current_state = agent.state_set[state];
next_state = agent.state_set[state+1];
V_TD[current_state] = (1-alfa)*V_TD[ current_state ] + \
alfa*( agent.reward_set[state] + gamma *V_TD[ next_state ]);
G_t = agent.reward_set[-1];
for i in range(1,len(agent.state_set)):
current_state = agent.state_set[-i-1];
next_state = agent.state_set[-i];
V_MC[current_state] = (1-alfa)*V_MC[current_state] + \
alfa*gamma*G_t;
MC_RSM.append( get_rms(V_MC[1:6],targets) );
TD_RSM.append( get_rms(V_TD[1:6],targets) );
plt.plot(MC_RSM,'-',label='alfa='+str(alfa)+' MC');
plt.plot(TD_RSM,'-',label='alfa='+str(alfa)+' TD');
plt.legend();
plt.show()
'''
plt.plot(V_MC[1:6],label='alfa='+str(alfa)+' MC')
plt.plot(V_TD[1:6],label='alfa='+str(alfa)+' TD')
plt.legend();
plt.show()
'''
On-policy TD Control (Sarsa)

After every updation of every state in an episode, we could update the policy quickly rather than after every total episode in Monte Carlo.
Windy Gridworld
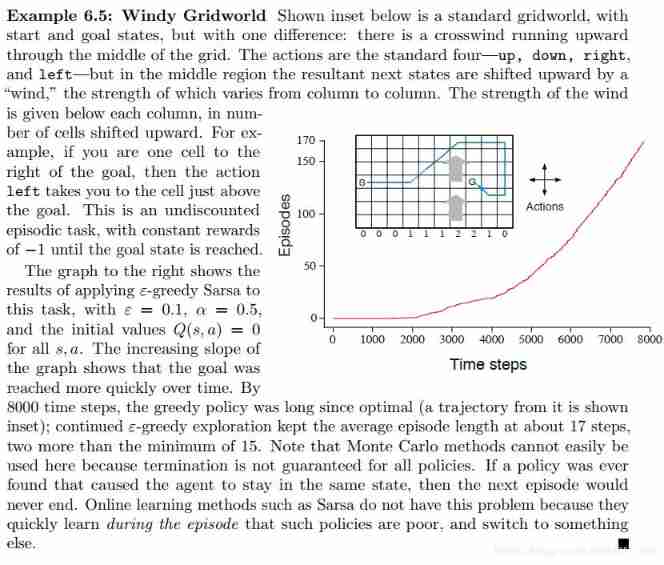 State: every position in this grid, the terminal state is the goal position.
State: every position in this grid, the terminal state is the goal position.
Action: left,right,up,down. there are some additional actions in the center of the gridworld.
reward: -1, until arrive at the terminal state.
policy evauluation: TD(0)
policy improvement: update after the iteration in every state
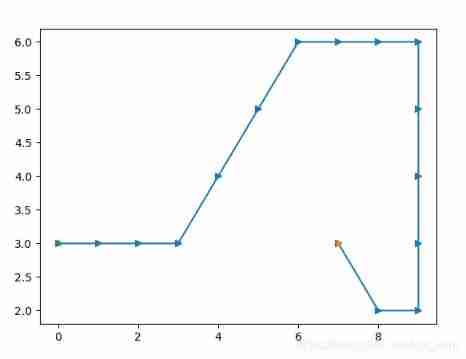
When soft-policy is applied (sigma=0.05,it's constant), we could get good result even optimal result sometimes.


When soft-policy is applied (sigma=0.05,it's decreasing from 0.05 to 0), we could get optimal result .

Code
## settings
import math
import numpy as np
import random
# visualization
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
# list copy
import copy
# INVARIANTS
#state (x,y)
STATE_INITIAL = (0,3);
STATE_GOAL = (7,3)
WIDTH = 10;
HEIGHT = 7;
# action
LEFT = (-1,0);
RIGHT = (1,0);
UP = (0,1);
DOWN = (0,-1);
ACTION_INTENDED = [LEFT,RIGHT,UP,DOWN];
# policy pi(a|s) which start at random policy, and updated after every iteration (function)
policy_target={}; # policy[(x,y)][action]
dict_actions_policy={};
for action in ACTION_INTENDED:
dict_actions_policy[action]=1/len(ACTION_INTENDED);
for x in range(0,WIDTH):
for y in range(0,HEIGHT):
policy_target[(x,y)] = copy.deepcopy(dict_actions_policy)
# reward: q_s_a(STATE_GOAL)=0, reward in every step is -1.
R = -1;
# special part: windy_effect, which will change the action_intended into action_actual
# there are different influence on different x.
# 1 unit influence will produce additional up in gridworld.
ACTION_WIND_EFFECT = [0,0,0,1,1,1,2,2,1,0];
# parameters we set
# sigma-policy
SIGMA = 0.05;
# number of episode
LOOP_EPISODE = 200;
# discounting parameter
gamma = 1;
# iteration step
alfa = 0.5;
# FUNCTIONS
# FUNCTIONS in policy evaluation
def choose_action(state,policy):
p=[];
index=range(0,len(ACTION_INTENDED));
for action in ACTION_INTENDED:
p.append(policy[state][action]);
action_intended = ACTION_INTENDED[np.random.choice(index,p=p)];
return action_intended;
# actual action taken (update after choice of actions )
def get_actual_action(state,action_intended):
x = action_intended[0]
y = action_intended[1] + ACTION_WIND_EFFECT[ state[0] ];
return ( (x,y) );
# state after the actual action taken
# the agent could not get out of the grid world.
def get_state_next(state,action):
state_next = ( state[0]+action[0], state[1]+action[1] );
x = max(state_next[0],0);
x = min(x,WIDTH-1);
y = max(state_next[1],0);
y = min(y,HEIGHT-1);
return (x,y);
# FUNCTIONS in policy improvement
# update after every iteration and use sigma-policy
def policy_updation(state,Q_s_a,policy):
Q=[];
for action in ACTION_INTENDED:
Q.append(Q_s_a[state][action]);
action_max = ACTION_INTENDED[np.argmax(Q)];
for action in ACTION_INTENDED:
policy[state][action] = sigma/len(ACTION_INTENDED);
policy[state][action_max] += 1 - sigma;
# CLASS
# CLASS Agent
class Agent_class():
def __init__(self):
# q_s_a[state][action] initial value =0;
self.Q_s_a={};
self.policy = copy.deepcopy( policy_target );
dict_q_action={};
for action in ACTION_INTENDED:
dict_q_action[action] = 0;
for x in range(0,WIDTH):
for y in range(0,HEIGHT):
self.Q_s_a[(x,y)] = copy.deepcopy( dict_q_action );
self.action_total_set=[];
self.state_total_set=[];
# current state
self.current_state = STATE_INITIAL;
# current action
self.current_intended_action = choose_action(self.current_state,self.policy)
self.current_actual_action = get_actual_action(self.current_state,self.current_intended_action);
def finish_journey(self):
# current state
self.current_state = STATE_INITIAL;
# current action
self.current_intended_action = choose_action(self.current_state,self.policy)
self.current_actual_action = get_actual_action(self.current_state,self.current_intended_action);
# state set and action set
action_set=[];
state_set=[];
action_set.append( self.current_intended_action );
state_set.append( self.current_state );
next_state = get_state_next(self.current_state,self.current_actual_action);
while next_state != STATE_GOAL:
# get the next action;
next_action_intended = choose_action(next_state,self.policy);
next_action_actual = get_actual_action(next_state,next_action_intended)
# policy evaluation
self.Q_s_a[self.current_state][self.current_intended_action] = (1-alfa)*\
self.Q_s_a[self.current_state][self.current_intended_action] + alfa* \
(R + self.Q_s_a[next_state][next_action_intended]);
#policy improvement
policy_updation(self.current_state,self.Q_s_a,self.policy)
# update current state and action
self.current_intended_action = next_action_intended;
self.current_actual_action = next_action_actual;
self.current_state = next_state;
# append of state set and action set
action_set.append( self.current_intended_action );
state_set.append( self.current_state );
# get next state
next_state = get_state_next(self.current_state,self.current_actual_action);
# update when next state is terminal state
state_set.append(next_state)
self.Q_s_a[self.current_state][self.current_intended_action] = (1-alfa)*\
self.Q_s_a[self.current_state][self.current_intended_action] + alfa* R;
self.action_total_set.append(action_set);
self.state_total_set.append(state_set);
def show_step(self):
x=[];
y=[];
for state in self.state_total_set[-1]:
x.append(state[0]);
y.append(state[1]);
plt.plot(x,y,'->')
plt.plot(STATE_GOAL[0],STATE_GOAL[1],'*')
plt.plot(STATE_INITIAL[0],STATE_INITIAL[1],'*')
plt.show();
def show_step_number_of_every_episode(self):
number=[];
for i in range(0,len(self.action_total_set)):
number.append(len(self.action_total_set[i]));
plt.plot(number,'-*')
plt.xlabel('number of episodes')
plt.ylabel('number of steps')
plt.show();
# main programming
agent = Agent_class();
for every_loop in range(0,LOOP_EPISODE):
#sigma = SIGMA*(LOOP_EPISODE-every_loop)/LOOP_EPISODE;
sigma = SIGMA;
agent.finish_journey();
agent.show_step();
agent.show_step_number_of_every_episode();
Off-policy TD Control (Q-learning)

Result
When soft-policy is applied (sigma=0.05,constant), we could get good result . Because it will have some non-perfect actions.
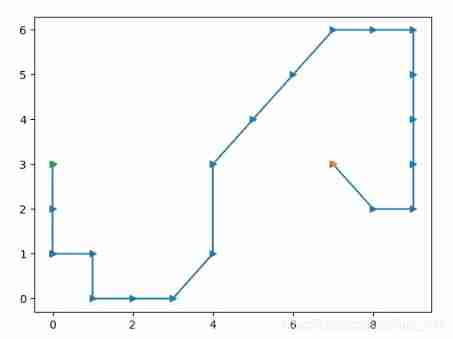
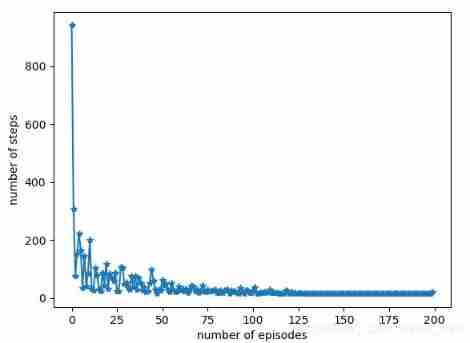
When soft-policy is applied (sigma=0.05,it's decreasing from 0.05 to 0), we could get optimal result . But more episodes are needed than Sarsa.




Code
## settings
import math
import numpy as np
import random
# visualization
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
# list copy
import copy
# INVARIANTS
#state (x,y)
STATE_INITIAL = (0,3);
STATE_GOAL = (7,3)
WIDTH = 10;
HEIGHT = 7;
# action
LEFT = (-1,0);
RIGHT = (1,0);
UP = (0,1);
DOWN = (0,-1);
ACTION_INTENDED = [LEFT,RIGHT,UP,DOWN];
# policy pi(a|s) which start at random policy, and updated after every iteration (function)
policy_target={}; # policy[(x,y)][action]
dict_actions_policy={};
for action in ACTION_INTENDED:
dict_actions_policy[action]=1/len(ACTION_INTENDED);
for x in range(0,WIDTH):
for y in range(0,HEIGHT):
policy_target[(x,y)] = copy.deepcopy(dict_actions_policy)
# reward: q_s_a(STATE_GOAL)=0, reward in every step is -1.
R = -1;
# special part: windy_effect, which will change the action_intended into action_actual
# there are different influence on different x.
# 1 unit influence will produce additional up in gridworld.
ACTION_WIND_EFFECT = [0,0,0,1,1,1,2,2,1,0];
# parameters we set
# sigma-policy
SIGMA = 0.05;
# number of episode
LOOP_EPISODE = 100;
# discounting parameter
gamma = 1;
# iteration step
alfa = 0.5;
# FUNCTIONS
# FUNCTIONS in policy evaluation
def choose_action(state,policy):
p=[];
index=range(0,len(ACTION_INTENDED));
for action in ACTION_INTENDED:
p.append(policy[state][action]);
action_intended = ACTION_INTENDED[np.random.choice(index,p=p)];
return action_intended;
def choose_max_action(state,Q_s_a):
Q=[];
choice=[];
for action in ACTION_INTENDED:
Q.append(Q_s_a[state][action]);
for i in range(0,len(Q)):
if Q[i]==max(Q):
choice.append(ACTION_INTENDED[i]);
action_max = random.choice(choice);
return action_max;
# actual action taken (update after choice of actions )
def get_actual_action(state,action_intended):
x = action_intended[0]
y = action_intended[1] + ACTION_WIND_EFFECT[ state[0] ];
return ( (x,y) );
# state after the actual action taken
# the agent could not get out of the grid world.
def get_state_next(state,action):
state_next = ( state[0]+action[0], state[1]+action[1] );
x = max(state_next[0],0);
x = min(x,WIDTH-1);
y = max(state_next[1],0);
y = min(y,HEIGHT-1);
return (x,y);
# FUNCTIONS in policy improvement
# update after every iteration and use sigma-policy
def policy_updation(state,Q_s_a,policy):
Q=[];
for action in ACTION_INTENDED:
Q.append(Q_s_a[state][action]);
action_max = ACTION_INTENDED[np.argmax(Q)];
for action in ACTION_INTENDED:
policy[state][action] = sigma/len(ACTION_INTENDED);
policy[state][action_max] += 1 - sigma;
# CLASS
# CLASS Agent
class Agent_class():
def __init__(self):
# q_s_a[state][action] initial value =0;
self.Q_s_a={};
self.policy = copy.deepcopy( policy_target );
dict_q_action={};
for action in ACTION_INTENDED:
dict_q_action[action] = 0;
for x in range(0,WIDTH):
for y in range(0,HEIGHT):
self.Q_s_a[(x,y)] = copy.deepcopy( dict_q_action );
self.action_total_set=[];
self.state_total_set=[];
# current state
self.current_state = STATE_INITIAL;
# current action
self.current_intended_action = choose_action(self.current_state,self.policy)
self.current_actual_action = get_actual_action(self.current_state,self.current_intended_action);
def finish_journey(self):
# current state
self.current_state = STATE_INITIAL;
# current action
self.current_intended_action = choose_action(self.current_state,self.policy)
self.current_actual_action = get_actual_action(self.current_state,self.current_intended_action);
# state set and action set
action_set=[];
state_set=[];
action_set.append( self.current_intended_action );
state_set.append( self.current_state );
next_state = get_state_next(self.current_state,self.current_actual_action);
while next_state != STATE_GOAL:
# get the next action;
next_action_intended = choose_max_action(next_state,self.Q_s_a);
next_action_actual = get_actual_action(next_state,next_action_intended)
# policy evaluation
self.Q_s_a[self.current_state][self.current_intended_action] = (1-alfa)*\
self.Q_s_a[self.current_state][self.current_intended_action] + alfa* \
(R + self.Q_s_a[next_state][next_action_intended]);
#policy improvement
policy_updation(self.current_state,self.Q_s_a,self.policy)
# update current state and action
self.current_intended_action = next_action_intended;
self.current_actual_action = next_action_actual;
self.current_state = next_state;
# append of state set and action set
action_set.append( self.current_intended_action );
state_set.append( self.current_state );
# get next state
next_state = get_state_next(self.current_state,self.current_actual_action);
# update when next state is terminal state
state_set.append(next_state)
self.Q_s_a[self.current_state][self.current_intended_action] = (1-alfa)*\
self.Q_s_a[self.current_state][self.current_intended_action] + alfa* R;
self.action_total_set.append(action_set);
self.state_total_set.append(state_set);
def show_step(self):
x=[];
y=[];
for state in self.state_total_set[-1]:
x.append(state[0]);
y.append(state[1]);
plt.plot(x,y,'->')
plt.plot(STATE_GOAL[0],STATE_GOAL[1],'*')
plt.plot(STATE_INITIAL[0],STATE_INITIAL[1],'*')
plt.show();
def show_step_number_of_every_episode(self):
number=[];
for i in range(0,len(self.action_total_set)):
number.append(len(self.action_total_set[i]));
plt.plot(number,'-*')
plt.xlabel('number of episodes')
plt.ylabel('number of steps')
plt.show();
# main programming
agent = Agent_class();
for every_loop in range(0,LOOP_EPISODE):
sigma = SIGMA*(LOOP_EPISODE-every_loop)/LOOP_EPISODE;
#sigma = SIGMA;
agent.finish_journey();
agent.show_step();
agent.show_step_number_of_every_episode();
Expected Sarsa

If we select actions in soft-greedy policy and use this policy to update Q, then it will be on-policy expected Sarsa.
If we select actions in non-greedy policy and use greedy policy to update Q, then expected Sarsa will be Q-learning.
Result
when sigma = 0.1, the influence of differnent alfa in different algorithom:
Sarsa algorithon is not stable when alfa is large such as 0.9. But Q-learning and Expected Sarsa are stable.


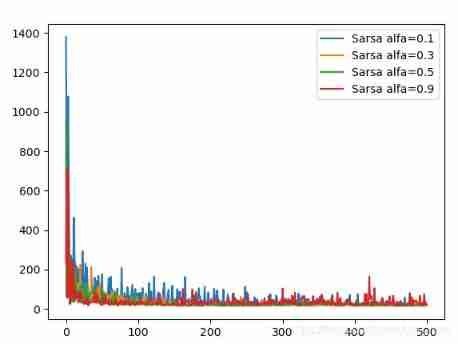
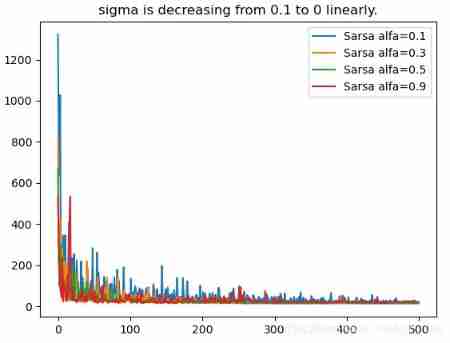
Code
## settings
import math
import numpy as np
import random
# visualization
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
# list copy
import copy
# INVARIANTS
#state (x,y)
STATE_INITIAL = (0,3);
STATE_GOAL = (7,3)
WIDTH = 10;
HEIGHT = 7;
# action
LEFT = (-1,0);
RIGHT = (1,0);
UP = (0,1);
DOWN = (0,-1);
ACTION_INTENDED = [LEFT,RIGHT,UP,DOWN];
# policy pi(a|s) which start at random policy, and updated after every iteration (function)
policy_target={}; # policy[(x,y)][action]
dict_actions_policy={};
for action in ACTION_INTENDED:
dict_actions_policy[action]=1/len(ACTION_INTENDED);
for x in range(0,WIDTH):
for y in range(0,HEIGHT):
policy_target[(x,y)] = copy.deepcopy(dict_actions_policy)
# reward: q_s_a(STATE_GOAL)=0, reward in every step is -1.
R = -1;
# special part: windy_effect, which will change the action_intended into action_actual
# there are different influence on different x.
# 1 unit influence will produce additional up in gridworld.
ACTION_WIND_EFFECT = [0,0,0,1,1,1,2,2,1,0];
# parameters we set
# sigma-policy
SIGMA = 0.1;
# number of episode
LOOP_EPISODE = 500;
# discounting parameter
gamma = 1;
# iteration step
ALFA =[ 0.1,0.3,0.5,0.9];
# FUNCTIONS
# FUNCTIONS in policy evaluation
def choose_action(state,policy):
p=[];
index=range(0,len(ACTION_INTENDED));
for action in ACTION_INTENDED:
p.append(policy[state][action]);
action_intended = ACTION_INTENDED[np.random.choice(index,p=p)];
return action_intended;
def choose_max_action(state,Q_s_a):
Q=[];
choice=[];
for action in ACTION_INTENDED:
Q.append(Q_s_a[state][action]);
for i in range(0,len(Q)):
if Q[i]==max(Q):
choice.append(ACTION_INTENDED[i]);
action_max = random.choice(choice);
return action_max;
# actual action taken (update after choice of actions )
def get_actual_action(state,action_intended):
x = action_intended[0]
y = action_intended[1] + ACTION_WIND_EFFECT[ state[0] ];
return ( (x,y) );
# state after the actual action taken
# the agent could not get out of the grid world.
def get_state_next(state,action):
state_next = ( state[0]+action[0], state[1]+action[1] );
x = max(state_next[0],0);
x = min(x,WIDTH-1);
y = max(state_next[1],0);
y = min(y,HEIGHT-1);
return (x,y);
# FUNCTIONS in policy improvement
# update after every iteration and use sigma-policy
def policy_updation(state,Q_s_a,policy):
Q=[];
for action in ACTION_INTENDED:
Q.append(Q_s_a[state][action]);
actions_max = [];
for i in range(0,len(ACTION_INTENDED)):
if Q_s_a[state][ACTION_INTENDED[i]]==max(Q):
actions_max.append(ACTION_INTENDED[i]);
action_max = random.choice(actions_max);
for action in ACTION_INTENDED:
policy[state][action] = sigma/len(ACTION_INTENDED);
policy[state][action_max] += 1 - sigma;
# CLASS
# CLASS Agent
class Agent_class():
def __init__(self):
# q_s_a[state][action] initial value =0;
self.Q_s_a={};
self.policy = copy.deepcopy( policy_target );
dict_q_action={};
for action in ACTION_INTENDED:
dict_q_action[action] = 0;
for x in range(0,WIDTH):
for y in range(0,HEIGHT):
self.Q_s_a[(x,y)] = copy.deepcopy( dict_q_action );
self.action_total_set=[];
self.state_total_set=[];
self.step_number_in_episode={};
# current state
self.current_state = STATE_INITIAL;
# current action
self.current_intended_action = choose_action(self.current_state,self.policy)
self.current_actual_action = get_actual_action(self.current_state,self.current_intended_action);
def finish_journey(self):
# current state
self.current_state = STATE_INITIAL;
# current action
self.current_intended_action = choose_action(self.current_state,self.policy);
self.current_actual_action = get_actual_action(self.current_state,self.current_intended_action);
# state set and action set
action_set=[];
state_set=[];
action_set.append( self.current_intended_action );
state_set.append( self.current_state );
next_state = get_state_next(self.current_state,self.current_actual_action);
while next_state != STATE_GOAL:
# policy evaluation average of every action
Q_temp= (1-alfa)*self.Q_s_a[self.current_state][self.current_intended_action]\
+alfa*R;
for action in ACTION_INTENDED:
Q_temp+= alfa*self.Q_s_a[next_state][action]*self.policy[next_state][action];
self.Q_s_a[self.current_state][self.current_intended_action]=Q_temp;
#policy improvement
policy_updation(self.current_state,self.Q_s_a,self.policy)
# get the next action;
next_action_intended = choose_max_action(next_state,self.Q_s_a);
next_action_actual = get_actual_action(next_state,next_action_intended)
# update current state and action
self.current_intended_action = next_action_intended;
self.current_actual_action = next_action_actual;
self.current_state = next_state;
# append of state set and action set
action_set.append( self.current_intended_action );
state_set.append( self.current_state );
# get next state
next_state = get_state_next(self.current_state,self.current_actual_action);
# update when next state is terminal state
state_set.append(next_state)
self.Q_s_a[self.current_state][self.current_intended_action] = (1-alfa)*\
self.Q_s_a[self.current_state][self.current_intended_action] + alfa* R;
self.action_total_set.append(action_set);
self.state_total_set.append(state_set);
def show_step(self):
x=[];
y=[];
for state in self.state_total_set[-1]:
x.append(state[0]);
y.append(state[1]);
plt.plot(x,y,'->')
plt.plot(STATE_GOAL[0],STATE_GOAL[1],'*')
plt.plot(STATE_INITIAL[0],STATE_INITIAL[1],'*')
plt.show();
def step_number_of_every_episode(self):
number=[];
for i in range(0,len(self.action_total_set)):
number.append(len(self.action_total_set[i]));
self.step_number_in_episode=number;
def show_step_number_of_every_episode(self):
number=[];
for i in range(0,len(self.action_total_set)):
number.append(len(self.action_total_set[i]));
plt.plot(number,'-*')
plt.xlabel('number of episodes')
plt.ylabel('number of steps')
plt.show();
# main programming
number_set =[];
for alfa in ALFA:
agent = Agent_class();
for every_loop in range(0,LOOP_EPISODE):
#sigma = SIGMA*(LOOP_EPISODE-every_loop)/LOOP_EPISODE;
sigma = SIGMA;
agent.finish_journey();
#agent.show_step();
agent.step_number_of_every_episode();
number_set.append(agent.step_number_in_episode);
for i in range(0,len(ALFA)):
plt.plot(number_set[i],label='expected Sarsa '+'alfa='+str(ALFA[i]))
plt.legend();
plt.show();
边栏推荐
- getopt_ Typical use of long function
- Pycharm cannot import custom package
- LeetCode - 919. 完全二叉树插入器 (数组)
- CV learning notes ransca & image similarity comparison hash
- Opencv interview guide
- 2312、卖木头块 | 面试官与狂徒张三的那些事(leetcode,附思维导图 + 全部解法)
- 03 FastJson 解决循环引用
- There is no shortcut to learning and development, and there is almost no situation that you can learn faster by leading the way
- Tensorflow2.0 save model
- Interruption system of 51 single chip microcomputer
猜你喜欢
Leetcode - 1670 design front, middle and rear queues (Design - two double ended queues)
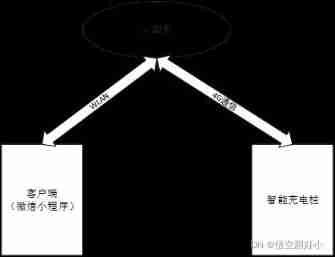
Development of intelligent charging pile (I): overview of the overall design of the system
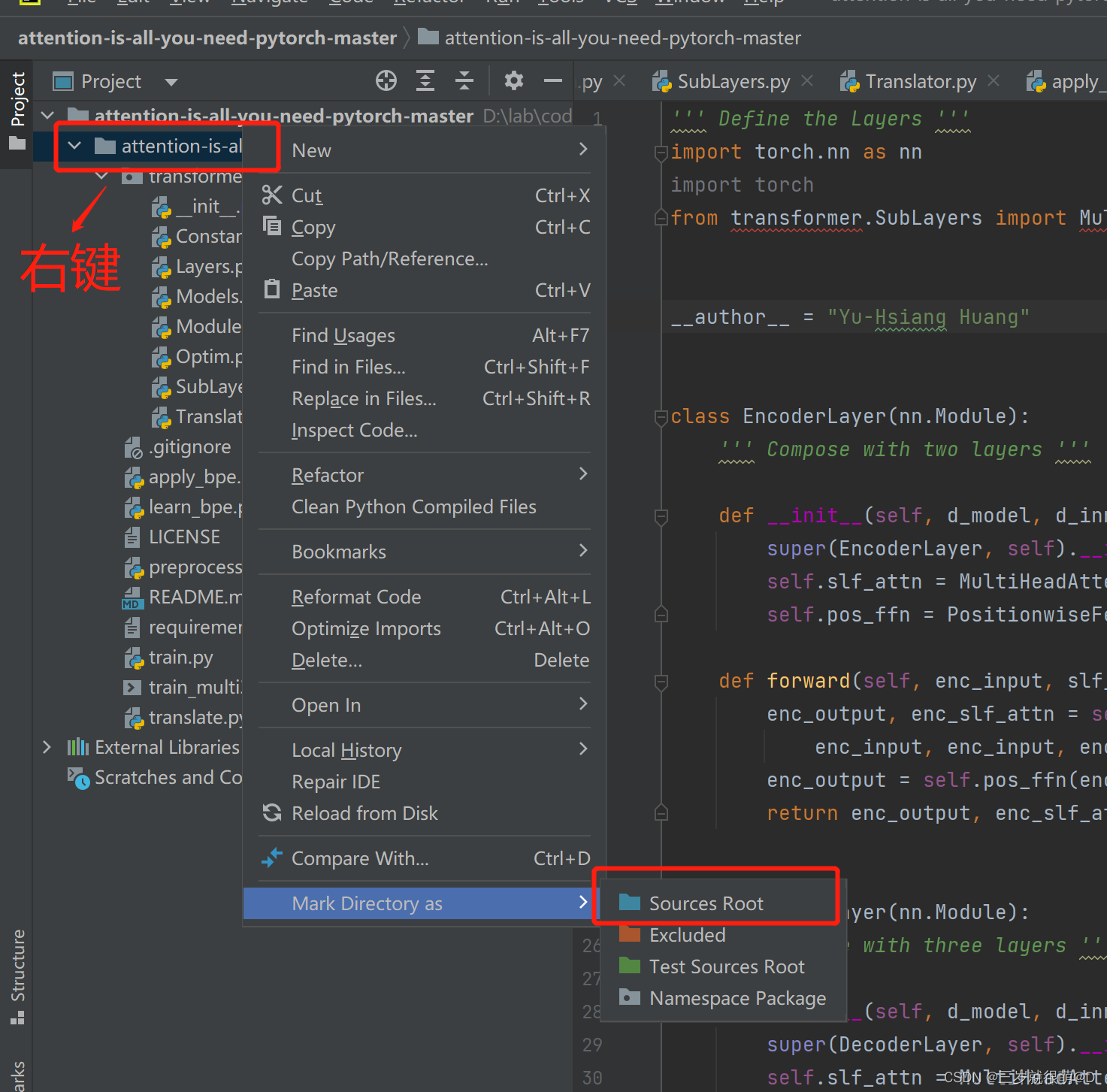
Pycharm cannot import custom package

Yocto Technology Sharing Phase 4: Custom add package support
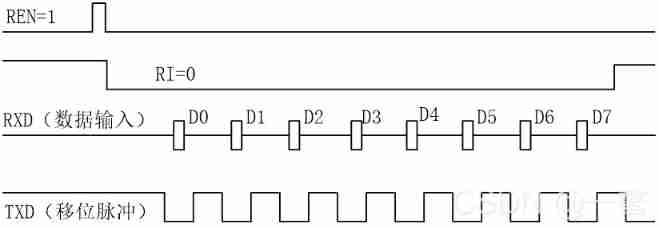
Working mode of 80C51 Serial Port

Leetcode 300 longest ascending subsequence

Opencv note 21 frequency domain filtering

Swing transformer details-2

CV learning notes alexnet

Leetcode - 1670 conception de la file d'attente avant, moyenne et arrière (conception - deux files d'attente à double extrémité)
随机推荐
. DLL and Differences between lib files
The data read by pandas is saved to the MySQL database
2021-10-27
Connect Alibaba cloud servers in the form of key pairs
Toolbutton property settings
Working mode of 80C51 Serial Port
03 FastJson 解决循环引用
RESNET code details
20220605数学:两数相除
Leetcode 300 最长上升子序列
2312. Selling wood blocks | things about the interviewer and crazy Zhang San (leetcode, with mind map + all solutions)
Sending and interrupt receiving of STM32 serial port
Qcombox style settings
Openeuler kernel technology sharing - Issue 1 - kdump basic principle, use and case introduction
LeetCode - 919. Full binary tree inserter (array)
LeetCode - 706 设计哈希映射(设计) *
My notes on the development of intelligent charging pile (III): overview of the overall design of the system software
Application of 51 single chip microcomputer timer
2. Elment UI date selector formatting problem
JS foundation - prototype prototype chain and macro task / micro task / event mechanism