当前位置:网站首页>Logic of automatic reasoning 06 -- predicate calculus
Logic of automatic reasoning 06 -- predicate calculus
2022-07-24 11:03:00 【Hard working K cub】
Logic of automatic reasoning 06– Predicate calculus
review : Functions and relationships
A collection A = {a1, . . . , an, . . . } It's the object a1, a2, Set . . .
Predicate logical alphabet
The alphabet of predicate logic consists of
1 .( Countable infinity ) Logical variable x、y、z、x1、x2 Set V.
2. Set up F = {f1, f2, . . . } A fixed number of function symbols
3. Set up P = {P1, P2, . . . } A fixed number of predicates / Relational symbols
4. Predicate symbols =
5. Conjunctions ⊥、>、¬、∧、∨、→、∀、∃
6. Auxiliary symbols 、 etc.
A signature is a collection of functional and relational symbols .
examples:
1 signature of arithmetic: ΣA = {+, ·, 0, 1}
2 signature of boolean algebras: ΣBA = {u, t, −, 0, 1}
3 signature of graphs: ΣG = {E}
Clause Terms
Signing at Σ Upper Σ Collection of items TΣ Defined by grammar
t ::= x | f (t1, … ,tn)
x It's a variable. ,f Are some elements n and t1 Function symbol for ,. . . ,tn yes Σ term .
In especial
1 Every variable x And a constant sign c All one item .
2 take f (t1, … ,tn) Applies to the term t1, . . . ,tn It's a term .
3 There are no other terms .
Items without variables are base items
Example : The arithmetic
Sign with constant 2, 3, 4, Expand ΣA. . . about N Each element of , Give Way x, y ∈ V, that
3 + 5 · 7 x + 5 · y It's an arithmetic term
example: boolean algebra
extend ΣBA with constant symbols a and b, then
a n −a
a
a u (b n −a)
are terms of boolean algebra
Example :
Consider signing {MotherOf , Alice, Betty}, then
MotherOf( Alice ) And Betty are terms
The term is not evaluated as true or false , But other values , for example Numbers
Variables are simple pointers to values , A term is a complex pointer to a value
for example ,MotherOf (Alice) It can be evaluated as Betty
The formula Formulas
for all t1, . . .tn ∈ TΣ and P ∈ P of arity n,
ΦΣ ::=⊥ | T | t1 = t2 | P(t1, . . . ,tn) | (¬ΦΣ) | (ΦΣ ∧ ΦΣ) | (ΦΣ ∨ ΦΣ) | (ΦΣ → ΦΣ) | (∀x. ΦΣ) | (∃x. ΦΣ)
⊥, T, t1 = t2 and P(t1, . . . ,tn) It's the atomic formula
Everything else is compound
example:
∀P. (P(0) ∧ ∀k. P(k) → P(k + 1)) → ∀n. P(n)) Not a formula of predicate logic , It quantifies predicates, and operator precedence helps minimize the number of parentheses
examples:
1 ∃x. Loves(x, Bob) (somebody loves Bob)
2 ∃x. Loves(Alice, x) (Alice loves someone)
3 ¬∃x. Loves(x, Bob) (nobody loves Bob)
4 ∀x. Loves(x, Alice) (everybody loves Alice)
5 ¬∀x. Loves(x, Bob) (not everybody loves Bob)
6 ∀x∃y. Loves(x, y) (everybody loves somebody)
7 ∃x∀y. Loves(x, y) (somebody loves everybody)
Free and bound variables
Quantifiers provide scope for variables
Like a local variable, it has a range within a code block
function V : T → P(V) defined by
V(x) = {x}
V = ∅
V(f (t1, . . . ,tn)) = V(t1) ∪ · · · ∪ V(tn)
Calculates a set of variables that appear in a given term
If x ∈ V(t),x Appears in terms t, Its extension to the formula is obvious ( Equals the set of variables in the leaves of its syntax tree )
But please pay attention to :V(∃x.φ) = V(∀x.φ) = V(φ)
A variable may appear more than once in a formula
Example :x Three times
∀x. ((P(x) → Q(x)) ∧ R(x, f (y, z)))
If x Appears in the sub formula ∀x .ψ or ∃x.ψ in , be x stay φ It is inevitable that .
If x Not bound , It's in φ What happened in x It's free
A formula in which all variables are bound is closed / A sentence
Example :
∀x.((P(x) -> Q(x) ∧ R (x, f(y,z))
All that appears x Is bound. ; y and z Those of are free
x stay ∀x There is a free and bounded appearance in .∀x. P(x) ∧ Q(x)
the function FV : Φ → P(V) defined by
FV(⊥) = ∅
FV(T) = ∅
FV(t1 = t2) = V(t1) ∪ V(t2)
FV(P(t1, . . .tn)) = V(t1) ∪ · · · ∪ V(tn)
FV(¬ϕ) = FV(ϕ)
FV(ϕ ψ) = FV(ϕ) ∪ FV(ψ) if ∈ {
∧, ∨, →}
FV(Qx. ϕ) = FV(ϕ) − {
x} if Q ∈ {
∀, ∃}
replace Substitution
Replace replace variables in the formula by items
They are Φ → Φ Function of type , Completely by “ smaller ” decision V → T Type of function
We write ϕ[t/x] It means that you will t Replace with φ All free to appear in x Result
for terms s,t ∈ T , s[t/x] is defined by
y[t/x] =y if x /= y if s = y
=t if x = y if s = y
c[t/x] = c if s = c
f (t1, . . . ,tn)[t/x] = f (t1[t/x], . . .tn[t/x])
if s = f (t1, . . . ,tn)
for t ∈ T and ϕ ∈ Φ, ϕ[t/x] is defined by
[t/x] = T if ϕ = T
⊥[t/x] = ⊥ if ϕ = ⊥
P(t1, . . . ,tn)[t/x] = P(t1[t/x], . . . ,tn[t/x])
if ϕ = P(t1, . . . ,tn)
(s1 = s2)[t/x] = (s1[t/x] = s2[t/x]) if ϕ = (s1 = s2)
for t ∈ T and ϕ ∈ Φ, ϕ[t/x] is defined by
(¬ψ)[t/x] = ¬(ψ[t/x]) if ϕ = ¬ψ
(ψ1 ψ2)[t/x] = ψ1[t/x] ψ2[t/x]
if ϕ = ψ1 ψ2 for ∈ {
∧, ∨, →}
(Qy. ψ)[t/x] = Qy. (ψ[t/x]) if x /= y
= Qy. ψ if x = y
if ϕ = Qy. ψ for Q ∈ {
∀, ∃}
examples:
1 P(x)[a/x] = P(a)
2 P(x, y)[f (y, y)/x] = P(f (y, y), y)
3 ((∀x. P(x)) ∧ Q(x))[c/x] = ∀x. P(x) ∧ Q
4 P(x)[f (y)/x][a/y] = P(f (y))[a/y] = P(f (a))
Variable capture
Substitution may result in variable capture
Example :
(∀x. P(x, y))[f(x)/y] = ∀x. P(x, f(x))
P The second parameter of is not in... Before replacement ∀x Within the scope of , But after it, variable capture occurs when variables in terms are replaced with some variables , Variables become bound after replacement
For the formula φ The variables in the x, term t It's free
If t The variables in will t Replace with φ Medium x Not after φ In the binding , Formal definitions can be found
Example :
1 y is free for x in ∃z. P(x, z)
2 f (x, y) is not free for x in ∃y. P(x, y)
3 v is free for x in P(x, z) → ∀x. Q(x, y)
If t Yes φ Medium x It's free , We only use t Instead of φ Medium x
Review of deductive system
We extend the term syntax to natural deductive parameters
t ::= x | a | f (t, … ,t)
among a From a countable infinite set of parameters
--a
.
.
.
ϕ[a/x]
---------------- ∀I
∀x. ϕ
∀x. ϕ
-------------- ∀E
ϕ[t/x]
ϕ[t/x]
--------------- ∃I
∃x. ϕ
t1 = t2 ϕ[t1/x]
---------------------- =E
ϕ[t2/x]
among t1 and t2 about φ Medium x It's free
We can now replace non base items in deductions , Renamed appropriately
structure
NOTES
Model Models
Model (Γ) It's a structure , The given sentence set (Γ) Establishment is the same as propositional logic , We explain the formula in the structure , To check whether these formulas are models
Example : We use the language of Boolean algebra to explain formulas .
∀x. x n −x = 0
∀x∀y. x u y = y u x
− 0 = 1
In power set Boolean algebra , Check whether they are in this structure :
BA = (P(A), ∩, ∪, −, ∅, A)
Explanation of terms and formulas Interpretation of Terms and Formulas
Notes
Model class
A set of sentences Γ ⊆ Φ The model class of consists of all structures A form , bring A |= Γ
If we have a logical sum Mod(Γ) By Γ Axiomatic model classes :
We can use Γ |- φ To study Mod(Γ) Properties of the model in .
Example of model class :
Model classes of sentences
∀x. x ≤ x( reflexivity reflexivity)
∀x∀y. x ≤ y ∧ y ≤ x → x = y( antisymmetric antisymmetry)
∀x∀y∀z. x ≤ y ∧ y ≤ z → x ≤ y( Transitivity transitivity)
Are all partially ordered classes
Sentences that represent a kind of structure are axioms of that kind
** MAO semigroup (monoid)** Is a structure that satisfies axioms (M, ·, e)
∀x∀y∀z. x · (y · z) = (x · y) · z
∀x. e · x = x
∀x. x · e = x
The specific model is : Add and 1 Natural number under ; function f : A → A In function combination and identity function idA Next
When axioms are universally quantified , Quantifiers are usually deleted
** Ring (ring)** Is a structure that satisfies axioms (R, +, ·, −, 0, 1)
x + (y + z) = (x + y) + z
x + 0 = x
x + (−x) = 0
x · (y · z) = (x · y) · z
x · (y + z) = x · y + x · z
The specific model is : Integer under standard arithmetic operation ; R Upper n × n matrix
** Boolean algebra (boolean algebra)** Is a structure that satisfies axioms (B, n, u, −, 0, 1)
x n (y n z) = (x n y) n z
x u (y u z) = (x u y) u z
x u 0 = x
x n 1 = x
x u (y n z) = (x n y) u (x n z)
x u (−x) = 1
x n (−x) = 1
Effectiveness and applicability Validity and Entailment
If A |= φ For all structures A, The sentence φ ∈ Φ It works
If φ It works , We write |= φ
aggregate Γ ⊆ Φ Sentences ( Semantically ) Include sentences ϕ ∈ Φ, If Γ Every model of is ϕ Model of
It means A |= Γ signify A |= φ For each structure A
We write Γ |= φ If Γ contains φ
Satisfiability
If A |= φ For a structure A, The sentence φ ∈ Φ Is satisfiable
φ Unsatisfiable ( contradiction ), If it is unsatisfiable
Conjecture and refutation Conjectures and Refutations
Models can provide counterexamples for effectiveness
In Mathematics / In computational modeling , This is for exploring conjectures , Test the hypothesis , Analyze system specifications , Debugging code is important
Verifying a conjecture requires proof , Falsification is a counter example
Example :
The sentence ∃x∀y.P(x, y) → ∀y∃x.P(x, y) It works , We can use natural deduction to prove
The sentence ∀x∃y. P(x, y) → ∃y∀x. P(x, y) Invalid , We need a counterexample —— One is that it is a false structure
in fact ,N≤ /|= ∀x∃y. x ≤ y → ∃y∀x. x ≤ y stay N In the ordered arithmetic of
N There is no largest natural number in , So the former is true , The latter is false
边栏推荐
- Openresty Lua resty logger socket log transfer
- web咸鱼自救攻略--typescript的类没有你想象中的那么难
- Zero basic learning canoe panel (7) -- input/output box
- [micro service] eureka+ribbon realizes registration center and load balancing
- No one knows what ingredients tiktok's latest popular product pink sauce contains
- [FPGA]: frequency measurement
- The bean injected through @autowired can still be injected even if the class is not annotated with annotations such as @comment
- Detailed explanation of the implementation process of redistribution watchdog
- Windows virtual machine security reinforcement process steps, detailed description of windows setting security policy, detailed description of win7 setting IP security policy, windows setting firewall
- LoRa无线技术与LoRaWAN网关模块的区别
猜你喜欢

Cookie sessionstorage localstorage differences

零基础学习CANoe Panel(3)—— 静态控件(Static Text , Group Box ,Picture Box)

Overview of basic knowledge of binary tree

蓝牙模块的5大应用场景

Windows virtual machine security reinforcement process steps, detailed description of windows setting security policy, detailed description of win7 setting IP security policy, windows setting firewall
![[FPGA]: IP core --divider (divider)](/img/bc/d8b7638e236c468ba23c8afc7ab70e.png)
[FPGA]: IP core --divider (divider)
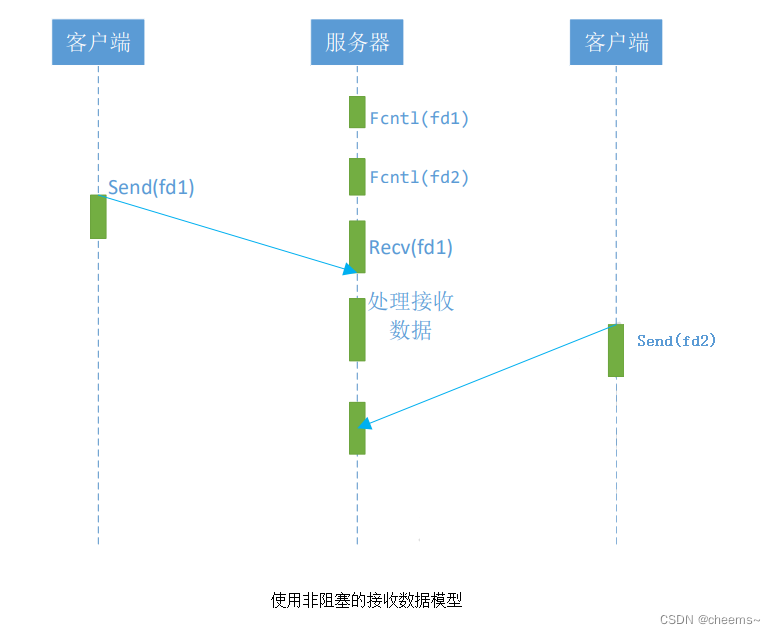
Five network IO models

零基础学习CANoe Panel(7)—— 文件选择(PathDiaglog)

No one knows what ingredients tiktok's latest popular product pink sauce contains
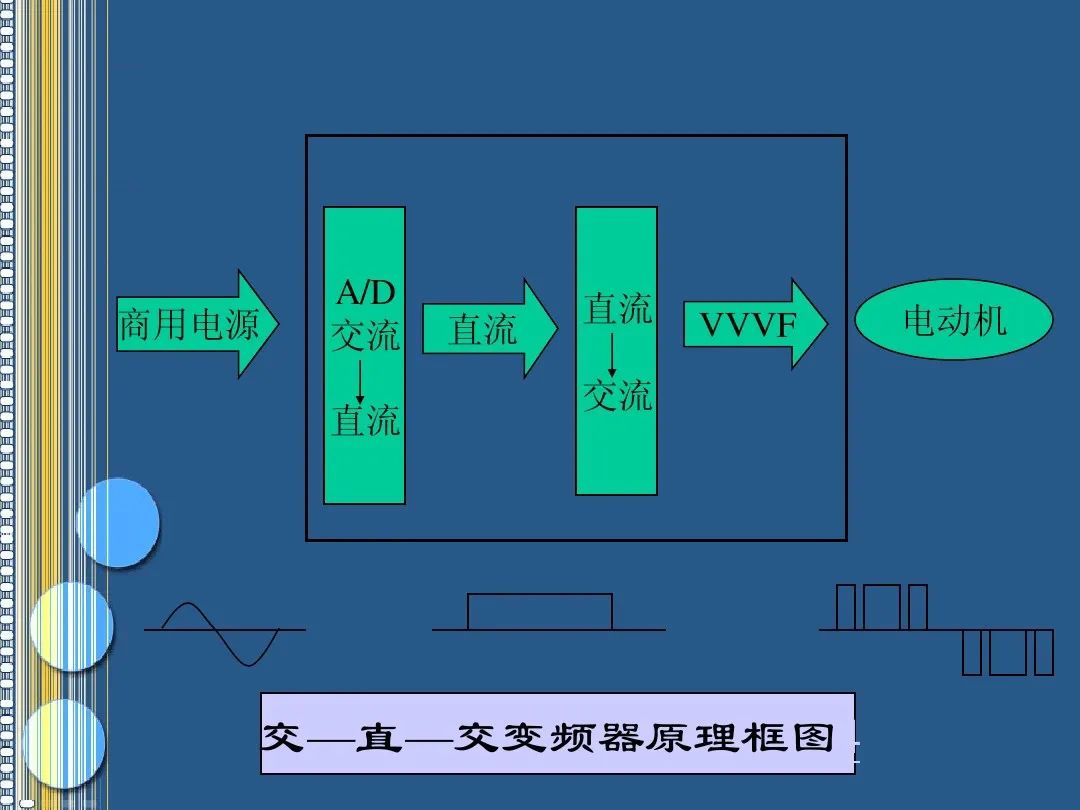
变频器的工作原理和功能应用
随机推荐
零基础学习CANoe Panel(3)—— 静态控件(Static Text , Group Box ,Picture Box)
LoRa无线技术与LoRaWAN网关模块的区别
爬虫与反爬:一场无休止之战
Five network IO models
1184. 公交站间的距离 : 简单模拟题
[FPGA]: IP core --divider (divider)
Zero basic learning canoe panel (7) -- file selection (pathdiaglog)
Analysis of Lagrange multiplier method and its duality
[interview: Basics 03: selection sort]
Golang Li Kou leetcode 494. goals and
CSDN blog removes the uploaded image watermark
[dish of learning notes dog learning C] advanced pointer
js树形结构,根据里层id找出它所属的每层父级集合
[about Modelsim simulation] design and Simulation of 4-bit counter
Distributed transaction processing scheme big PK!
简单使用 MySQL 索引
Hongmeng's first note
PIP update command
BBR and queuing
Zero basic learning canoe panel (9) -- combobox