当前位置:网站首页>NowCoderTOP35-40——持续更新ing
NowCoderTOP35-40——持续更新ing
2022-08-05 09:42:00 【王嘻嘻-】
TOP35. 判断是不是完全二叉树
public class Solution {
/** * 判断完全二叉树,当遍历当前层时如果遇到空节点,如果该空节点右侧还有节点,说明该树 * 一定不是完全二叉树,直接返回false,遍历完返回true * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * @param root TreeNode类 * @return bool布尔型 */
public boolean isCompleteTree (TreeNode root) {
// 空树是完全二叉树
if(root == null) return true;
// 辅助队列
Queue<TreeNode> queue = new LinkedList<>();
// 先将根节点入队
queue.offer(root);
// 标记空节点
boolean flag = true;
while(!queue.isEmpty()) {
TreeNode cur = queue.poll();
if(cur == null) {
// 如果遇到某个节点为空,进行标记
flag = false;
}else {
// 遇到空节点直接返回false
if(flag == false) return false;
queue.offer(cur.left);
queue.offer(cur.right);
}
}
return true;
}
}
TOP36. 判断是不是平衡二叉树
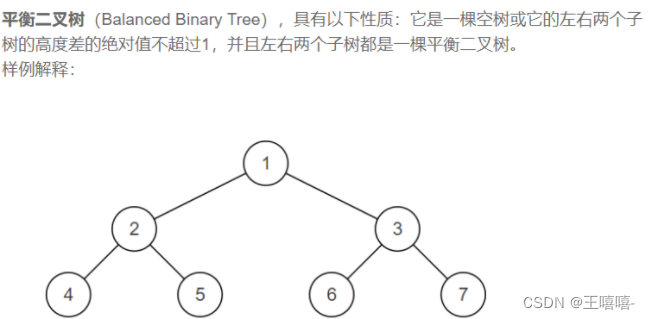
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
if(root == null) return true;
// 判断左子树和右子树是否符合规则,且深度不能超过2
return IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right)
&& Math.abs(TreeDepth(root.left) - TreeDepth(root.right)) <= 1;
}
// 二叉树的深度
public int TreeDepth(TreeNode root) {
if(root == null) return 0;
return Math.max(TreeDepth(root.left), TreeDepth(root.right)) + 1;
}
}
TOP37. 二叉搜索树的最近公共祖先
public class Solution {
/** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * @param root TreeNode类 * @param p int整型 * @param q int整型 * @return int整型 */
public int lowestCommonAncestor (TreeNode root, int p, int q) {
// 递归
// 空树没有最近公共祖先
if(root == null) return -1;
// pq在该节点两边说明这就是最近公共祖先
if(p >= root.val && q <= root.val || (q >= root.val && p <= root.val)){
return root.val;
}
//pq都在该节点的左边
else if(p <= root.val && q <= root.val) {
// 进入左子树
return lowestCommonAncestor(root.left, p , q);
}
else
// 进入右子树
return lowestCommonAncestor(root.right, p , q);
}
// 非递归
// // 从根节点到两个节点的路径
// ArrayList<Integer> listP = getPath(root, p);
// ArrayList<Integer> listQ = getPath(root, q);
// int res = 0;
// // 比较两个路径,找到第一个不同的点
// for(int i = 0; i < listP.size() && i < listQ.size(); i++) {
// int p1 = listP.get(i);
// int q1 = listQ.get(i);
// // 最后一个相同的节点就是最近公共祖先
// if(p1 == q1) res = p1;
// }
// return res;
// }
//
// // 求根节点到目标节点的路径
// public ArrayList<Integer> getPath(TreeNode root, int target) {
// ArrayList<Integer> list = new ArrayList<Integer>();
// TreeNode node = root;
// // 节点值不同,可以直接用值比较
// while(node.val != target) {
// list.add(node.val);
// if(target > node.val) node = node.right;
// else node = node.left;
// }
// // 将节点值加入链表
// list.add(node.val);
// return list;
// }
}
TOP38. 在二叉树中找到两个节点的最近公共祖先
public class Solution {
public int lowestCommonAncestor (TreeNode root, int o1, int o2) {
// 递归法
if(root == null) return -1;
// 该节点是其中某一个的节点时
if(root.val == o1 || root.val == o2) return root.val;
// 左子树中寻找公共祖先
int l = lowestCommonAncestor(root.left, o1, o2);
// 右子树中寻找
int r = lowestCommonAncestor(root.right, o1, o2);
// 左子树中未找到
if(l == -1) return r;
// 右子树中未找到
if(r == -1) return l;
// 否则返回当前节点
return root.val;
}
// step 1:利用dfs求得根节点到两个目标节点的路径:每次选择二叉树的一棵子树往下找,同时路径数组增加这个遍历的节点值。
// step 2:一旦遍历到了叶子节点也没有,则回溯到父节点,寻找其他路径,回溯时要去掉数组中刚刚加入的元素。
// step 3:然后遍历两条路径数组,依次比较元素值。
// step 4:找到两条路径第一个不相同的节点即是最近公共祖先。
// ArrayList<Integer> path1 = new ArrayList<Integer>();
// ArrayList<Integer> path2 = new ArrayList<Integer>();
// // 根节点到两个节点的路径
// dfs(root, path1, o1);
// // 重置标志位
// flag = false;
// // 查找下一个
// dfs(root, path2, o2);
// int res = 0;
// //比较两个路径,找到第一个不同的点
// for(int i = 0; i < path1.size() && i < path2.size(); i++) {
// int p1 = path1.get(i);
// int p2 = path2.get(i);
// if(p1 == p2) res = p1;
// else break;
// }
// return res;
// }
// // 记录是否找到到o的路径
// boolean flag = false;
// // 根节点到目标节点的路径
// public void dfs(TreeNode root, ArrayList<Integer> path, int o) {
// if(flag || root == null) return;
// // 根节点记录下
// path.add(root.val);
// // 节点值不同,so可以用值比较
// if(root.val == o) {
// flag = true;
// return;
// }
// // dfs遍历
// dfs(root.left, path, o);
// dfs(root.right, path, o);
// // 找到
// if(flag) return;
// // 没有找到,回溯
// path.remove(path.size() - 1);
// }
}
TOP40. 重建二叉树
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] vin) {
int lenPre = pre.length;
int lenIn = vin.length;
// 边界
if(lenPre == 0 || lenIn == 0) return null;
// 构建根节点
TreeNode root = new TreeNode(pre[0]);
for(int i = 0; i < lenIn ; i++) {
// 找到中序遍历的前序第一个元素
if(pre[0] == vin[i]) {
// 构建左子树
// Arrays.copyOfRange 数组中指定范围copy from to(不包括to)
root.left = reConstructBinaryTree(Arrays.copyOfRange(pre, 1, i + 1),
Arrays.copyOfRange(vin, 0, i));
//构建右子树
root.right = reConstructBinaryTree(Arrays.copyOfRange(pre, i + 1, pre.length),
Arrays.copyOfRange(vin, i + 1, vin.length));
break;
}
}
return root;
}
}
边栏推荐
- 15.1.1、md—md的基础语法,快速的写文本备忘录
- Open Source Summer | How OpenHarmony Query Device Type (eTS)
- Does flink cdc support synchronization from oracle dg library?
- 蚁剑webshell动态加密连接分析与实践
- leetcode: 529. Minesweeper Game
- Concurrent CAS
- 歌词整理
- 只有一台交换机,如何实现主从自动切换之nqa
- Overall design and implementation of Kubernetes-based microservice project
- dotnet OpenXML parsing PPT charts Getting started with area charts
猜你喜欢
皕杰报表的下拉框联动

七夕浪漫约会不加班,RPA机器人帮你搞定工作

Why do I recommend using smart async?

Oracle temporary table space role
CPU的亲缘性affinity

js 图形操作一(兼容pc、移动端实现 draggable属性 拖放效果)

Pytorch深度学习快速入门教程 -- 土堆教程笔记(三)

为什么我推荐使用智能化async?

Tanabata romantic date without overtime, RPA robot helps you get the job done
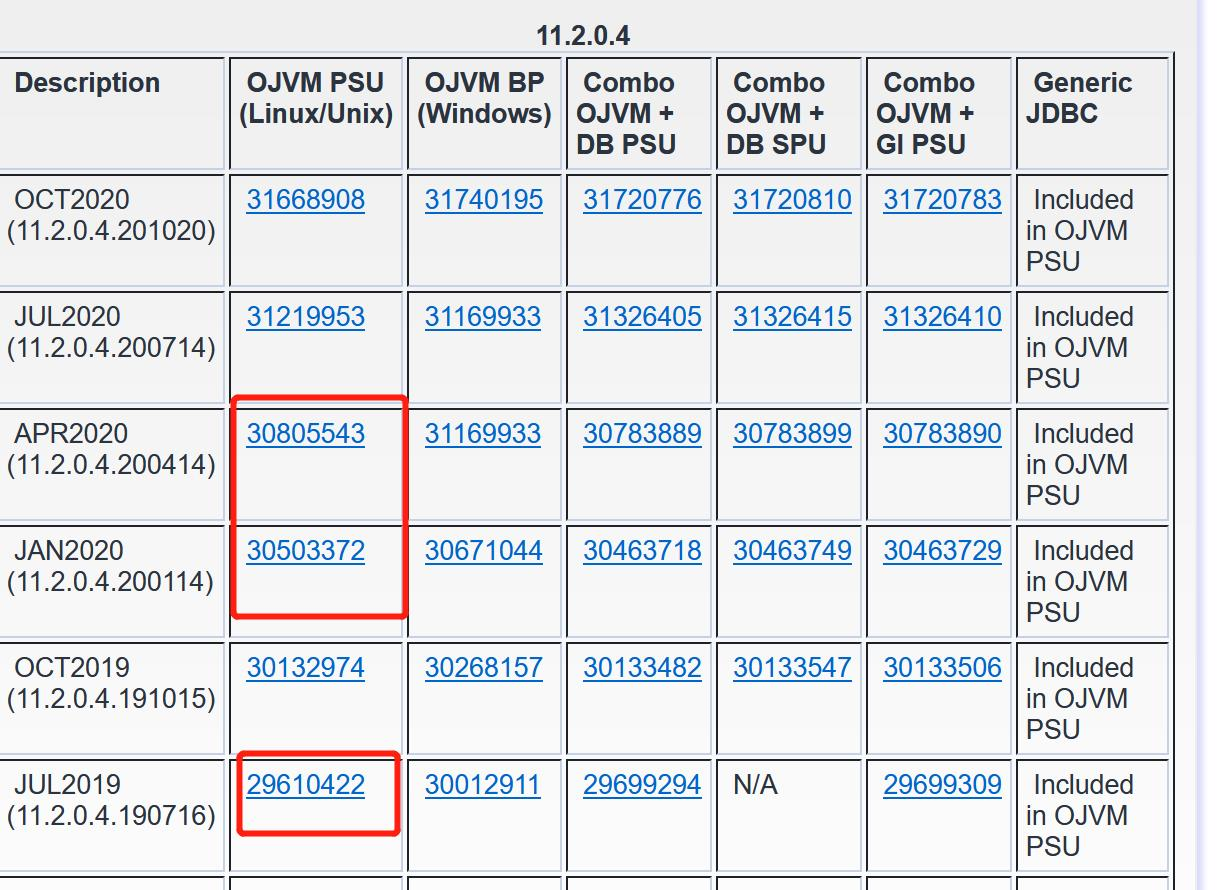
Which big guy has the 11G GI and ojvm patches in April or January 2020, please help?
随机推荐
C语言的高级用法
my journal link
无题十二
无题四
深度学习21天——卷积神经网络(CNN):服装图像分类(第3天)
Does flink cdc support synchronization from oracle dg library?
PAT Class B-B1019 Digital Black Hole (20)
【ASM】字节码操作 方法的初始化 Frame
Can MySQL use aggregate functions without GROUP BY?
明天去订票,准备回家咯~~
HStreamDB Newsletter 2022-07|分区模型优化、数据集成框架进一步完善
19.服务器端会话技术Session
Advanced usage of C language
基于 Kubernetes 的微服务项目整体设计与实现
eKuiper Newsletter 2022-07|v1.6.0:Flow 编排 + 更好用的 SQL,轻松表达业务逻辑
ECCV 2022 Oral Video Instance Segmentation New SOTA: SeqFormer & IDOL and CVPR 2022 Video Instance Segmentation Competition Champion Scheme...
【Excel实战】--图表联动demo_001
手把手教你纯c实现异常捕获try-catch组件
皕杰报表的下拉框联动
Creo 9.0 基准特征:基准点