当前位置:网站首页>OpenJudge NOI 2.1 1752:鸡兔同笼
OpenJudge NOI 2.1 1752:鸡兔同笼
2022-07-07 04:45:00 【君义_noip】
【题目链接】
【题目考点】
1. 枚举
【解题思路】
解法1:枚举
设有鸡x只,兔子y只,已知有a只脚,那么有
2 x + 4 y = a 2x+4y=a 2x+4y=a
鸡最少有0只,当所有的脚都是鸡脚时,鸡最多,有 a 2 \frac{a}{2} 2a只,所以 0 ≤ x ≤ a 2 0\le x \le \frac{a}{2} 0≤x≤2a
兔子最少有0只,最多有 ⌊ a 4 ⌋ \lfloor \frac{a}{4} \rfloor ⌊4a⌋只,所以 0 ≤ y ≤ ⌊ a 4 ⌋ 0\le y \le \lfloor \frac{a}{4} \rfloor 0≤y≤⌊4a⌋
总结为:
- 枚举对象:x, y
- 枚举范围: 0 ≤ x ≤ a 2 0\le x \le \frac{a}{2} 0≤x≤2a, 0 ≤ y ≤ ⌊ a 4 ⌋ 0\le y \le \lfloor \frac{a}{4} \rfloor 0≤y≤⌊4a⌋
- 枚举条件: 2 x + 4 y = a 2x+4y=a 2x+4y=a
选择所有满足条件的x与y中,x+y的最大与最小值。
解法2:找规律
如果输入的脚的数量为奇数,那么没有满足要求的答案。
当有尽量多的鸡时,动物应该是最多的。当有尽量多的兔子时,动物应该是最少的。
鸡最多为 a 2 \frac{a}{2} 2a,那么动物最多为 a 2 \frac{a}{2} 2a
兔子最多为 ⌊ a 4 ⌋ \lfloor \frac{a}{4} \rfloor ⌊4a⌋,剩下 a % 4 a\%4 a%4只脚都是鸡,有 a % 4 2 \frac{a\%4}{2} 2a%4只,此时动物最少,有 ⌊ a 4 ⌋ + a % 4 2 \lfloor \frac{a}{4} \rfloor+\frac{a\%4}{2} ⌊4a⌋+2a%4只。
【题解代码】
解法1:枚举
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
int main()
{
int a, mx = 0, mn = INF;
cin >> a;
for(int x = 0; x <= a/2; ++x)
for(int y = 0; y <= a/4; ++y)
{
if(2*x+4*y == a)
{
//更新最大值与最小值
mx = max(mx, x+y);
mn = min(mn, x+y);
}
}
if(mx == 0 && mn == INF)//如果没有找到
cout << "0 0";
else
cout << mn << ' ' << mx;
return 0;
}
解法2:找规律
#include<bits/stdc++.h>
using namespace std;
int main()
{
int a;
cin >> a;
if(a % 2 == 1)
cout << "0 0";
else
cout << a/4+a%4/2 << ' ' << a/2;
return 0;
}
边栏推荐
- [UTCTF2020]file header
- Yugu p1020 missile interception (binary search)
- Pytest+allure+jenkins installation problem: pytest: error: unrecognized arguments: --alluredir
- 【数字IC验证快速入门】10、Verilog RTL设计必会的FIFO
- [OBS] win capture requires winrt
- Common validation comments
- 央视太暖心了,手把手教你写HR最喜欢的简历
- Cnopendata list data of Chinese colleges and Universities
- 2022年茶艺师(中级)考试试题及模拟考试
- 2022 tea master (intermediate) examination questions and mock examination
猜你喜欢
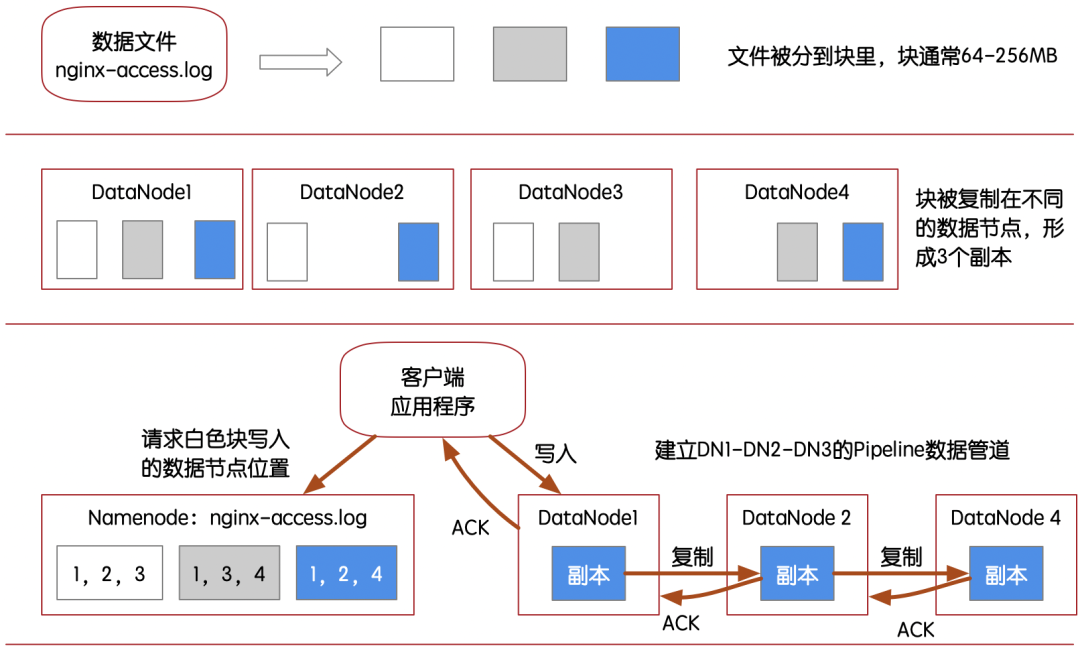
Explore Cassandra's decentralized distributed architecture
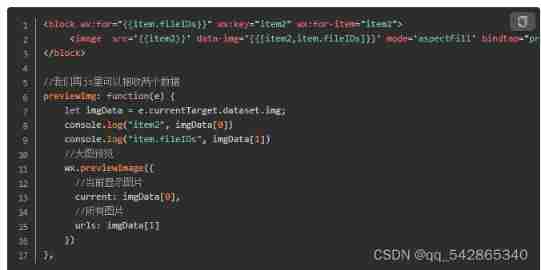
Wechat applet data binding multiple data
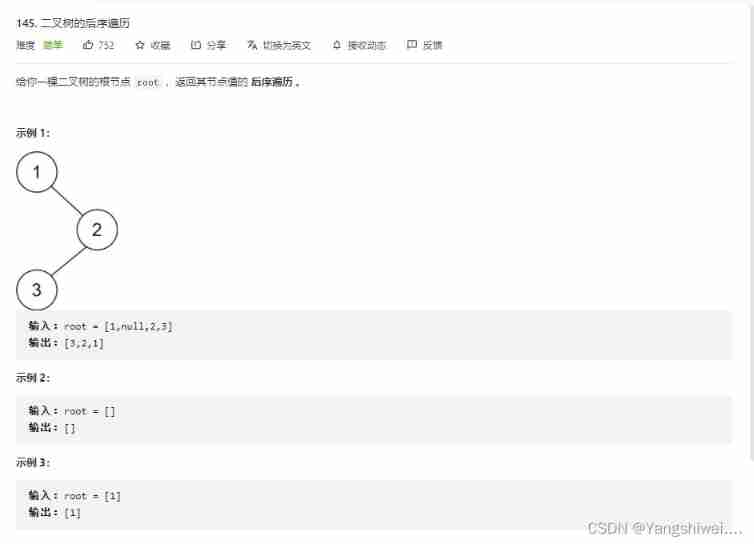
Force buckle 145 Binary Tree Postorder Traversal
numpy中dot函数使用与解析
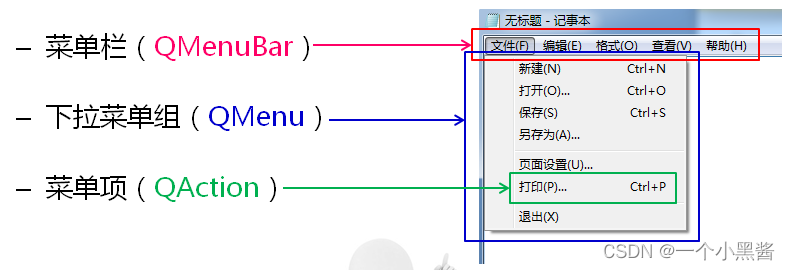
Main window in QT learning 27 application

即刻报名|飞桨黑客马拉松第三期等你挑战
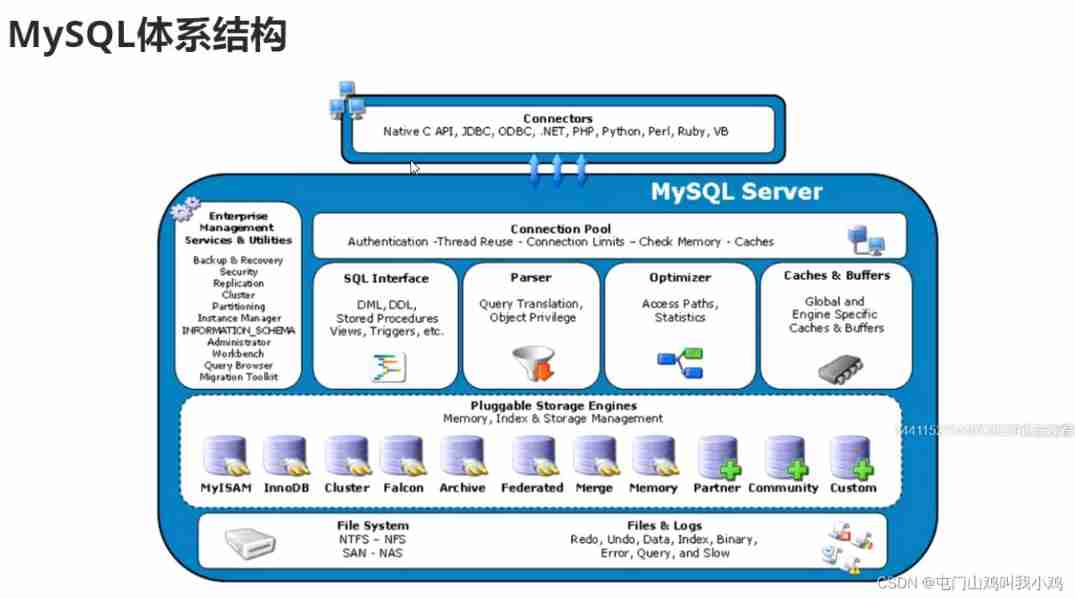
Linux server development, SQL statements, indexes, views, stored procedures, triggers
![[CV] Wu Enda machine learning course notes | Chapter 8](/img/c0/7a39355fb3a6cb506f0fbcf2a7aa24.jpg)
[CV] Wu Enda machine learning course notes | Chapter 8
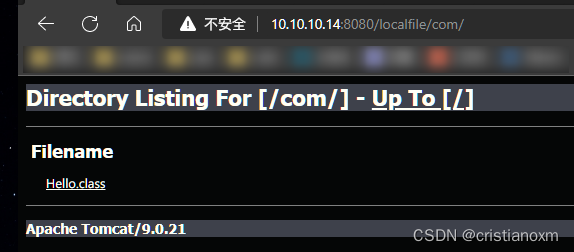
自定义类加载器加载网络Class
2022 tea master (intermediate) examination questions and mock examination
随机推荐
【数字IC验证快速入门】13、SystemVerilog interface 和 program 学习
The principle and implementation of buffer playback of large video files
[advanced digital IC Verification] command query method and common command interpretation of VCs tool
[webrtc] m98 Screen and Window Collection
[2022 actf] Web Topic recurrence
【数字IC验证快速入门】10、Verilog RTL设计必会的FIFO
numpy中dot函数使用与解析
Use and analysis of dot function in numpy
[UVM practice] Chapter 1: configuring the UVM environment (taking VCs as an example), run through the examples in the book
Who has docker to install MySQL locally?
C语言航班订票系统
Thinkcmf6.0 installation tutorial
[Stanford Jiwang cs144 project] lab4: tcpconnection
Linux server development, detailed explanation of redis related commands and their principles
CTF daily question day43 rsa5
2022 welder (elementary) judgment questions and online simulation examination
芯片 设计资料下载
Binary tree and heap building in C language
JSON data flattening pd json_ normalize
【数字IC验证快速入门】14、SystemVerilog学习之基本语法1(数组、队列、结构体、枚举、字符串...内含实践练习)