当前位置:网站首页>Basic Concepts of Graphs
Basic Concepts of Graphs
2022-08-03 22:04:00 【People live up to Qingshan】
图的基本概念
图的定义:
- 一个图是由点集V和边集E组成的,Generally recorded as G = <V,E>,An edge connects two vertices.
- 点集V中包含了所有的顶点,边集Econtains all edges,点集VWhen it is empty, it is called an empty graph.
- A graph consisting of all undirected edges is called an undirected graph,A graph consisting of directed edges is called a directed graph.The understanding of directed graph can be understood as a one-way street.
eg:
![[Pasted image 20220729172945.png]]
- 自环: 边连接的两个点是同一个点.
- 重边:An undirected graph has multiple edges between two points(>=2)连接,For a directed graph, there are multiple edges in the same direction between two points(>=2)连接.( Multiple edges in the same direction)
- 孤点 :A point without connected edges is called an orphan.(很少用)
- 简单图: A graph without self-loops and multiple edges is called a simple graph
度数:
- 无向图的度数 :For vertices in an undirected graphv,v作为边的端点的次数称为v的度数,记作d(v). The degree of a point is how many edges are connected to it
- 有向图的度数:For the vertices of a directed graphv,v作为边的起点的次数称为v的出度,记作d+(v);v作为边的终点的次数称为v的入度,记作d-(v);顶点v的度数d(v)=d+(v)+d-(v).
- 每个图GThe maximum degree of is the maximum of all fixed-point degrees,记作∆(G);最小度为所有顶点度数的最小值,记作δ(G).了解,一般不会用到
- 一张图GThe sum of the degrees of more points is twice the number of sides,The sum of out-degrees of all vertices in a directed graph is equal to the sum of in-degrees
完全图和竞赛图
- 完全图(无向图):设G为一个有n个节点的无向简单图,若G中每个顶点都与其余n-1 个顶点有边相连,则称G为n阶无向完全图,简称为 n阶完全图,记做Kn.
- 完全图(有向图):设G为一个有nA directed simple graph of nodes,若GEach vertex in is connected to the rest n-1 个顶点的边,And all these nodes are connected to his edge,则称G为n阶有向完全图
- 竞赛图:基于n阶无向完全图,给每条边任意确定一个方向形成的图称为n阶竞赛图.
> ![[Pasted image 20220729190107.png]]
子图、生成子图
- 子图: 设 G = <V,E>,G’ = <V’,E’> 为两个图(Both are undirected graphs or directed graphs),如果V’⊆ V且 E’ ⊆ E, 则称图G’ 为图G 的子图, G称为图G’的母图,记作 G’⊆ G.
- 如果V’ = V 或 E’ ⊂ E, 则称G’ 为 G的真子图
![[Pasted image 20220730105337.png]]
补图
- 补图 :设G=<V,E>是一个n阶无向简单图,以V为顶点集,以所有使G成为完全图KnA collection of edges that need to be added为边集的图,称为G的补图.
- The graph has the same set of vertices as its complement;Edge set vertex intersection is empty,A union is an edge set of a complete graph
- ![[Pasted image 20220730110346.png]]
同构
- 同构定义 :设G和G’是分别具有顶点集V和V’的两个图.如果存在一个双射(一一映射)h:V->V’,满足当且仅当(vi,vj)是G的边时,(h(vi),h(vj))是G’的边,则称G和G’同构
![[Pasted image 20220730110710.png]]
通路、回路、路径和距离
- 对于一个图 G,G 中顶点与边的交替序列v0e1v2e2v2——envn 称为v0到vn的通路,其中v0,vn称为通路的起点和终点,The number of edges in a path is called its长度.在有向图中,Keep the edges in the same direction.
- 对于一条通路,如果v0 = vn,则称为回路.如果v0 = vn 且其他所有顶点都不相同,则称为环.
- If all edges in the path are different,称为迹(All edges are passed only once).如果通路中的所有顶点都不相同,The sides also vary,则称为路径.(If both the point and the edge pass through once 叫做路径)‘
- Connect the two points in the figureShortest path length称为距离.
#### 连通性与连通块
- 无向图:
- 连通性 : 设无向图 G = <V,E>,u,v∈V,如果u,v之间存在通路,则称u,v是连通的.对于∀v∈V,v和v自己是连通的.
- 连通图 :对于任意非空无向图 G,若 G 中任意两个顶点都是连通的,则称 G 为连通图.
- 连通块 :对于无向图 G 的一个连通子图H,如果不存在 F 满足 H ⊂ F ⊆ G 且F 为连通图,则称 H 是 G 的一个连通块/连通分量,H 是一个极大连通子图.
- 有向图:
- 连通性:设有向图 G = <V,E>,u,v∈V,如果存在 u 到 v 的通路,则称 u 可达 v.如果u,v相互可达,则称为u,v 连通.
- 强连通: 如果有向图 G 中的顶点两两可达,则称G 为强连通图.
- 强连通块:Similar to undirected graphs,Directed graphs can be defined强连通/强连通分量.
图的存储——邻接矩阵
- 无向图的邻接矩阵 A : in a simple diagram,如果顶点 u 和顶点 v 之间存在一条边,则A[u][v] =A[v][u] = 1;如果没有则 A[u][v] = A[v][u] = 0. For the case with heavy edges,如果顶点 u 和 顶点 v 之间存在 k 条边
- 对于有向图,If there is a vertexu 到顶点v 的边,则A[u][v]在原来的基础上加一.
![[Pasted image 20220730164122.png]]
- 0 1 1 0 1 1 0 1 1 0 1 1 0 0 0 0 1 0 0 1 1 0 0 1 0 \begin{matrix} 0&1&1&0&1\\ 1&0&1&1&0\\ 1&1&0&0&0\\ 0&1&0&0&1\\ 1&0&0&1&0\\ \end{matrix} 0 1 1 0 1 10110110000100110010
### 邻接表 - 邻接表:When the number of nodes in a graph is relatively large,When using the adjacency matrix to store too much space,We will take the form of an adjacency list.A linked list is attached to each node,Stores edges or points that can be reached from this node.
边栏推荐
- 易基因|RNA m5C甲基化测序(RNA-BS)技术介绍
- 【kali-漏洞扫描】(2.1)Nessus下载安装(上)
- 三年黑盒测试工程师对嵌入式软件测试的理解
- 【进阶自动化测试】一文1000教你如何用Postman做接口自动化测试
- Shell编程的条件语句
- CAS:1260586-88-6_生物素-C5-叠氮_Biotin-C5-Azide
- CAS:1260586-88-6_Biotin-C5-Azide_Biotin-C5-Azide
- FVCOM 3D Numerical Simulation of Hydrodynamics, Water Exchange, Dispersion and Transport of Oil Spills丨FVCOM Model Watershed, Numerical Simulation Method of Marine Water Environment
- 1 秒完成授权,Authing 全新上线一键登录功能
- IDaaS 是什么?一文说清它的价值
猜你喜欢

《强化学习周刊》第56期:GraphIRL、REDEEMER & 眼科强化学习的潜在研究

XSS holes emersion

CAS: 773888-45-2_BIOTIN ALKYNE_Biotin-alkynyl
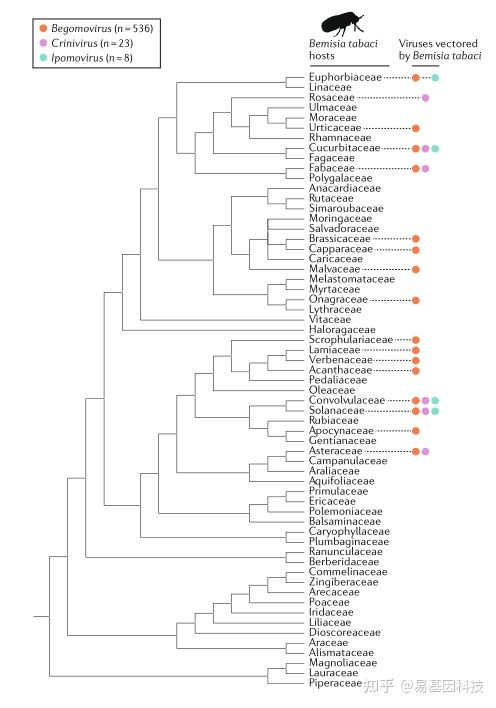
易基因:植物宏病毒组研究:植物病毒的进化与生态 | 顶刊综述
E-commerce data warehouse ODS layer-----log data loading
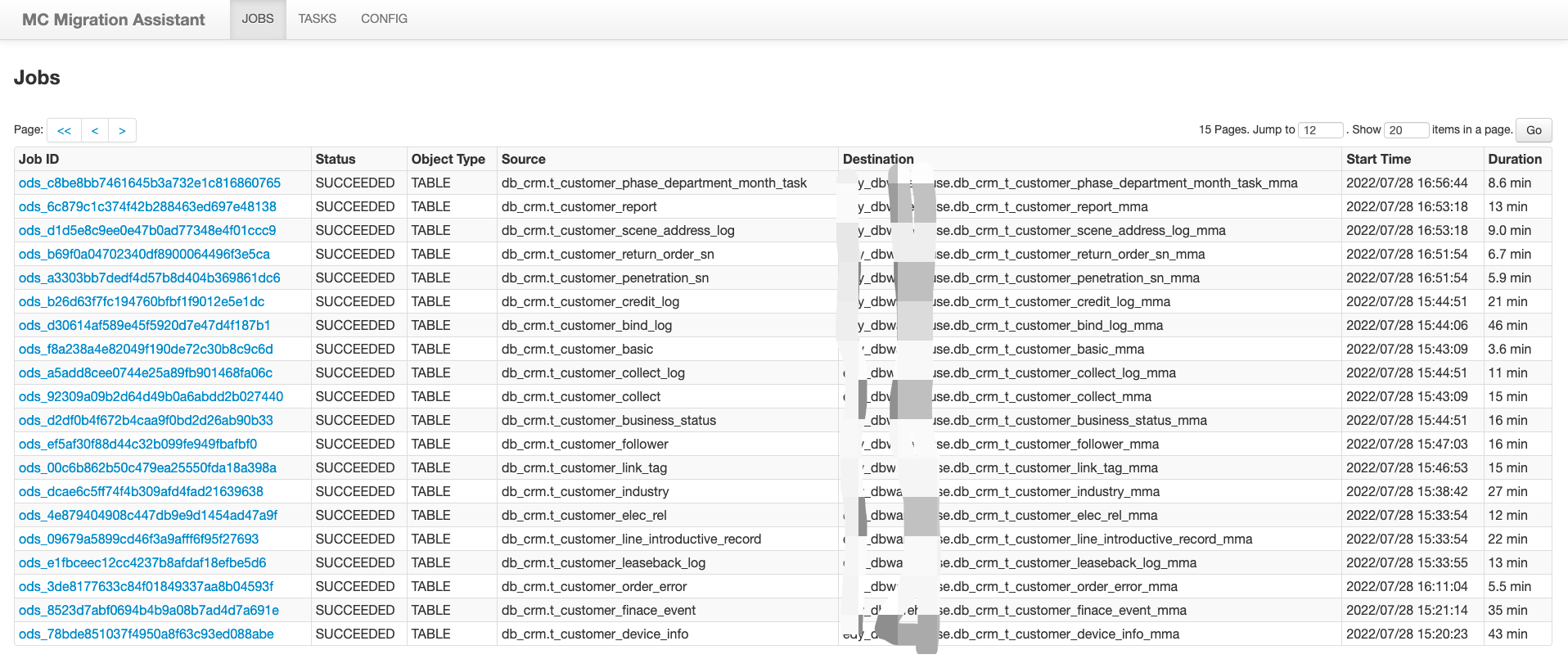
MMA安装及使用优化

剑指 Offer 16. 数值的整数次方

距LiveVideoStackCon 2022 上海站开幕还有3天!

HCIP第十六天
2022年全国职业院校技能大赛网络安全 B模块 B-1任务一:主机发现与信息收集 国赛原题
随机推荐
如何基于WPF写一款数据库文档管理工具(二)
CAS:153162-70-0_N-BOC-6-Biotinamidohexylamine
HCIP第十四天
Go开发工具GoLand V2022.2 来了——Go 工作区重大升级
[b01lers2020]Life on Mars
XSS holes emersion
超级实用网站+公众号合集
466. Count The Repetitions
从0到1看支付
dataframe multi-level index replace index df.swaplevel(axis=1)
What is the role and difference between buildscript and allprojects?
C. awoo‘s Favorite Problem--Educational Codeforces Round 130 (Rated for Div. 2)
上课笔记(6)(1)——#629. 表达式括号匹配(stack)
template string
1 秒完成授权,Authing 全新上线一键登录功能
C. Array Elimination-- Codeforces Round #751 (Div. 2)
HCIP第十五天
CAS:122567-66-2_DSPE-Biotin_DSPE-Biotin
『百日百题 · 基础篇』备战面试,坚持刷题 第四话——循环语句!
Cisco ike2 IPSec配置