当前位置:网站首页>Tree Chain Segmentation-
Tree Chain Segmentation-
2022-08-02 02:46:00 【xingxg.】
目录
LCA
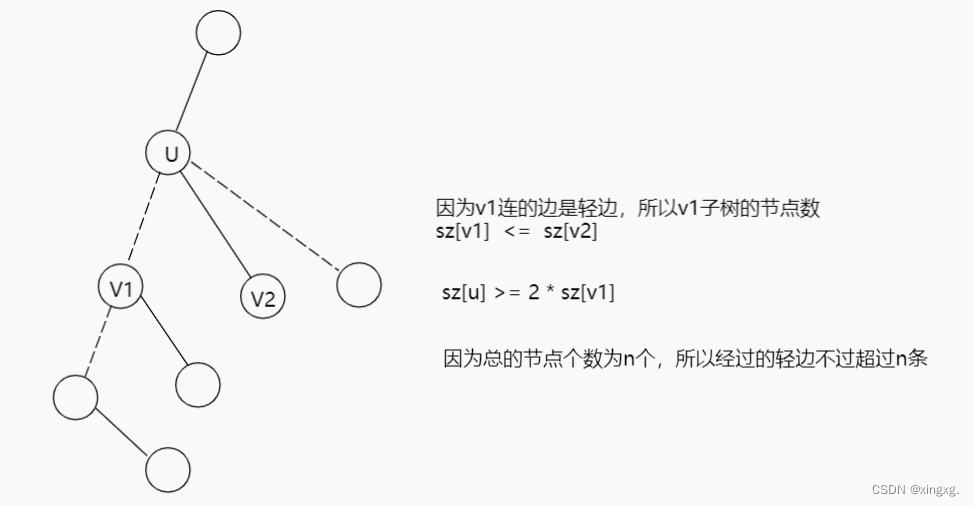
LCA问题,Can be solved using the previous multiplier,This can also be handled by tree chain segmentation.
Tree-chain splits are also commonly referred to as heavy-chain splits(无特殊说明).The other is long-chain splitting.Heavy chain dissection is the same as the definition of heavy son,It is also the largest number of nodes.
Every node will have a heavy edge(That is, find a subtree with the largest number of nodes among the children.)These heavy edges form a heavy chain.
The characteristics of tree chain segmentation:
A heavy chain is attached to each point,Probably the length of this heavy chain is only1,Maybe this point is the tip of the heavy chain. a heavy chain —— a light chain —— a heavy chain —— a light chain —— a heavy chain ...
// problem :
#include <bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> PII;
#define pb push_back
const int N = 101000;
int sz[N], hs[N], fa[N], dep[N], id[N], l[N], r[N], top[N];
std::vector<int> e[N];
int tot, n, m;
void dfs1(int u, int f) {
sz[u] = 1;
hs[u] = -1;
fa[u] = f;
dep[u] = dep[f] + 1;
for (auto v : e[u]) {
if (v == f) continue;
dfs1(v, u);
sz[u] += sz[v];
if (hs[u] == -1 || sz[hs[u]] < sz[v])
hs[u] = v;
}
}
void dfs2(int u, int t) {
top[u] = t;
// l[u] = ++tot;
// id[tot] = u;
if (hs[u] != -1) {
dfs2(hs[u], t);
}
for (auto v : e[u]) {
if (v != fa[u] && v != hs[u])
dfs2(v, v);
}
// r[u] = tot;
}
int LCA(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) v = fa[top[v]];
else u = fa[top[u]];
}
if (dep[u] < dep[v]) return u;
else return v;
}
int main(){
scanf("%d", &n);
for (int i = 1; i < n; ++i) {
int u, v;
scanf("%d %d", &u, &v);
e[u].push_back(v);
e[v].push_back(u);
}
dfs1(1, 0);
dfs2(1, 1);
scanf("%d", &m);
for (int i = 1; i <= m; ++i) {
int u, v;
scanf("%d %d", &u, &v);
printf("%d\n", LCA(u, v));
}
return 0;
}树的统计

Split the tree chain、Segment trees are joined together.模板题. 树链剖分 + DFS序(Prefer to traverse heavy edges,Make the sequence numbers of the multiple edges consecutive),在DFSon a sequential basis,建线段树.
要清楚DFS序中 l、r数组代表的含义,以及idxWhat the array represents.
idx[i] , 第i个DFSThe corresponding node number of the sequence,The initial value is used when building a line segment tree.
l[u] : u 节点对应的DFSthe left interval of the sequence,同时也是第l[u]traversed to the point
// problem :
#include <bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> PII;
#define pb push_back
const int N = 101000;
int n, m, a[N]; // 读入
std::vector<int> e[N]; // 读入
int sz[N], hs[N], fa[N], dep[N], top[N]; // 树链剖分
int l[N], r[N], tot, idx[N]; // DFS序
void dfs1(int u, int f) {
sz[u] = 1;
hs[u] = -1;
fa[u] = f;
dep[u] = dep[f] + 1;
for (auto v : e[u]) {
if (v == f) continue;
dfs1(v, u);
sz[u] += sz[v];
if (hs[u] == -1 || sz[hs[u]] < sz[v])
hs[u] = v;
}
}
void dfs2(int u, int t) {
top[u] = t;
l[u] = ++tot;
idx[tot] = u;
if (hs[u] != -1) {
dfs2(hs[u], t);
}
for (auto v : e[u]) {
if (v != fa[u] && v != hs[u])
dfs2(v, v);
}
r[u] = tot;
}
struct info {
int maxv, sum;
};
info operator + (const info &l, const info &r) {
info ans;
ans.maxv = max(l.maxv, r.maxv);
ans.sum = l.sum + r.sum;
return ans;
}
struct node {
info val;
}seg[N * 4];
void update(int id) {
seg[id].val = seg[id * 2].val + seg[id * 2 + 1].val;
}
void build(int id, int l, int r){ // 基于DFS序建线段树,不是节点1-n
if(l == r) {
// L号点,DFS序中的第L个点
seg[id].val = {a[idx[l]], a[idx[l]]};
} else {
int mid = (l + r) / 2;
build(id * 2, l, mid);
build(id * 2 + 1, mid + 1, r);
update(id);
}
}
void change(int id, int l, int r, int pos, int val) {
if(l == r) {
seg[id].val = {val, val};
} else {
int mid = (l + r) / 2;
if(pos <= mid) change(id * 2, l, mid, pos, val);
else change(id * 2 + 1, mid + 1, r, pos, val);
update(id);
}
}
info query(int id, int l, int r, int ql, int qr) {
if(ql == l && qr == r) {
return seg[id].val;
}
int mid = (l + r) / 2;
if(qr <= mid) return query(id * 2, l, mid, ql, qr);
else if(ql > mid) return query(id * 2 + 1, mid + 1, r, ql, qr);
else return query(id * 2, l, mid, ql, mid) +
query(id * 2 + 1, mid + 1, r, mid + 1, qr);
}
info query(int u, int v) {
info ans {(int) -1e9, 0};
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) {
ans = ans + query(1, 1, n, l[top[v]], l[v]);
v = fa[top[v]];
} else {
ans = ans + query(1, 1, n, l[top[u]], l[u]);
u = fa[top[u]];
}
}
if (dep[u] <= dep[v]) ans = ans + query(1, 1, n, l[u], l[v]);
else ans = ans + query(1, 1, n, l[v], l[u]);
return ans;
}
int main(){
scanf("%d", &n);
for (int i = 1; i < n; ++i) {
int u, v;
scanf("%d %d", &u, &v);
e[u].push_back(v);
e[v].push_back(u);
}
for (int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
dfs1(1, 0);
dfs2(1, 1);
build(1, 1, n);
scanf("%d", &m);
for (int i = 1; i <= m; ++i) {
int u, v;
static char op[10];
scanf("%s%d %d", op, &u, &v);
if (op[0] == 'C') {
change(1, 1, n, l[u], v);
} else {
info ans = query(u, v);
if (op[1] == 'M') printf("%d\n", ans.maxv);
else printf("%d\n", ans.sum);
}
}
return 0;
}边栏推荐
- feign调用不通问题,JSON parse error Illegal character ((CTRL-CHAR, code 31)) only regular white space (r
- Oracle19c安装图文教程
- aws s3 upload file
- 罗德里格斯公式(Rodrigues‘ Rotation Formula)推导
- AcWing 1285. Word Problem Solving (AC Automata)
- [Unity entry plan] 2D Game Kit: A preliminary understanding of the composition of 2D games
- OperatingSystemMXBean获取系统性能指标
- analog IC layout-Environmental noise
- Chrome浏览器无法加载已解压的.crx文件的解决办法
- 通用客户端架构
猜你喜欢

2022牛客多校四_G M
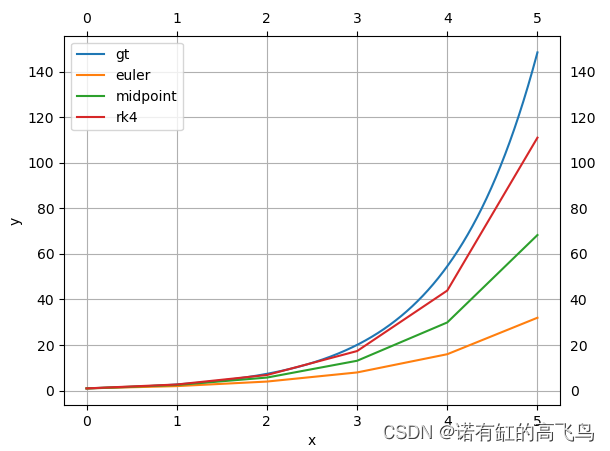
数值积分方法:欧拉积分、中点积分和龙格-库塔法积分

树链剖分-
Entry name 'org/apache/commons/codec/language/bm/gen_approx_greeklatin.txt' collided

Unable to log in to the Westward Journey
Nacos源码分析专题(一)-环境准备

项目场景 with ERRTYPE = cudaError CUDA failure 999 unknown error

analog IC layout-Parasitic effects

CASE2023

Install mysql using docker
随机推荐
很有意思的经历,很有意思的项目--文件夹对比工具
数仓:为什么说 ETL 的未来不是 ELT,而是 EL (T)
一次SQL优化,数据库查询速度提升 60 倍
Safety (2)
【Unity入门计划】2D Game Kit:初步了解2D游戏组成
Nanoprobes多组氨酸 (His-) 标签标记:重组蛋白检测方案
内卷的正确打开方式
Nanoprobes免疫测定丨FluoroNanogold试剂免疫染色方案
pyqt上手体验
数值积分方法:欧拉积分、中点积分和龙格-库塔法积分
789. 数的范围
Moonbeam and Project integration of the Galaxy, bring brand-new user experience for the community
欧拉公式的证明
Flask入门学习教程
240...循迹
Outsourcing worked for three years, it was abolished...
Chapter 7 Noise analysis
记一次gorm事务及调试解决mysql死锁
【web】理解 Cookie 和 Session 机制
(1) Redis: Key-Value based storage system