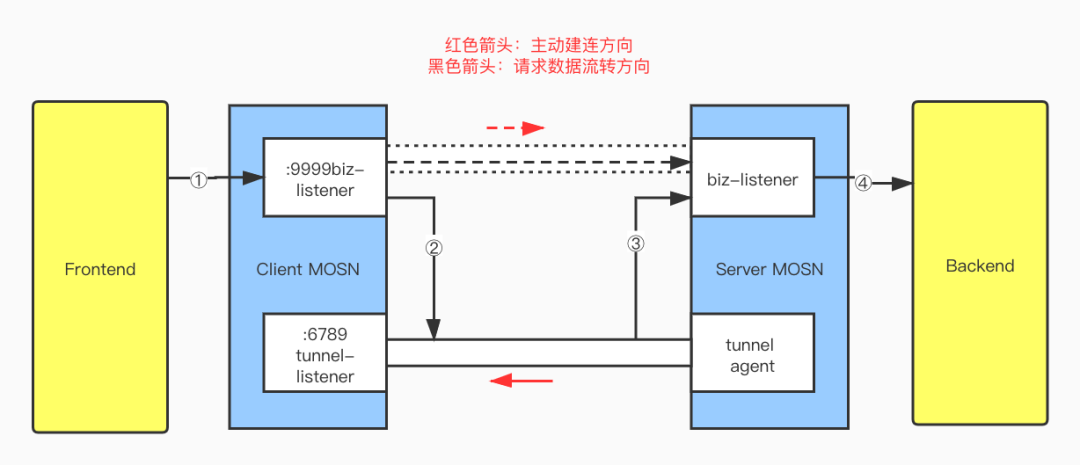
当前位置:网站首页>Leetcode刷题——单调栈问题(739每日温度问题、496下一个更大元素I、503下一个更大元素 II)
Leetcode刷题——单调栈问题(739每日温度问题、496下一个更大元素I、503下一个更大元素 II)
2022-08-02 19:23:00 【lonelyMangoo】
概述
写了单调栈的思路、使用,然后单调栈完成了Leetcode:739每日温度问题、496下一个更大元素I、503下一个更大元素 II。
为什么要用单调栈?
先看看这道题:每日温度
这道题拿到手没思路,直接上暴力,每个元素都到后面去找比自己大的,时间复杂度是O(n^2)
public int[] dailyTemperatures(int[] temperatures) {
int[] res = new int[temperatures.length];
int i,j;
for (i = 0; i < temperatures.length; i++) {
int today=temperatures[i];
for (j = i; j < temperatures.length; j++) {
if(temperatures[j]>today){
res[i]=j-i;
break;
}
}
}
return res;
}
然后翻了一翻评论,都在说用单调栈,于是去卡哥那里学习了一下。
那就回到我们一开始的问题,什么时候使用单调栈?
卡哥是这样写的:
通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。
说一下我的个人理解:遇到一维数组需要找比自己大或者小的元素的时候,我们一般都会用两个循环,在两个循环里进行优化,时间复杂度还是O(n^2),所以采用一种空间换时间的方法,就是单调栈。
什么是单调栈?
拿上面这道题而言,当我们用暴力时,实际上是对当前元素到后面去找比自己大的,但是可不可以换一个思路,把那些没找到比自己大的元素先保存下来,在找到比自己大的元素的时候,再取出来。我个人认为暴力相当于是饿加载,我出现的时候我就要找到比我大的,单调栈相当于是懒加载,我自己现在那儿呆着,比我大的元素出现的时候,我再出来表示我找到了比我大的元素。
首先我们要准备一个单调栈,栈中存的元素是数组下标(数组中的值能够通过下标获取),我下面说的元素是下标对应的值
单调栈的处理有三种情况
- 当前元素比栈头元素小,入栈
- 当前元素和栈头元素相等,入栈
- 当前元素比栈头元素大,把栈中比当前元素小的都找出来。将当前元素入栈。
以下面的数组为例:
数组:[74,75,71,69,72,76]
索引:[0,1,2,3,4,5]
1 第一个元素入栈
栈:|0
2 75比74大
所以栈中元素出栈,已经找到了最近的比自己大的,并将75入栈
栈:| 1
3 71 比75小
入栈
69比71小 入栈
栈:| 1 2 3
4 72比栈头的69大
69出栈,找到了对应的比自己大的
71也出栈,72也比自己大
由于72比75小,比较停止,72入栈
栈:|1 4
4. 76比 72 大 72出栈
76也比75大 75出栈
72和75都找到了比自己大的
76入栈
栈:|76
5 没有满足自己条件的元素了遍历结束
可能表达的不够清晰,如果有小伙伴看到这里,望见谅。
时间复杂度
循环里将数组所有元素取一遍,虽然循环里有while,但是while里是把栈的元素都取了一遍,栈中的实际上就是数组所有的元素取一遍。所以时间啊复杂度应该是O(n+n),也就是O(n)
用单调栈完成“每日温度”
直接上代码:
public static int[] dailyTemperatures1(int[] temperatures) {
Stack<Integer> stack = new Stack<>();
int[] res = new int[temperatures.length];
//降低一个元素入栈
stack.push(0);
for (int i = 1; i < temperatures.length; i++) {
//第一种和第二种情况,当前元素不比栈中元素大,入栈
if(temperatures[i]<= temperatures[stack.peek()]){
stack.push(i);
}else {
//这里有两个判断条件,栈空肯定是的,后面一个条件也必须满足,可以参考例子中75是怎么找到比自己大的元素的,因为我们的目标是找到比自己的大,而不是找栈里的!
while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]){
int top = stack.pop();
res[top] = i-top;
}
stack.push(i);
}
}
return res;
}
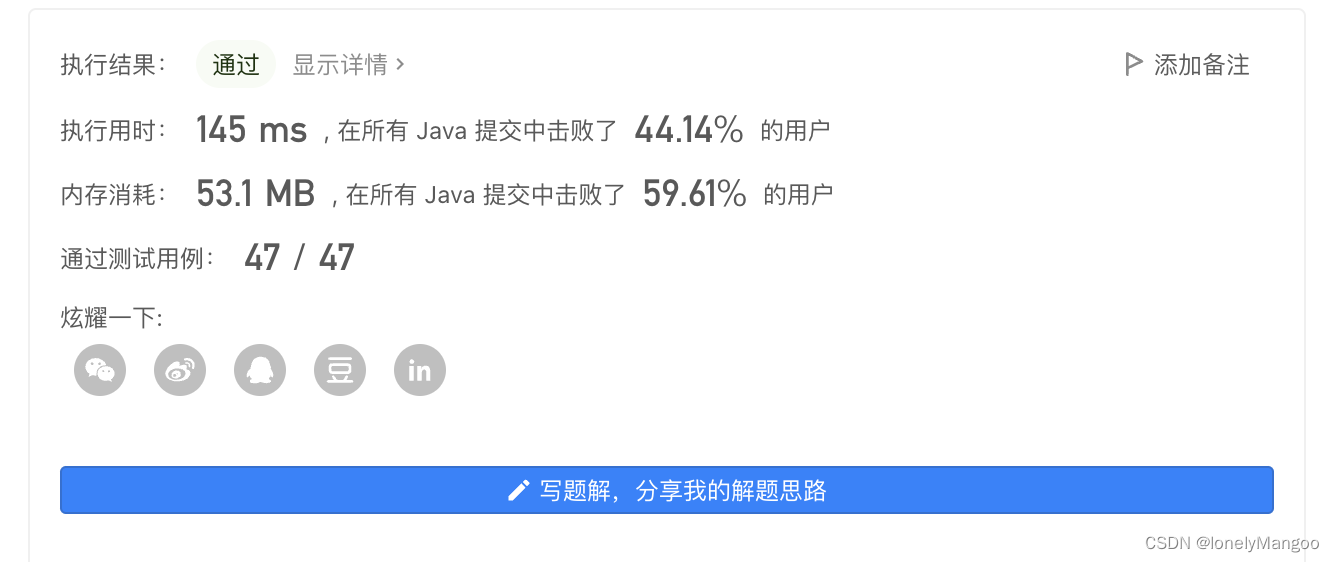
时间效率明显提高
以上代码比较冗余,可以将一二步合并,但是实际上一二步做的入栈工作,第三部也需要做,所以判断也可以省去没代码如下:
public static int[] dailyTemperatures2(int[] temperatures) {
Stack<Integer> stack = new Stack<>();
int[] res = new int[temperatures.length];
stack.push(0);
for (int i = 1; i < temperatures.length; i++) {
//每次记录的只是比前一个元素小的,可能出现比前一个元素大的一点,但是没有一开始的大的请款
while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
int top = stack.pop();
res[top] = i - top;
}
stack.push(i);
}
return res;
}
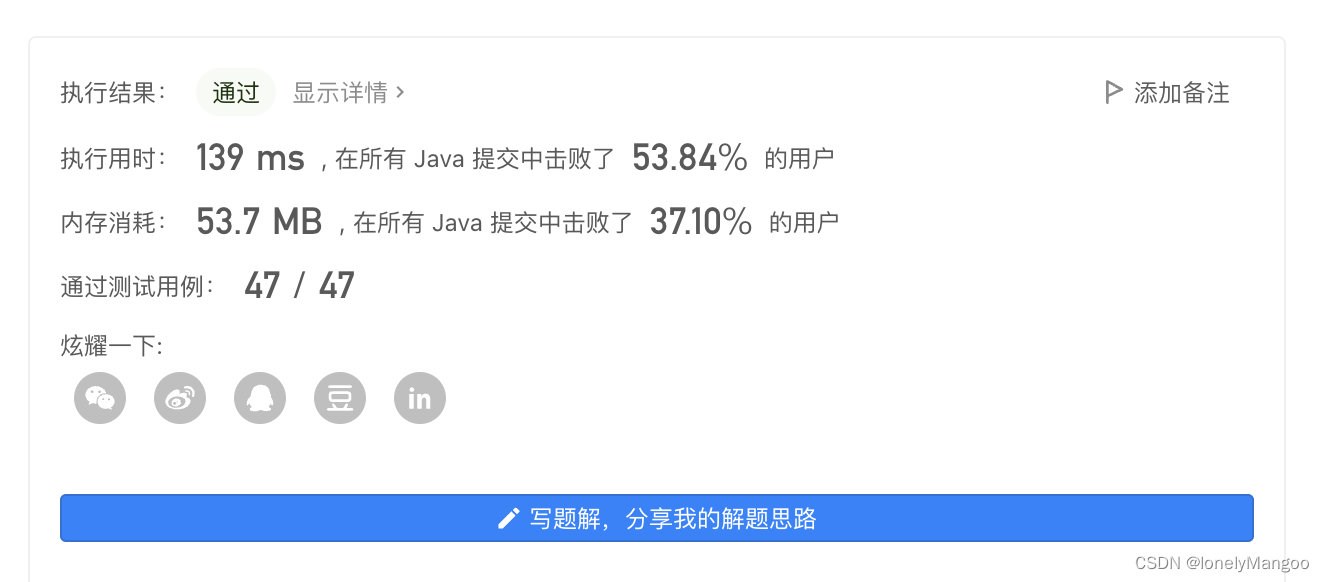
但是实际上这里的时间空间都不是很好,于是尝试吧Stack改成Deque
public int[] dailyTemperatures(int[] temperatures) {
Deque<Integer> stack = new LinkedList<>();
int[] res = new int[temperatures.length];
stack.push(0);
for (int i = 1; i < temperatures.length; i++) {
//每次记录的只是比前一个元素小的,可能出现比前一个元素大的一点,但是没有一开始的大的请款
while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
int top = stack.pop();
res[top] = i - top;
}
stack.push(i);
}
return res;
}
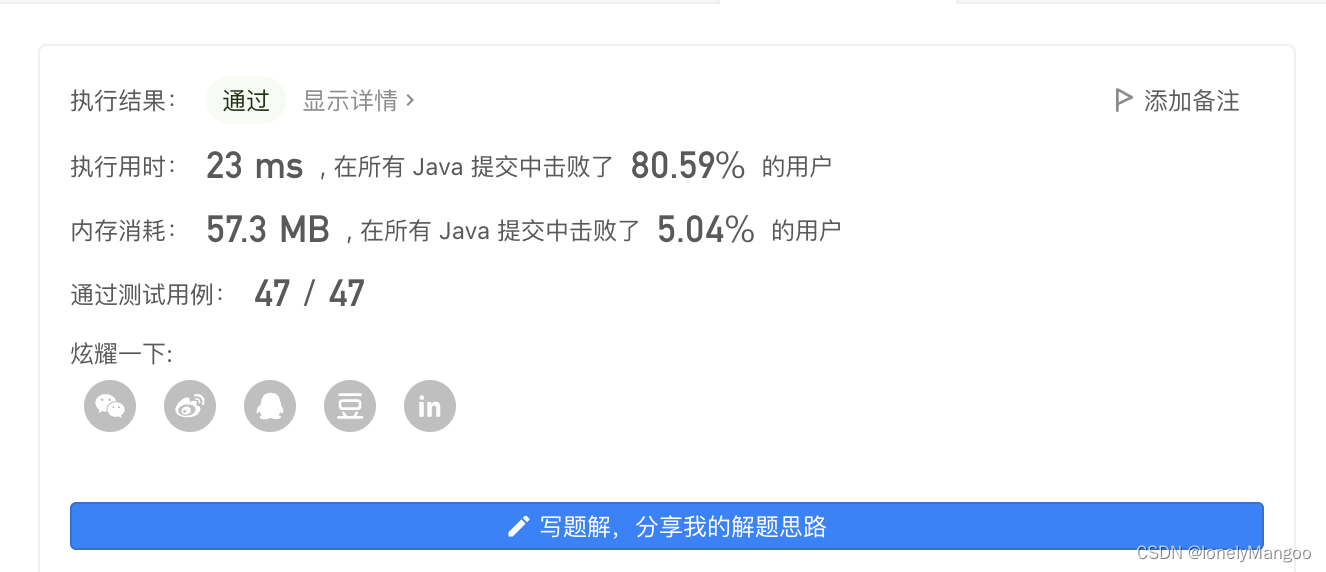
我觉得有必要去了解一下deque和stack的底层…
496下一个更大元素I
在了解完单调栈之后,下面两道就可以轻松解决,先看看这道题
496下一个更大元素I
题目说的天花乱坠,总结下来和之前的区别就是
- 从找下标变成了找值
- 要找多个值
所以这道题的思路,就是在大数组里找元素,然后记录下最大值,用一个map存储,需要哪个,到map中去找即可。
代码:
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
Map<Integer, Integer> map = new HashMap<>(nums2.length);
Stack<Integer> stack = new Stack<>();
//因为这里是无重复元素的,所以可以直接用
stack.push(0);
for (int i = 1; i < nums2.length; i++) {
if (nums2[i] > nums2[stack.peek()]) {
while (!stack.isEmpty() && nums2[i] > nums2[stack.peek()]) {
int top = stack.pop();
map.put(nums2[top], nums2[i]);
}
}
stack.push(i);
}
int[] res = new int[nums1.length];
for (int i = 0; i < nums1.length; i++) {
res[i] = map.getOrDefault(nums1[i], -1);
}
return res;
}
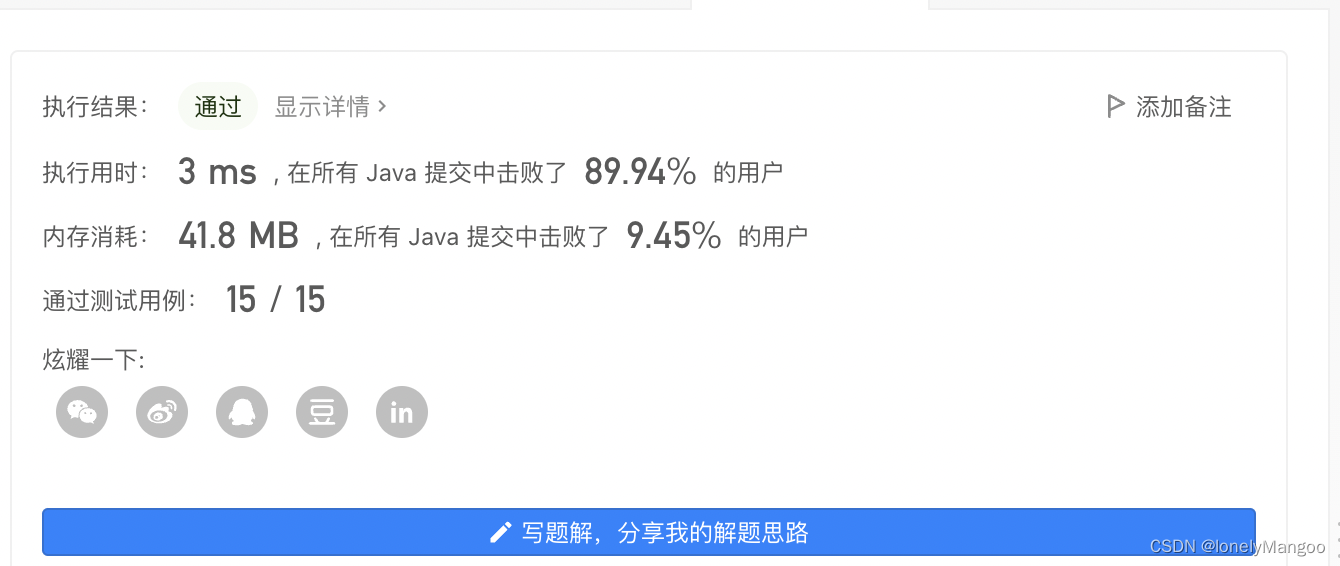
503下一个更大元素 II
503下一个更大元素 II
这道题和之前的区别不大了,我一开始就是想用取余做,但是调试老是出问题,就直接把数组变成原来的两倍。
public static int[] nextGreaterElements(int[] nums) {
int len = nums.length;
int[] nowNums = new int[len * 2];
int[] res = new int[nowNums.length];
for (int i = 0, j = len; i < len; i++, j++) {
nowNums[i] = nums[i];
nowNums[j] = nums[i];
res[i] = -1;
}
Stack<Integer> stack = new Stack<>();
stack.push(0);
for (int i = 1; i < nowNums.length; i++) {
if (nowNums[i] > nowNums[stack.peek()]) {
//每次记录的只是比前一个元素小的,可能出现比前一个元素大的一点,但是没有一开始的大的请款
while (!stack.isEmpty() && nowNums[i] > nowNums[stack.peek()]) {
int top = stack.pop();
res[top] = nowNums[i];
}
}
stack.push(i);
}
return Arrays.stream(res).limit(len).toArray();
}
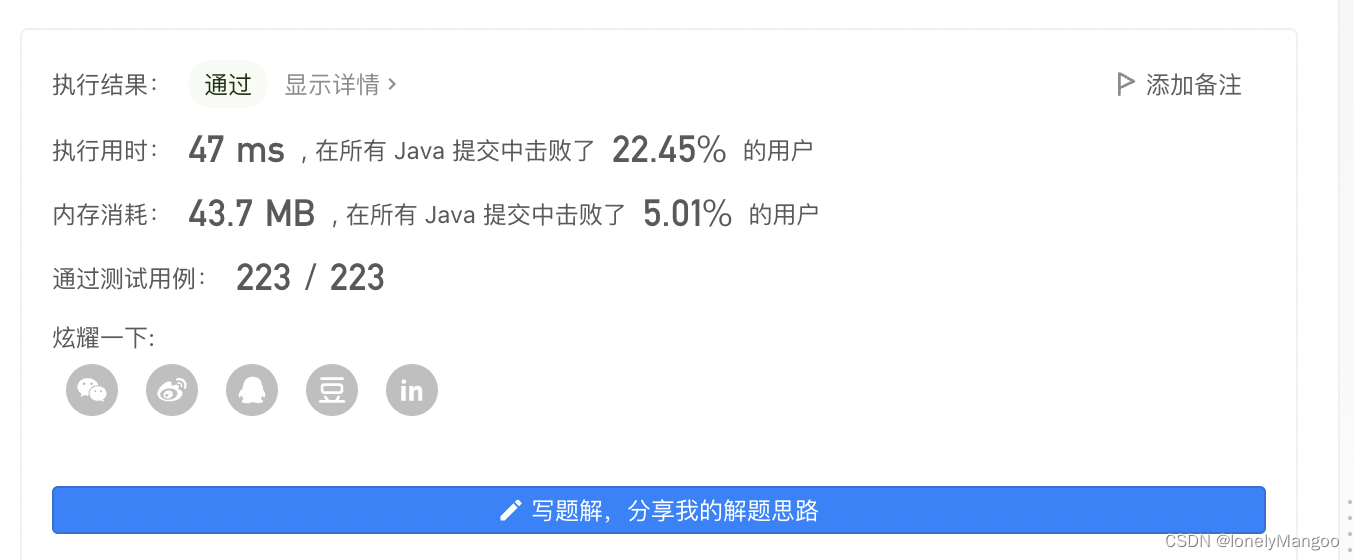
效率太差,试试取余,
public static int[] nextGreaterElements2(int[] nums) {
int len = nums.length;
int[] res = new int[len];
Stack<Integer> stack = new Stack<>();
Arrays.fill(res, -1);
stack.push(0);
for (int i = 1; i < len * 2; i++) {
//每次记录的只是比前一个元素小的,可能出现比前一个元素大的一点,但是没有一开始的大的请款
while (!stack.isEmpty() && nums[i % len] > nums[stack.peek() % len]) {
int top = stack.pop() ;
res[top % len] = nums[i % len];
}
stack.push(i);
}
return res;
}
这里不需要担心越界,因为所有数据都取余了。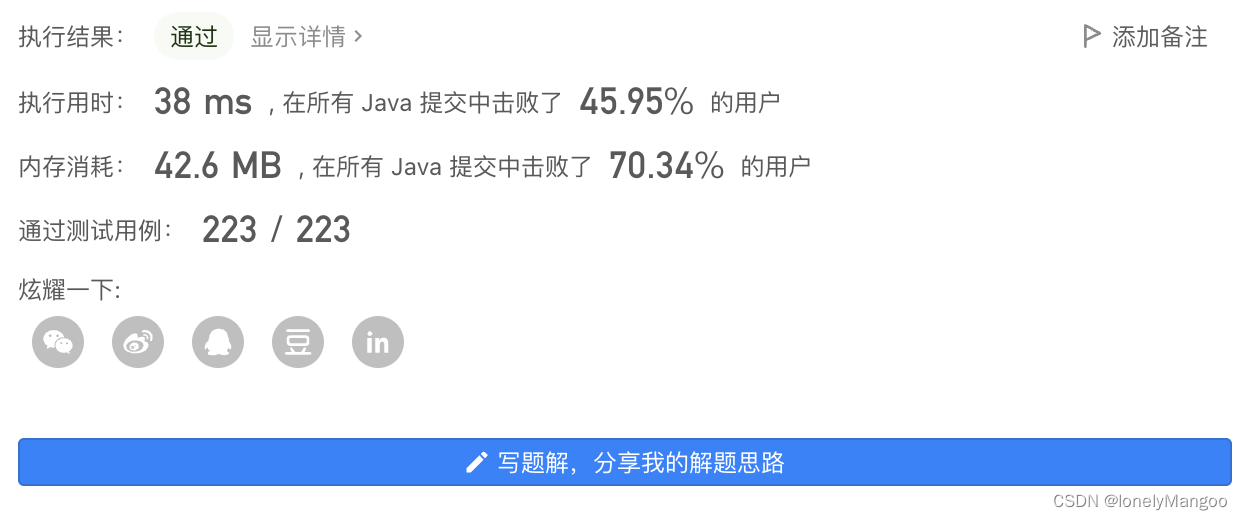
参考
边栏推荐
猜你喜欢
随机推荐
实现客户服务自助,打造产品知识库
VMware虚拟机无法上网
脑机接口003 | 马斯克称已实现与云端的虚拟自己对话,相关概念股份大涨
Therapy | How to Identify and Deal with Negative Thoughts
移动跨端技术方案分析对比
J9 digital theory: the Internet across chain bridge has what effect?
【LeetCode】118. 杨辉三角 - Go 语言题解
Go----Go 语言快速体验之开发环境搭建及第一个项目HelloWord
什么是现场服务管理系统(FSM)?有什么好处?
SQL server有什么认证吗?
磁盘分区的知识
元旦快乐(2022)
【软件工程导论】软件工程导论笔记
Office2021 安装MathType
聊一聊 AS 的一些好用的功能
当TIME_WAIT状态的TCP正常挥手,收到SYN后…
MaxCompute 近期发布上线的版本的 SQL 引擎新功能参数化视图有什么优势?
平稳发展 | 西欧地区手游玩家的数据和洞察
MySQL安装(详细,适合小白)
What is the use of IT assets management software