归并排序详解及应用

算法思路

就这么说吧，所有递归的算法，你甭管它是干什么的，本质上都是在遍历一棵（递归）树，然后在节点（前中后序位置）上执行代码，你要写递归算法，本质上就是要告诉每个节点需要做什么。

你看归并排序的代码框架:

// 定义：排序 nums[lo..hi]
void sort(int[] nums, int lo, int hi) {
    
    if (lo == hi) {
    
        return;
    }
    int mid = (lo + hi) / 2;
    // 利用定义，排序 nums[lo..mid]
    sort(nums, lo, mid);
    // 利用定义，排序 nums[mid+1..hi]
    sort(nums, mid + 1, hi);

    /****** 后序位置 ******/
    // 此时两部分子数组已经被排好序
    // 合并两个有序数组，使 nums[lo..hi] 有序
    merge(nums, lo, mid, hi);
    /*********************/
}

// 将有序数组 nums[lo..mid] 和有序数组 nums[mid+1..hi]
// 合并为有序数组 nums[lo..hi]
void merge(int[] nums, int lo, int mid, int hi);

看这个框架，也就明白那句经典的总结：归并排序就是先把左半边数组排好序，再把右半边数组排好序，然后把两半数组合并。

上述代码和二叉树的后序遍历很像：

/* 二叉树遍历框架 */
void traverse(TreeNode root) {
    
    if (root == null) {
    
        return;
    }
    traverse(root.left);
    traverse(root.right);
    /****** 后序位置 ******/
    print(root.val);
    /*********************/
}

前文 二叉树（纲领篇） 说二叉树问题可以分为两类思路，一类是遍历一遍二叉树的思路，另一类是分解问题的思路，根据上述类比，显然归并排序利用的是分解问题的思路

归并排序的过程可以在逻辑上抽象成一棵二叉树，树上的每个节点的值可以认为是 nums[lo..hi]，叶子节点的值就是数组中的单个元素：

然后，在每个节点的后序位置（左右子节点已经被排好序）的时候执行 merge 函数，合并两个子节点上的子数组：

代码实现及分析

《算法 4》中给出的归并排序代码兼具了简洁和高效的特点，所以我们可以参考书中给出的代码作为归并算法模板：

class Merge {
    

    // 用于辅助合并有序数组
    private static int[] temp;

    public static void sort(int[] nums) {
    
        // 先给辅助数组开辟内存空间
        temp = new int[nums.length];
        // 排序整个数组（原地修改）
        sort(nums, 0, nums.length - 1);
    }

    // 定义：将子数组 nums[lo..hi] 进行排序
    private static void sort(int[] nums, int lo, int hi) {
    
        if (lo == hi) {
    
            // 单个元素不用排序
            return;
        }
        // 这样写是为了防止溢出，效果等同于 (hi + lo) / 2
        int mid = lo + (hi - lo) / 2;
        // 先对左半部分数组 nums[lo..mid] 排序
        sort(nums, lo, mid);
        // 再对右半部分数组 nums[mid+1..hi] 排序
        sort(nums, mid + 1, hi);
        // 将两部分有序数组合并成一个有序数组
        merge(nums, lo, mid, hi);
    }

    // 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组
    private static void merge(int[] nums, int lo, int mid, int hi) {
    
        // 先把 nums[lo..hi] 复制到辅助数组中
        // 以便合并后的结果能够直接存入 nums
        for (int i = lo; i <= hi; i++) {
    
            temp[i] = nums[i];
        }

        // 数组双指针技巧，合并两个有序数组
        int i = lo, j = mid + 1;
        for (int p = lo; p <= hi; p++) {
    
            if (i == mid + 1) {
    
                // 左半边数组已全部被合并
                nums[p] = temp[j++];
            } else if (j == hi + 1) {
    
                // 右半边数组已全部被合并
                nums[p] = temp[i++];
            } else if (temp[i] > temp[j]) {
    
                nums[p] = temp[j++];
            } else {
    
                nums[p] = temp[i++];
            }
        }
    }
}

有了之前的铺垫，这里只需要着重讲一下这个 merge 函数。

sort 函数对 nums[lo..mid] 和 nums[mid+1..hi] 递归排序完成之后，我们没有办法原地把它俩合并，所以需要 copy 到 temp 数组里面，然后通过类似于前文 单链表的六大技巧 中合并有序链表的双指针技巧将 nums[lo..hi] 合并成一个有序数组：

注意我们不是在 merge 函数执行的时候 new 辅助数组，而是提前把 temp 辅助数组 new 出来了，这样就避免了在递归中频繁分配和释放内存可能产生的性能问题。

再说一下归并排序的时间复杂度，虽然大伙儿应该都知道是 O(NlogN)，但不见得所有人都知道这个复杂度怎么算出来的。

前文 动态规划详解 说过递归算法的复杂度计算，就是子问题个数 x 解决一个子问题的复杂度。对于归并排序来说，时间复杂度显然集中在 merge 函数遍历 nums[lo..hi] 的过程，但每次 merge 输入的 lo 和 hi 都不同，所以不容易直观地看出时间复杂度。

执行的次数是二叉树节点的个数，每次执行的复杂度就是每个节点代表的子数组的长度，所以总的时间复杂度就是整棵树中「数组元素」的个数。

所以从整体上看，这个二叉树的高度是 logN，其中每一层的元素个数就是原数组的长度 N，所以总的时间复杂度就是 O(NlogN)。

其他应用

除了最基本的排序问题，归并排序还可以用来解决力扣第 315 题「 计算右侧小于当前元素的个数」：

拍脑袋的暴力解法就不说了，嵌套 for 循环，平方级别的复杂度。

这题和归并排序什么关系呢，主要在 merge 函数，我们在使用 merge 函数合并两个有序数组的时候，其实是可以知道一个元素 nums[i] 后边有多少个元素比 nums[i] 小的。

具体来说，比如这个场景：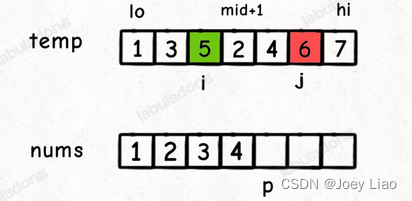

这时候我们应该把 temp[i] 放到 nums[p] 上，因为 temp[i] < temp[j]。

但就在这个场景下，我们还可以知道一个信息：5 后面比 5 小的元素个数就是 左闭右开区间 [mid + 1, j) 中的元素个数，即 2 和 4 这两个元素：

换句话说，在对 nuns[lo..hi] 合并的过程中，每当执行 nums[p] = temp[i] 时，就可以确定 temp[i] 这个元素后面比它小的元素个数为 j - mid - 1。

当然，nums[lo..hi] 本身也只是一个子数组，这个子数组之后还会被执行 merge，其中元素的位置还是会改变。但这是其他递归节点需要考虑的问题，我们只要在 merge 函数中做一些手脚，叠加每次 merge 时记录的结果即可。

class Solution {
    private class Pair {
        int val, id;
        Pair(int val, int id) {
            // 记录数组的元素值
            this.val = val;
            // 记录元素在数组中的原始索引
            this.id = id;
        }
    }
    
    // 归并排序所用的辅助数组
    private Pair[] temp;
    // 记录每个元素后面比自己小的元素个数
    private int[] count;
    
    // 主函数
    public List<Integer> countSmaller(int[] nums) {
        int n = nums.length;
        count = new int[n];
        temp = new Pair[n];
        Pair[] arr = new Pair[n];
        // 记录元素原始的索引位置，以便在 count 数组中更新结果
        for (int i = 0; i < n; i++)
            arr[i] = new Pair(nums[i], i);
        
        // 执行归并排序，本题结果被记录在 count 数组中
        sort(arr, 0, n - 1);
        
        List<Integer> res = new LinkedList<>();
        for (int c : count) res.add(c);
        return res;
    }
    
    // 归并排序
    private void sort(Pair[] arr, int lo, int hi) {
        if (lo == hi) return;
        int mid = lo + (hi - lo) / 2;
        sort(arr, lo, mid);
        sort(arr, mid + 1, hi);
        merge(arr, lo, mid, hi);
    }
    
    // 合并两个有序数组
    private void merge(Pair[] arr, int lo, int mid, int hi) {
        for (int i = lo; i <= hi; i++) {
            temp[i] = arr[i];
        }
        
        int i = lo, j = mid + 1;
        for (int p = lo; p <= hi; p++) {
            if (i == mid + 1) {
                arr[p] = temp[j++];
            } else if (j == hi + 1) {
                arr[p] = temp[i++];
                // 更新 count 数组
                count[arr[p].id] += j - mid - 1;
            } else if (temp[i].val > temp[j].val) {
                arr[p] = temp[j++];
            } else {
                arr[p] = temp[i++];
                // 更新 count 数组
                count[arr[p].id] += j - mid - 1;
            }
        }
    }
}

因为在排序过程中，每个元素的索引位置会不断改变，所以我们用一个 Pair 类封装每个元素及其在原始数组 nums 中的索引，以便 count 数组记录每个元素之后小于它的元素个数。

翻转对

看一下力扣第 493 题「 翻转对」

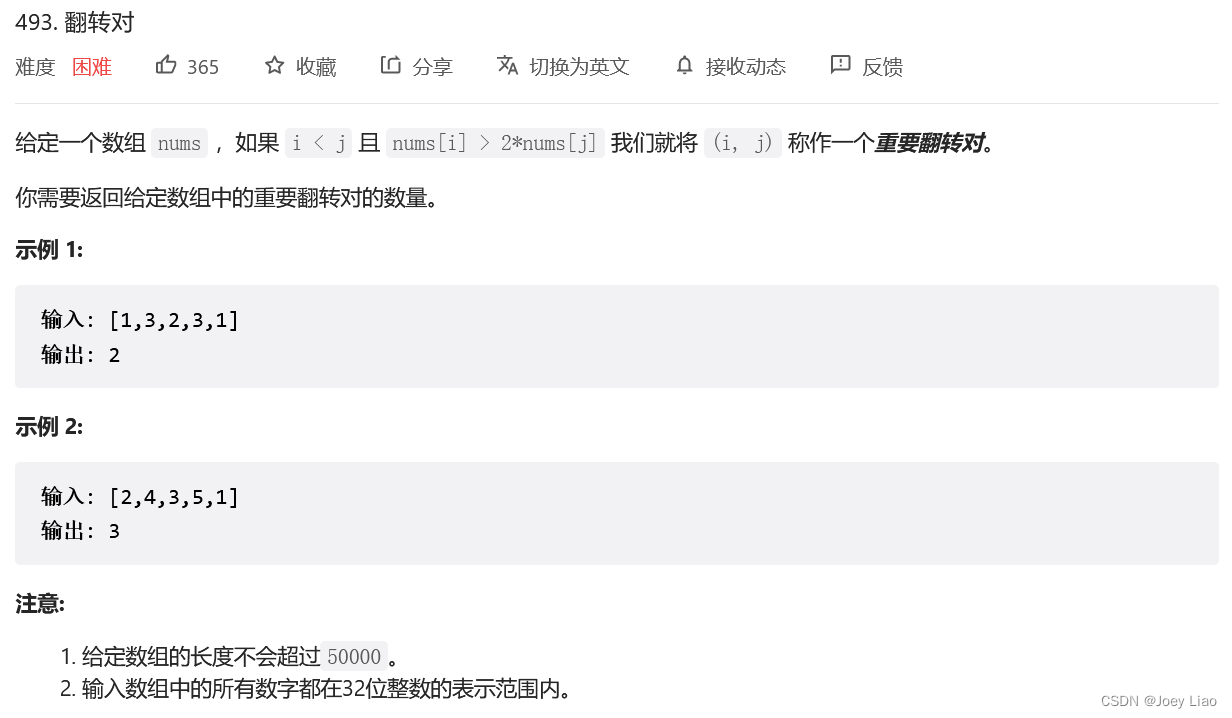
所以解题的思路当然还是要在 merge 函数中做点手脚，当 nums[lo..mid] 和 nums[mid+1..hi] 两个子数组完成排序后，对于 nums[lo..mid] 中的每个元素 nums[i]，去 nums[mid+1..hi] 中寻找符合条件的 nums[j] 就行了。

代码如下：

class Solution {
    int res=0;
    int[] temp;//,doubleTemp;
    public int reversePairs(int[] nums) {
        int n=nums.length;
        temp=new int[n];
        mergeSort(nums,0,n-1);
        return res;
    }

    public void mergeSort(int[] nums,int left,int right){
        if(left==right){
            return;
        }
        int mid=left+(right-left)/2;
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);
        merge(nums,left,mid,right);
    }
    public void merge(int[] nums,int left,int mid,int right){
        for(int i=left;i<=right;i++){
            temp[i]=nums[i];
        }
        *************************************************和普通的归并排序的差别在此
        int end=mid+1;
        for(int i=left;i<=mid;i++){
            while(end<=right&&(long)nums[i]>(long)nums[end]*2){
                end++;
            }
            res+=end-(mid+1);
        }
        ************************************************
        int i=left,j=mid+1;
        for(int k=left;k<=right;k++){
            if(i==mid+1){
                nums[k]=temp[j++];
            }else if(j==right+1){
                nums[k]=temp[i++];
            }else if(temp[i]<temp[j]){
                nums[k]=temp[i++];
            }else{
                nums[k]=temp[j++];
            }
        }
    }
}

区间和的个数

最后来看一道难度更大的题目，力扣第 327 题「 区间和的个数」：

简单说，题目让你计算元素和落在 [lower, upper] 中的所有子数组的个数。

拍脑袋的暴力解法我就不说了，依然是嵌套 for 循环，这里还是说利用归并排序实现的高效算法。

首先，解决这道题需要快速计算子数组的和，需要创建一个前缀和数组 preSum 来辅助我们迅速计算区间和。

我继续用比较数学的语言来表述下这道题，题目让你通过 preSum 数组求一个 count 数组，使得：

count[i] = COUNT(j) where lower <= preSum[j] - preSum[i] <= upper

然后请你求出这个 count 数组中所有元素的和。

private int lower, upper;

public int countRangeSum(int[] nums, int lower, int upper) {
    this.lower = lower;
    this.upper = upper;
    // 构建前缀和数组，注意 int 可能溢出，用 long 存储
    long[] preSum = new long[nums.length + 1];
    for (int i = 0; i < nums.length; i++) {
        preSum[i + 1] = (long)nums[i] + preSum[i];
    }
    // 对前缀和数组进行归并排序
    sort(preSum);
    return count;
}

private long[] temp;

public void sort(long[] nums) {
    temp = new long[nums.length];
    sort(nums, 0, nums.length - 1);
}

private void sort(long[] nums, int lo, int hi) {
    if (lo == hi) {
        return;
    }
    int mid = lo + (hi - lo) / 2;
    sort(nums, lo, mid);
    sort(nums, mid + 1, hi);
    merge(nums, lo, mid, hi);
}

private int count = 0;

private void merge(long[] nums, int lo, int mid, int hi) {
    for (int i = lo; i <= hi; i++) {
        temp[i] = nums[i];
    }
    
    // 在合并有序数组之前加点私货（这段代码会超时）
    // for (int i = lo; i <= mid; i++) {
    //     for (int j = mid + 1; j <= hi; k++) {
    //         // 寻找符合条件的 nums[j]
    //         long delta = nums[j] - nums[i];
    //         if (delta <= upper && delta >= lower) {
    //             count++;
    //         }
    //     }
    // }
    
    // 进行效率优化
    // 维护左闭右开区间 [start, end) 中的元素和 nums[i] 的差在 [lower, upper] 中
    int start = mid + 1, end = mid + 1;
    for (int i = lo; i <= mid; i++) {
        // 如果 nums[i] 对应的区间是 [start, end)，
        // 那么 nums[i+1] 对应的区间一定会整体右移，类似滑动窗口
        while (start <= hi && nums[start] - nums[i] < lower) {
            start++;
        }
        while (end <= hi && nums[end] - nums[i] <= upper) {
            end++;
        }
        count += end - start;
    }

    // 数组双指针技巧，合并两个有序数组
    int i = lo, j = mid + 1;
    for (int p = lo; p <= hi; p++) {
        if (i == mid + 1) {
            nums[p] = temp[j++];
        } else if (j == hi + 1) {
            nums[p] = temp[i++];
        } else if (temp[i] > temp[j]) {
            nums[p] = temp[j++];
        } else {
            nums[p] = temp[i++];
        }
    }
}

我们依然在 merge 函数合并有序数组之前加了一些逻辑，如果看过前文 滑动窗口核心框架，这个效率优化有点类似维护一个滑动窗口，让窗口中的元素和 nums[i] 的差落在 [lower, upper] 中。

比如本文讲的归并排序算法，递归的 sort 函数就是二叉树的遍历函数，而 merge 函数就是在每个节点上做的事情，有没有品出点味道？