当前位置:网站首页>Knight defeats demon king (Backpack & DP)
Knight defeats demon king (Backpack & DP)
2022-07-07 06:18:00 【Harris-H】
The knight defeated the demon king ( knapsack &dp)
Because the plan is different , It depends on the energy and difference used by a knight .
Therefore, we consider using backpacks to deal with the energy used by each Knight i i i The biggest damage , When seeking the maximum, in order to include all cases .
Then proceed dp, Make f ( i , j ) f(i,j) f(i,j) Before presentation i i i Knights caused j j j Number of schemes for point damage .
Specially , f ( i , m ) f(i,m) f(i,m) Before presentation i i i Knights cause greater than or equal to j j j Number of schemes for point damage .
Then proceed dp that will do .
Time complexity : O ( n × 3000 ) O(n\times 3000) O(n×3000)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int mod = 998244353;
int n, m;
int fans[3009][3009], ff[3009];
int a[3009], b[3009];
void solved() {
cin >> n >> m;
fans[0][0] = 1;
int s;
for(int ttf = 1; ttf <= n; ttf ++) {
cin >> s;
for(int i = 0; i < s; i ++) cin >> a[i];
for(int i = 0; i < s; i ++) cin >> b[i];
for(int i = 0; i <= 3000; i ++) ff[i] = 0; /// initialization dp Array
for(int i = 0; i < s; i ++) {
/// Find out the maximum attack power that each energy consumption of the current knight can cause
for(int j = 3000; j >= b[i]; j --) {
if(ff[j - b[i]] || j - b[i] == 0)
ff[j] = max(ff[j - b[i]] + a[i], ff[j]);
}
} /// n Total time complexity of knights : sum(s) * 3000
for(int i = 0; i <= 3000; i ++) {
if(ff[i] == 0 && i != 0) continue; /// Some values cannot be represented , The magnitude of the value that can be represented is sum(b)
if(ff[i] > m) ff[i] = m; /// Attack overflow processing
for(int j = 0; j < ff[i]; j ++) /// Here is the number of schemes in the attack overflow part , It needs to be calculated separately
fans[ttf][m] = (fans[ttf][m] + fans[ttf - 1][m - j]) % mod;
for(int j = m; j >= ff[i]; j --) /// This for And the one above for The total time complexity of is : sum(b) * m
fans[ttf][j] = (fans[ttf][j] + fans[ttf - 1][j - ff[i]]) % mod;
} /// n The total time complexity of a knight here : n * 3000
} /// Total time complexity : sum(s) * 3000 + n * 3000 + sum(b) * m
cout << fans[n][m];
}
int main() {
// int ttx; cin >> ttx; while(ttx --)
solved();
return 0;
}
边栏推荐
- 【FPGA教程案例14】基于vivado核的FIR滤波器设计与实现
- Detailed explanation of platform device driver architecture in driver development
- jmeter 函数助手 — — 随机值、随机字符串、 固定值随机提取
- Check point: the core element for enterprises to deploy zero trust network (ztna)
- On the discrimination of "fake death" state of STC single chip microcomputer
- 「解析」FocalLoss 解决数据不平衡问题
- [SOC FPGA] custom IP PWM breathing lamp
- Red hat install kernel header file
- cf:C. Column Swapping【排序 + 模擬】
- @Detailed differences between pathvariable and @requestparam
猜你喜欢
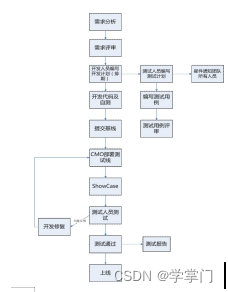
软件测试的几个关键步骤,你需要知道
![[InstallShield] Introduction](/img/df/4522d06510ff918d00659b8358368f.jpg)
[InstallShield] Introduction
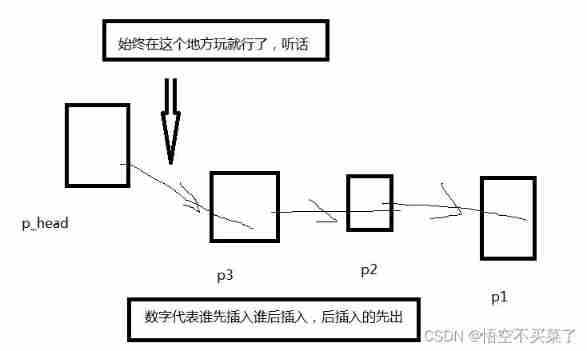
Chain storage of stack

Markdown displays pictures side by side

DC-7靶机
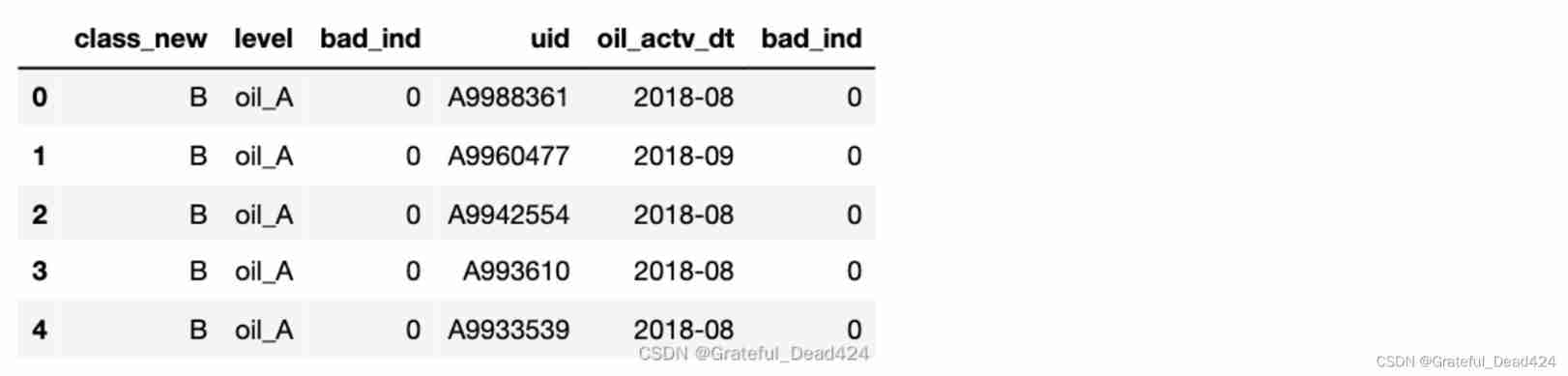
Financial risk control practice - decision tree rule mining template
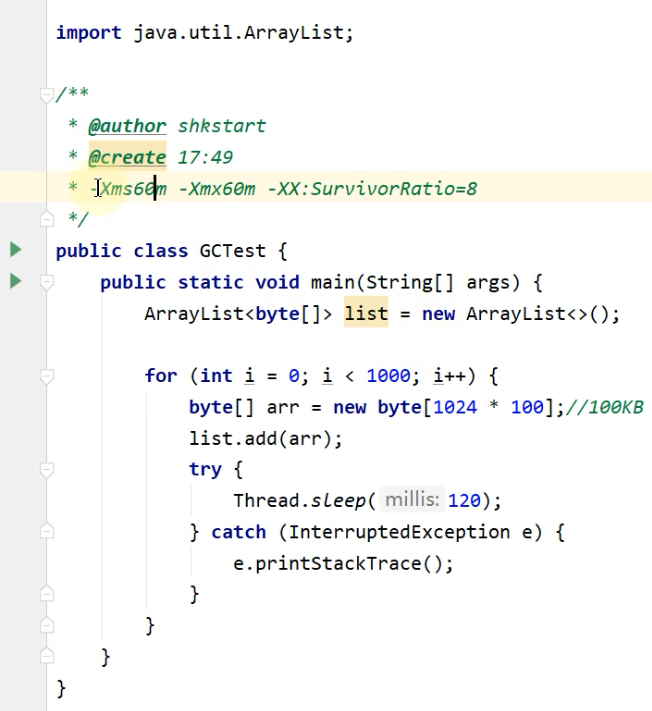
JVM命令之- jmap:导出内存映像文件&内存使用情况
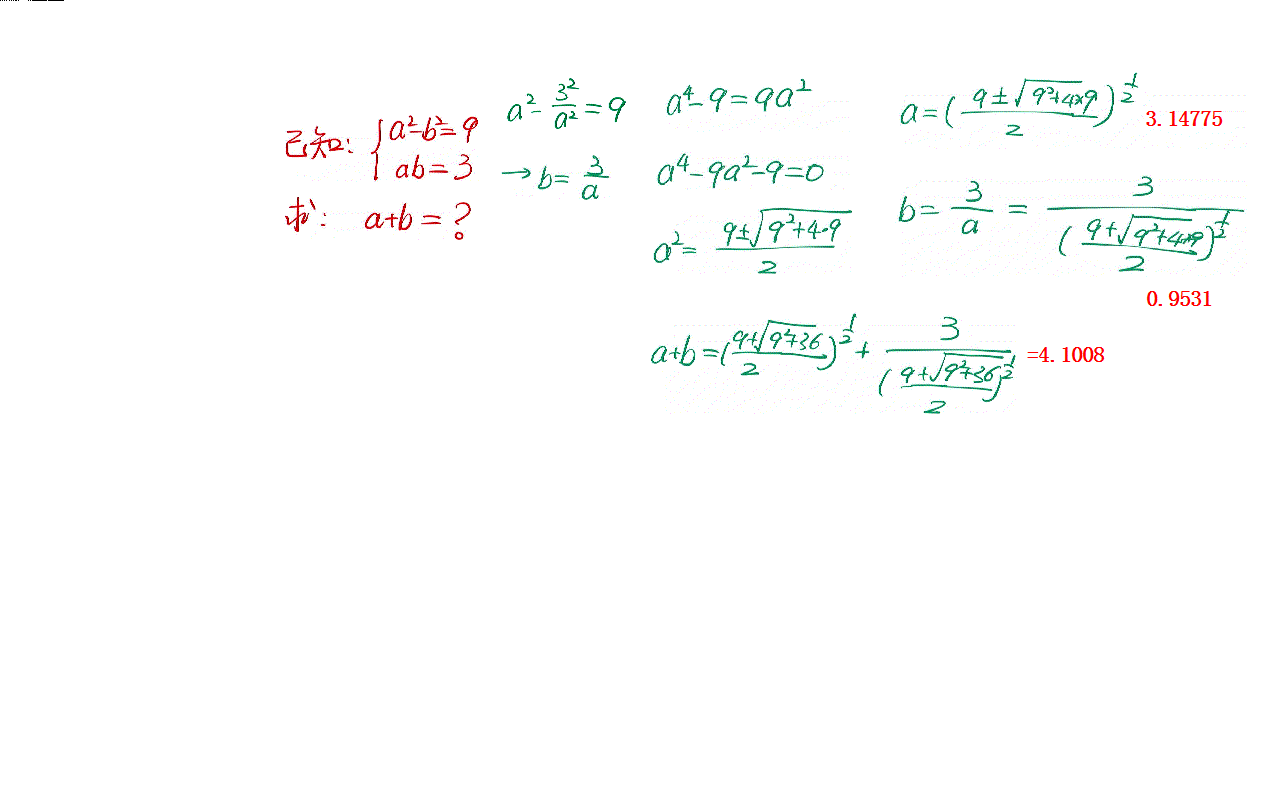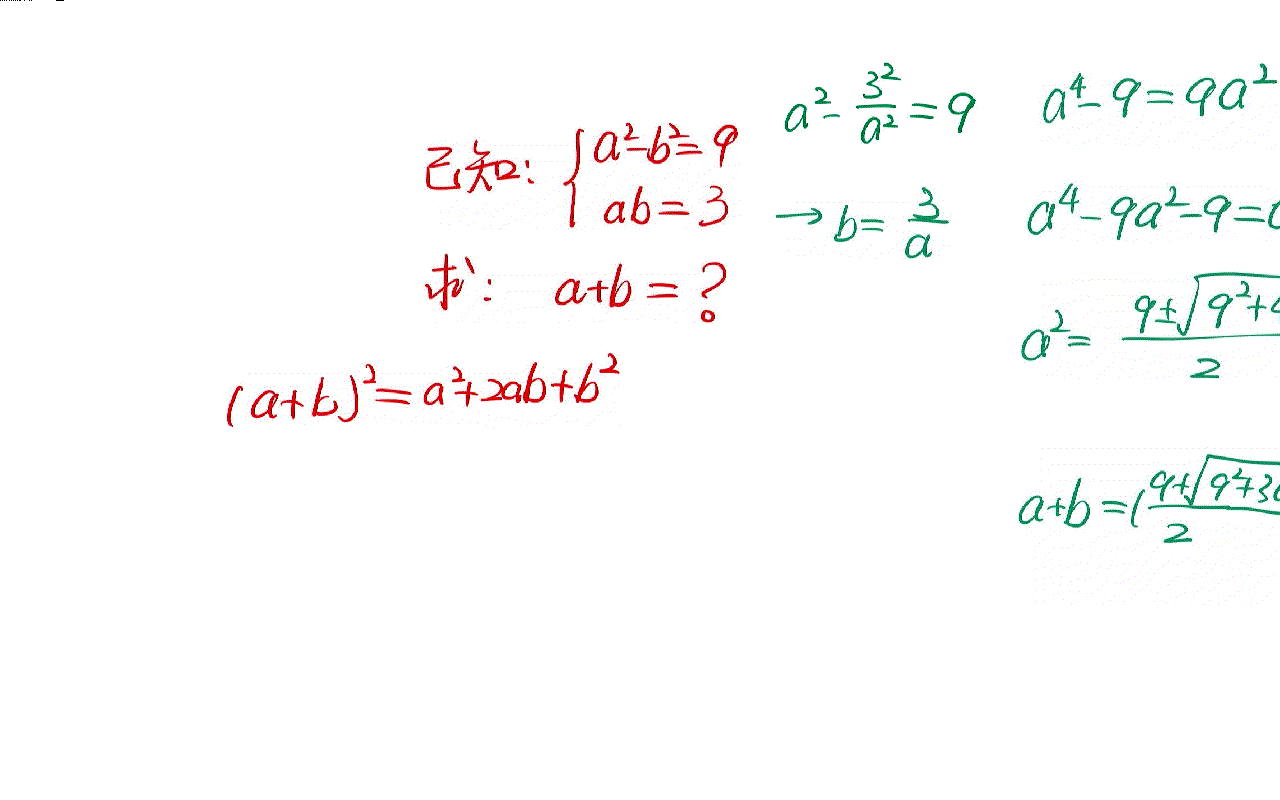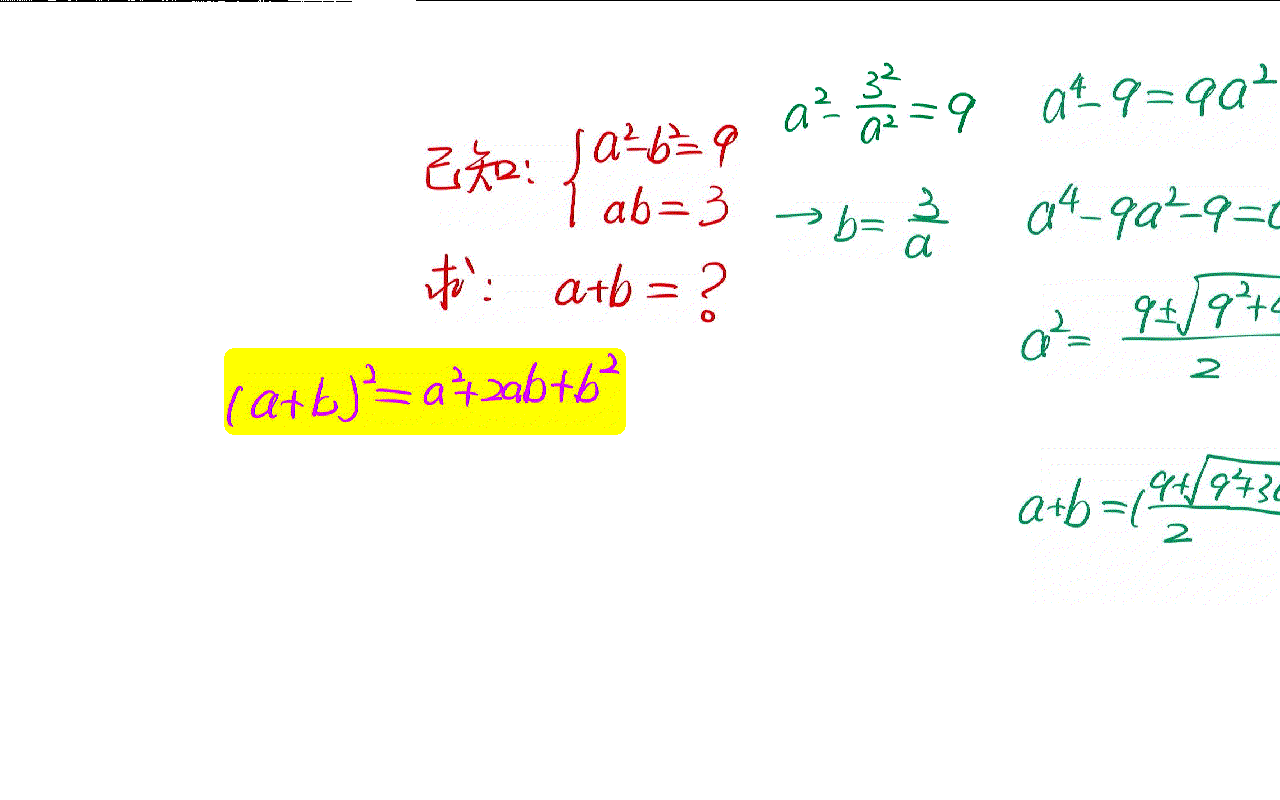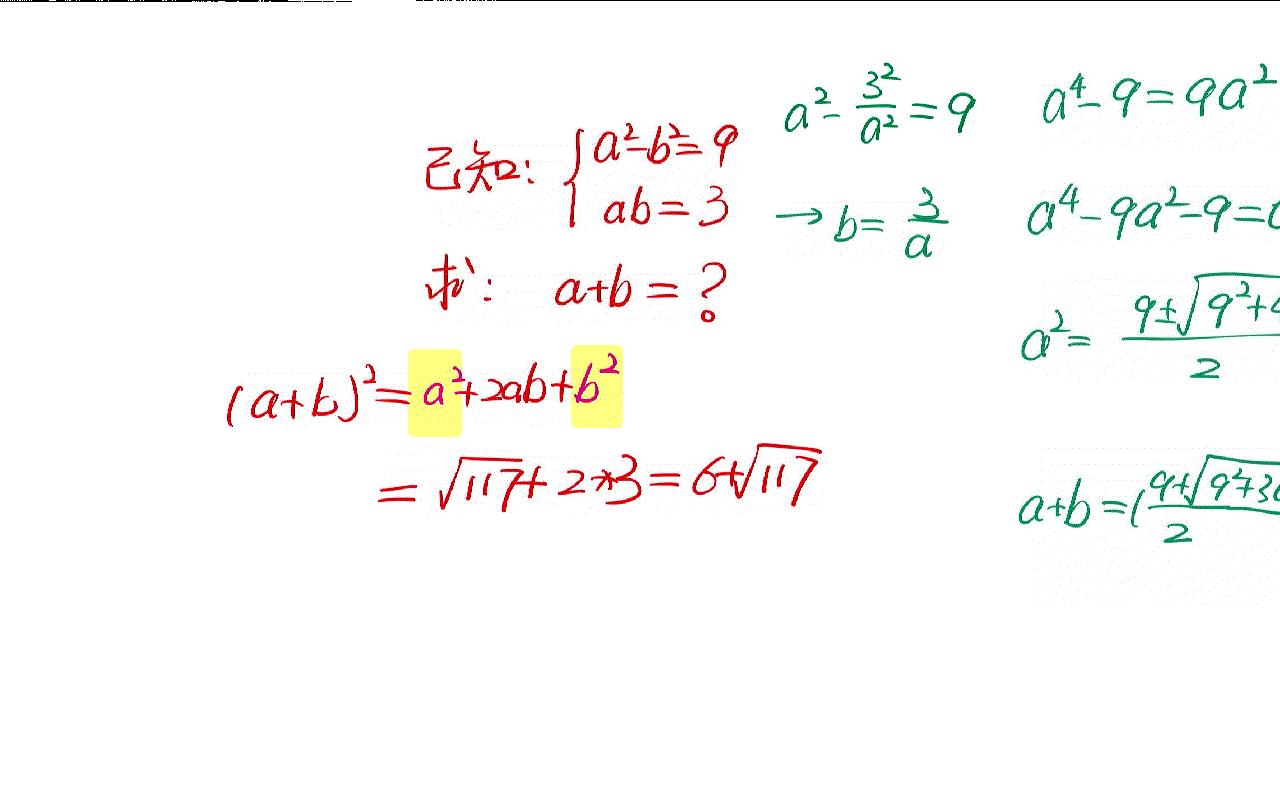
The solution of a simple algebraic problem

Jstack of JVM command: print thread snapshots in JVM
If you don't know these four caching modes, dare you say you understand caching?
随机推荐
Experience sharing of contribution of "management world"
go-microservice-simple(2) go-Probuffer
苹果cms V10模板/MXone Pro自适应影视电影网站模板
Niuke Xiaobai monthly race 52 E. sum logarithms in groups (two points & inclusion and exclusion)
POI excel export, one of my template methods
Calculation model FPS
改变ui组件原有样式
693. 行程排序
Database notes 04
JVM监控及诊断工具-命令行篇
外设驱动库开发笔记43:GPIO模拟SPI驱动
「解析」FocalLoss 解决数据不平衡问题
980. Different path III DFS
Oracle迁移中关于大容量表使用数据泵(expdp、impdp)导出导入容易出现的问题和注意事项
Bbox regression loss function in target detection -l2, smooth L1, IOU, giou, Diou, ciou, focal eiou, alpha IOU, Siou
C. colonne Swapping [tri + Simulation]
Experience of Niuke SQL
Storage of dental stem cells (to be continued)
基于ADAU1452的DSP及DAC音频失真分析
SubGHz, LoRaWAN, NB-IoT, 物联网