当前位置:网站首页>Slipper —— 虚点,最短路
Slipper —— 虚点,最短路
2022-08-04 00:56:00 【小酒窝.】
题意
给定根节点为 1,节点数为 n n n 的一棵树,n-1 条边有边权 w i w_i wi。
如果两个点 u , v u, v u,v 深度之差为 k ( ∣ d e p u − d e p v ∣ = k ) k\ (|dep_u−dep_v|=k) k (∣depu−depv∣=k) ,可以直接相互到达,花费为 p p p。
给定起点和终点,问从起点到终点的最小花费。
2 ≤ n ≤ 1 0 6 , 1 ≤ u , v ≤ n , 1 ≤ w ≤ 1 0 6 . 2≤n≤10^6,\ 1≤u,v≤n,\ 1≤w≤10^6. 2≤n≤106, 1≤u,v≤n, 1≤w≤106.
1 ≤ k ≤ m a x u ⊆ V ( d e p u ) , 0 ≤ p ≤ 1 0 6 . 1≤k≤max_u⊆V(dep_u),\ 0≤p≤10^6. 1≤k≤maxu⊆V(depu), 0≤p≤106.
思路
两层节点之间花费 p 直接到达,那么就可以连边。
但是如果直接连边的话,假设两层点数分别为 n, m,那么连边数为 n*m,边数很多。
是否可以少连边呢?
在两层之间建一个虚点,上层所有节点向虚点连一条由向边,边权为 p;从虚点向下层所有节点连一条有向边,边权为 0。连边数 n+m。
注意是有向边!
那么这样上层任一节点到下层任一节点的花费仍是 p,但是少建很多边!
这题就是这个思路,能够直接到达的两层之间都建立一个虚点,两层节点向这个虚点连边,然后就可以直接跑最短路了。
需要注意,输入数量到达 5e6,要换scanf,最好用快读。
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
#define PII pair<int,int>
#define pb push_back
#define fi first
#define se second
#define endl '\n'
static char buf[100000],*pa=buf,*pd=buf;
#define gc pa==pd&&(pd=(pa=buf)+fread(buf,1,100000,stdin),pa==pd)?EOF:*pa++
inline int read()
{
register int x(0);register char c(gc);
while(c<'0'||c>'9')c=gc;
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=gc;
return x;
}
const int N = 1000010, mod = 1e9+7;
int T, n, m;
int a[N];
vector<PII> e[N*2];
int k, p, st, en;
int dep[N];
vector<int> v[N];
int maxdep;
int dist[N*2], f[N*2];
void bfs()
{
for(int i=1;i<=n;i++) dep[i] = 0;
dep[1] = 1;
queue<int> que;
que.push(1);
v[1].push_back(1);
while(que.size())
{
int x = que.front(); que.pop();
for(PII it : e[x])
{
int tx = it.fi;
if(dep[tx]) continue;
dep[tx] = dep[x] + 1;
v[dep[tx]].push_back(tx);
maxdep = max(maxdep, dep[tx]); //可以维护最大深度,以减少后面的初始化和建边
que.push(tx);
}
}
}
int dij()
{
for(int i=1;i<=2*n;i++) dist[i] = 1e18, f[i] = 0;
dist[st] = 0;
priority_queue<PII, vector<PII>, greater<PII> > que;
que.push({
0, st});
while(que.size())
{
int x = que.top().se; que.pop();
if(f[x]) continue;
f[x] = 1;
if(x == en) return dist[x];
for(auto it : e[x])
{
int tx = it.fi, dis = it.se;
if(dist[tx] > dist[x] + dis)
dist[tx] = dist[x] + dis, que.push({
dist[tx], tx});
}
}
return -1;
}
void init()
{
for(int i=1;i<=n;i++) v[i].clear();
for(int i=1;i<=2*n;i++) e[i].clear();
maxdep = 1;
}
signed main(){
T = read();
while(T--)
{
n = read();
init();
for(int i=1;i<n;i++)
{
int x, y, z;
x = read(), y = read(), z = read();
e[x].push_back({
y, z});
e[y].push_back({
x, z});
}
k = read(), p = read();
st = read(), en = read();
bfs();
for(int i=1;i<=n;i++)
{
int tx = i + k;
if(tx > maxdep) break; //大于最大深度就不用管了
for(int t : v[i]) e[t].push_back({
n+i, p});
for(int t : v[tx]) e[n+i].push_back({
t, 0});
}
printf("%lld\n", dij());
}
return 0;
}
经验
建立虚点,很妙的做法。
还看到一个应用:
如果有若干个起点,若干个终点,求任一起点到任一终点的最短距离。
这时如果朴素做的话就要跑 n 次最短路,但是可以建一个虚拟源点,向所有起点连边,权值为 0,那么从这个源点跑最短路只需要一次即可。
很妙!
边栏推荐
- typescript53 - generic constraints
- 电子制造企业部署WMS仓储管理系统的好处是什么
- typescript58 - generic classes
- Nanoprobes丨Nanogold-抗体和链霉亲和素偶联物
- 第1章:初识数据库与MySQL----MySQL安装
- LeetCode third topic (the Longest Substring Without Repeating Characters) trilogy # 3: two optimization
- 【性能优化】MySQL常用慢查询分析工具
- NLP resources that must be used for projects [Classified Edition]
- Eight things to pay attention to in spot silver
- js函数防抖和函数节流及其使用场景
猜你喜欢

Nanoprobes Mono- Sulfo -NHS-Nanogold的使用和应用
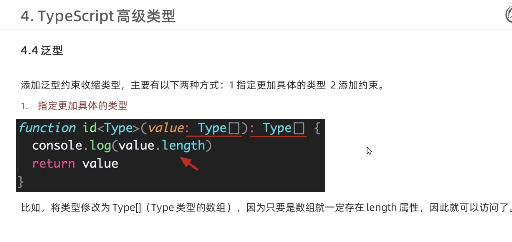
typescript53 - generic constraints

SQL优化的一些建议,希望可以帮到和我一样被SQL折磨的你
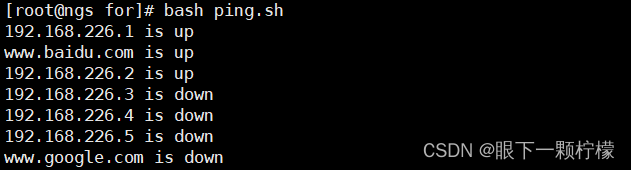
Shell编程之循环语句(for、while)

2022年8月份DAMA-CDGA/CDGP数据治理认证招生简章
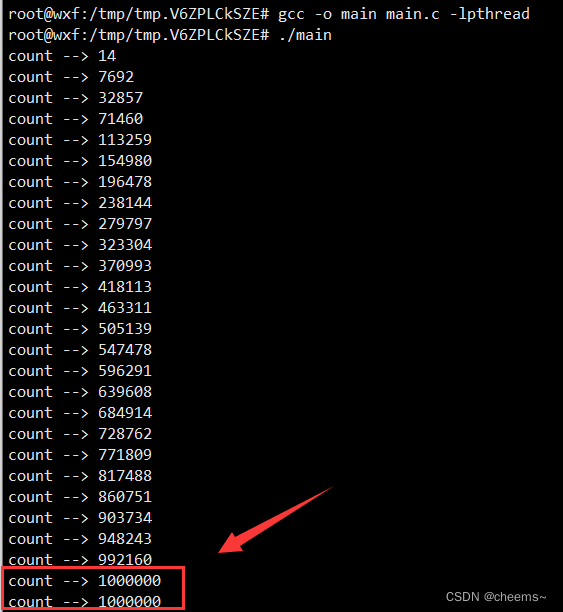
互斥锁、读写锁、自旋锁,以及原子操作指令xaddl、cmpxchg的使用场景剖析

Web3 security risks daunting?How should we respond?
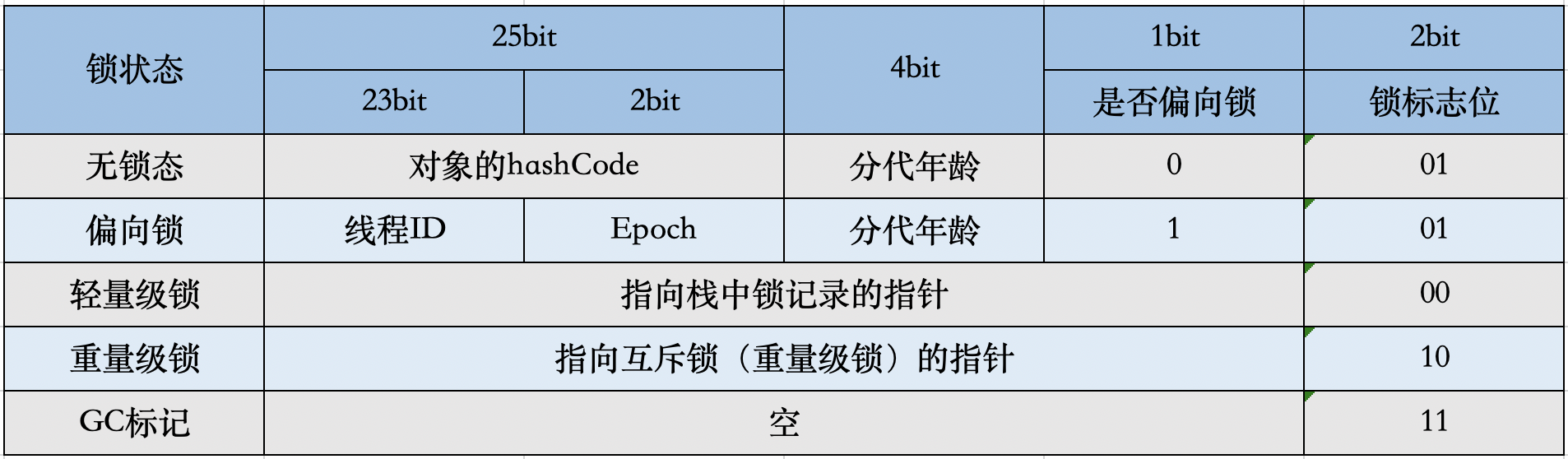
面试必问的HashCode技术内幕

After building the pytorch environment, the pip and conda commands cannot be used

共享新能源充电桩充电站建设需要些什么流程及资料?
随机推荐
求解同余方程 数论 扩展欧几里得
高斯推断推导
C# wpf使用ffmpeg命令行实现录屏
分析:Nomad Bridge黑客攻击的独特之处
typescript52 - simplify generic function calls
全面讲解 Handler机制原理解析 (小白必看)
WMS仓储管理系统能解决电子行业哪些仓库管理问题
优秀的测试/开发程序员,是怎样修炼的?步步为营地去执行......
"Miscellaneous" barcode by Excel as a string
Node.js的基本使用(三)数据库与身份认证
LeetCode third topic (the Longest Substring Without Repeating Characters) trilogy # 3: two optimization
typescript50 - type specification between cross types and interfaces
typescript57-数组泛型接口
Read FastDFS in one article
Eight things to pay attention to in spot silver
GraphQL背后处理及执行过程是什么
【虚拟化生态平台】虚拟化平台搭建
第1章:初识数据库与MySQL----MySQL安装
Talking about the future development direction of my country's industrial parks
typescript48 - type compatibility between functions