当前位置:网站首页>求解同余方程 数论 扩展欧几里得
求解同余方程 数论 扩展欧几里得
2022-08-03 23:58:00 【Rachel caramel】
题面: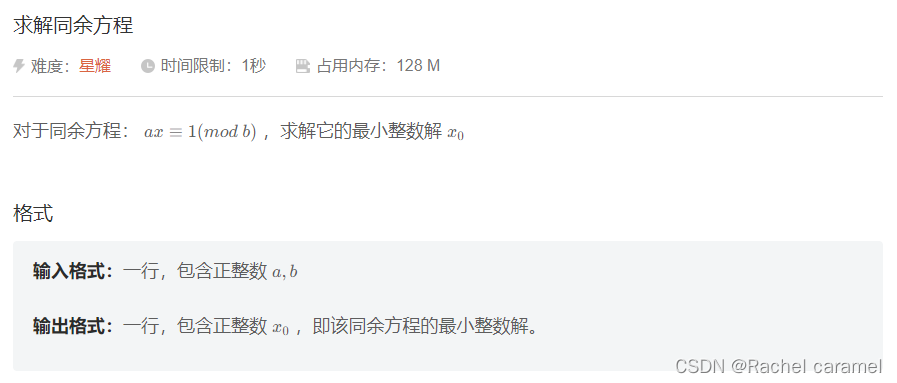

思路:
a ⋅ x = b ⋅ y + 1 a ⋅ x − b ⋅ y = 1 因为y的取值是任意的,因此可以将这个式子看成: a ⋅ x + b ⋅ y = 1 因为题目保证有解,所以a和b是互质的,即 gcd ( a , b ) = 1 而扩展欧几里得就是用来求形如: a ⋅ x + b ⋅ = c 的不定方程的整数解的 这里需要再补充一个裴蜀定理: 若 a , b 为整数,那么一定存在 a ⋅ x + b ⋅ y = gcd ( a , b ) 即 a ⋅ x + b ⋅ y 的值一定是 gcd ( a , b ) 的倍数 先考虑边界情况 a ⋅ 1 + b ⋅ 0 = gcd ( a , b ) , 此时, x = 1 , y = 0 然后考虑一般情况,假设某一次得到的解是 x 0 、 y 0 b ⋅ x 0 + ( a m o d b ) ⋅ y 0 = gcd ( a , b ) b ⋅ x 0 + ( a − ⌊ a b ⌋ ⋅ b ) ⋅ y 0 = gcd ( a , b ) a ⋅ y 0 + b ⋅ ( x 0 − ⌊ a b ⌋ ⋅ y 0 ) = gcd ( a , b ) 由此可得: x = y 0 , y = x 0 − ⌊ a b ⌋ ⋅ y 0 已知任意一组解 x 0 , y 0 通解为: x = x 0 + b gcd ( a , b ) ⋅ n x = x 0 + b gcd ( a , b ) ⋅ n a\cdot x=b\cdot y +1\\ a\cdot x-b\cdot y =1\\ \text{因为y的取值是任意的,因此可以将这个式子看成:}\\ a\cdot x+b\cdot y =1\\ \text{因为题目保证有解,所以a和b是互质的,即}\gcd(a,b)=1\\ \text{而扩展欧几里得就是用来求形如:} a\cdot x+b\cdot=c\text {的不定方程的整数解的}\\ \text{这里需要再补充一个裴蜀定理:}\\ \text{若}a,b\text{为整数,那么一定存在}a\cdot x+b\cdot y=\gcd(a,b)\\ \text{即}a\cdot x+b\cdot y \text{的值一定是}\gcd(a,b)\text{的倍数}\\ \text{先考虑边界情况}a\cdot 1+b\cdot 0=\gcd(a,b),\text{此时,}x=1,y=0\\ \text{然后考虑一般情况,假设某一次得到的解是}x_0、y_0\\ b\cdot x_0+(a\bmod b)\cdot y_0=\gcd(a,b)\\ b\cdot x_0+(a-\lfloor \frac a b \rfloor\cdot b)\cdot y_0=\gcd(a,b)\\ a\cdot y_0+b\cdot (x_0-\lfloor \frac a b \rfloor\cdot y_0)=\gcd(a,b)\\ \text{由此可得:} x=y_0 ,y=x_0-\lfloor \frac a b \rfloor\cdot y_0\\ \text{已知任意一组解}x_0,y_0\text{通解为:} \\ x=x0+ \frac{b} {\gcd (a,b)}\cdot n\\ x=x0+ \frac{b} {\gcd (a,b)}\cdot n\\ a⋅x=b⋅y+1a⋅x−b⋅y=1因为y的取值是任意的,因此可以将这个式子看成:a⋅x+b⋅y=1因为题目保证有解,所以a和b是互质的,即gcd(a,b)=1而扩展欧几里得就是用来求形如:a⋅x+b⋅=c的不定方程的整数解的这里需要再补充一个裴蜀定理:若a,b为整数,那么一定存在a⋅x+b⋅y=gcd(a,b)即a⋅x+b⋅y的值一定是gcd(a,b)的倍数先考虑边界情况a⋅1+b⋅0=gcd(a,b),此时,x=1,y=0然后考虑一般情况,假设某一次得到的解是x0、y0b⋅x0+(amodb)⋅y0=gcd(a,b)b⋅x0+(a−⌊ba⌋⋅b)⋅y0=gcd(a,b)a⋅y0+b⋅(x0−⌊ba⌋⋅y0)=gcd(a,b)由此可得:x=y0,y=x0−⌊ba⌋⋅y0已知任意一组解x0,y0通解为:x=x0+gcd(a,b)b⋅nx=x0+gcd(a,b)b⋅n
代码:
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
const int maxn=111111;
int a,b,x,y;
void exgcd(int a,int b,int *x,int *y)//扩展欧几里得算法
{
//cout<<"a="<<a<<" "<<"b="<<b<<" "<<"x="<<*x<<" "<<"y="<<*y<<endl;
if(b==0)
{
*x=1,*y=0;
return;
}
exgcd(b,a%b,x,y); //r=GCD(a,b)=GCD(b, a%b)
//cout<<"!!!a="<<a<<" "<<"b="<<b<<" "<<"x="<<*x<<" "<<"y="<<*y<<endl;
int t=*x;
*x=*y;
*y=t-a/b*(*y) ;
}
int main()
{
cin>>a>>b;
exgcd(a,b,&x,&y);
//cout<<"x="<<x<<" "<<"b="<<b<<endl;
while(x<0) x+=b;
cout<<x<<endl;
return 0;
}
边栏推荐
- MCS-51单片机,定时1分钟,汇编程序
- 全球首款量产,获定点最多!这家AVP Tier1如何实现领跑?
- 栈的压入、弹出序列
- JS获得URL超链接的参数值
- Fluorescein-PEG-CLS, cholesterol-polyethylene glycol-fluorescein scientific research reagent
- The world's first mass production, with the most fixed points!How does this AVP Tier1 lead?
- 汉字风格迁移---结合本地和全局特征学习的中文字体迁移
- 双目IMU标定kalibr
- 用栈实现队列
- 小身材有大作用——光模块基础知识(一)
猜你喜欢
随机推荐
MPLS综合实验
Unity2021 releases WebGL fog effect disappearing problem
Justin Sun was invited to attend the 36氪 Yuan Universe Summit and delivered a keynote speech
V8中的快慢数组(附源码、图文更易理解)
RSS订阅微信公众号初探-feed43
七夕活动浪漫上线,别让网络拖慢和小姐姐的开黑时间
【并发编程】ReentrantLock的lockInterruptibly()方法源码分析
XSLT – 编辑 XML概述
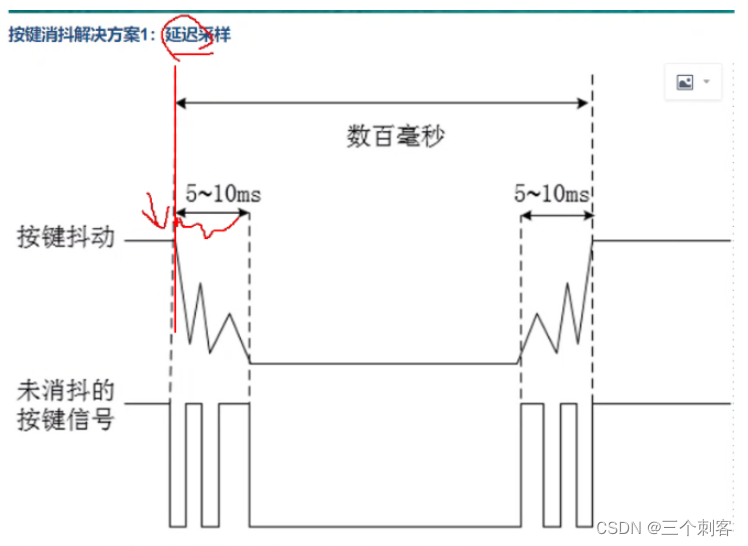
FPGA按键消抖+蜂鸣器
ping数据包中的进程号
XSLT – 服务器端概述
详谈RDMA技术原理和三种实现方式
带你造轮子,自定义一个随意拖拽可吸边的悬浮View组件
Jar a key generation document database
使用unbound在RHEL7上搭建DNS服务
我的祖国
The longest substring that cannot have repeating characters in a leetcode/substring
Creo 9.0创建几何点
用两个栈模拟队列
重新认识浏览器的渲染过程