当前位置:网站首页>2022 东北四省赛 VP记录/补题
2022 东北四省赛 VP记录/补题
2022-07-03 10:21:00 【HeartFireY】
VP情况
| A | B | C | D | E | F | G | H | I | J | K | L | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 待补 | AC | AC(-6) | AC | AC | 补题 | 补题 | – | AC(-2) | – | AC | AC | – |
A.Encryption
–待补–
B.Capital Progra
题目分析
要求在给定的图上选择一个连通块,使得该连通块到其他点的距离和最小。
考虑贪心的选取,我们可以将图展开,然后从叶节点开始按照逆 B F S BFS BFS序进行删点,删完 n − k n-k n−k个为止。可以用拓扑排序实现这个过程,设 d i s [ i ] dis[i] dis[i]表示该点子树的边数(边权和),在排序过程中更新最大值即可。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e5 + 10;
vector<int> g[N];
int deg[N], dis[N];
inline void solve(){
int n, k; cin >> n >> k;
for(int i = 1; i < n; i++){
int u, v; cin >> u >> v;
g[u].emplace_back(v);
g[v].emplace_back(u);
deg[u]++, deg[v]++;
}
if(n == k){
cout << 0 << endl; return; }
queue<int> q;
for(int i = 1; i <= n; i++) if(deg[i] == 1) dis[i] = 1, q.emplace(i);
int cnt = 0, ans = -1;
while(q.size()){
int u = q.front(); q.pop();
if(++cnt > n - k) break;
ans = max(ans, dis[u]);
for(auto v : g[u]){
dis[v] = max(dis[v], dis[u] + 1);
if(--deg[v] == 1) q.emplace(v);
}
}
cout << ans << endl;
}
signed main(){
solve();
return 0;
}
C.SegmentTree
题目分析
要求在给定的覆盖 [ 1 , m ] [1,m] [1,m]区间的线段树上找 q q q条路径(自行构造),使覆盖的点的数目最大。
首先可以肯定的是,当 q ≥ m q \ge m q≥m时,我们可以选取 m m m个叶子节点进行 A D D ADD ADD操作,从而使得整颗线段树被覆盖。
考虑 q ≤ m q \le m q≤m时,如何选取叶节点使得覆盖点数目最大。
如下图为覆盖区间为 [ 1 , 12 ] [1,12] [1,12]的线段树,我们可以发现贪心选取的规律:
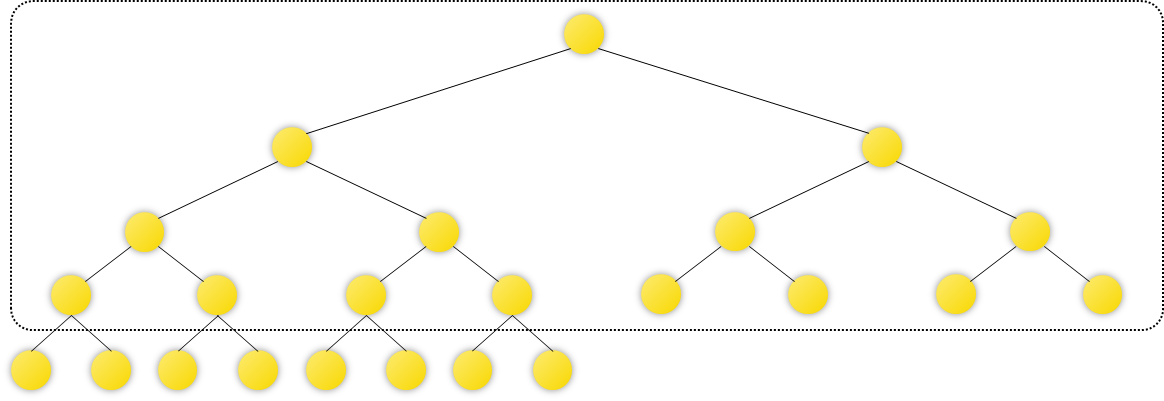
- 对于第一层(共 1 1 1个节点),当操作数 p ≥ 1 p \geq 1 p≥1时可以全部覆盖,否则最多覆盖 q q q个节点(即 0 0 0个节点);
- 对于第二层(共 2 2 2个节点),当操作数 p ≥ 2 p \ge 2 p≥2时可以全部覆盖,否则最多覆盖 q q q个节点;
- 对于第三层(共 4 4 4个节点),当操作数 p ≥ 4 p \ge 4 p≥4时可以全部覆盖,否则最多覆盖 q q q个节点;
- 对于第三层(共 8 8 8个节点),当操作数 p ≥ 8 p \ge 8 p≥8时可以全部覆盖,否则最多覆盖 q q q个节点;
Note: 可以通过求 a r g _ m a x i ( 2 i ≤ m ) arg\_max_i\ (2^i \leq m) arg_maxi (2i≤m)求得最后一个完整层的深度
最后一层由于可能非完整层情况,因此需要进行讨论:当前最后一层共有 12 − 8 = 4 12 - 8 = 4 12−8=4棵子树:
- q ≤ 4 q \leq 4 q≤4,最多选 q q q棵子树被选 1 1 1个节点(保证根节点被贪心选中);
- 4 ≤ q ≤ 8 4 \le q \leq 8 4≤q≤8,所有子树均选择 1 1 1个节点;
- 否则全部选中。
那么按照以上贪心的思路选择即可。
Code
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
void solve(){
int m, q; cin >> m >> q;
int ret = 1, sum = 0;
for(ret = 1; ret < m; ret <<= 1) sum += std::min(ret, q);
int sub = m - (ret >> 1);
if(sub >= q) cout << sum + q << endl;
else if((ret >> 1) >= q) cout << sum + sub << endl;
else cout << sum + sub + min(sub, (q - (ret >> 1))) << endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int _=1;
cin>>_;
while(_--){
solve();
}
}
D.Game
题目分析
给定 n n n堆石子,轮流取石子,不能操作的输。每次选一堆至少取 1 1 1个,剩余的石子可以分配给其它堆。每轮游戏给定询问,要求回答 [ l , r ] [l,r] [l,r]区间的游戏结果。
全 0 0 0的时候,先手必败,那么考虑能够到达该状态的状态:仅有 1 1 1堆石子->先手必胜。
再继续归纳,两堆 1 1 1个石子,此时先手必败,推广该状态,发现任意 A , B A,B A,B满足 A ≠ B A \neq B A=B,均为先手必胜。
推广:发现当 m m m堆石子, m m m为奇数时,先手必败,然后可以猜测仅有偶数堆石子时,先手可能会胜利。
然后继续猜测:设 f ( x ) f(x) f(x)表示数字 x x x在区间 [ l , r ] [l,r] [l,r]的出现次数。 先手必败当且仅当 ∀ x , f ( x ) ≡ 0 ( m o d 2 ) ∀x, f(x) ≡ 0 (mod 2) ∀x,f(x)≡0(mod2)。
具体证明见官方题解…
那么求区间数字出现次数是否全为偶数,直接莫队离线询问即可。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], BLCOK_SIZE = 0;
struct node{
int l, r, id;
const bool operator<(const node &x) const {
int d1 = l / BLCOK_SIZE, d2 = x.l / BLCOK_SIZE;
return d1 < d2 || (d1 == d2 && r < x.r);
}
}ask[N];
int ans[N], cnt[N], nowAns = 0;
inline void op(int x){
cnt[a[x]]++;
cnt[a[x]] & 1 ? nowAns++ : nowAns--;
}
inline void solve(){
int n = 0, q = 0; cin >> n >> q;
for(int i = 1; i <= n; i++) cin >> a[i];
BLCOK_SIZE = int(ceil(pow(n, 0.5)));
for(int i = 1; i <= q; i++){
cin >> ask[i].l >> ask[i].r, ask[i].id = i;
}
sort(ask + 1, ask + 1 + q);
for(int i = 1, l = 1, r = 0; i <= q; i++){
auto q = ask[i];
while(l > q.l) op(--l);
while(r < q.r) op(++r);
while(l < q.l) op(l++);
while(r > q.r) op(r--);
ans[q.id] = nowAns;
}
for(int i = 1; i <= q; i++){
if(ans[i]) cout << "Alice\n";
else cout << "Bob\n";
}
}
signed main(){
solve();
return 0;
}
E.Plus
题目分析
打表找规律,可以发现当 n ≥ 3 n \geq 3 n≥3时,有且仅有 1 1 1组答案满足,为 2 , 3 2, 3 2,3。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
inline void solve(){
int n = 0; cin >> n;
if(n >= 3) cout << "1" << endl << "2 3" << endl;
else cout << "0\n" << endl;
}
signed main(){
solve();
return 0;
}
F.Tree Path
单独见博客:
题目分析
给定一棵树,包含 n n n个节点和 k k k条带权路径,要求支持操作:
- 删除最小的带权路径
- 对于给定的节点 x x x,输出所有不经过 x x x的带权路径中的最小值
两种思路,整体二分的待补,线段树维护堆的方法见:[P3250 HNOI2016] 网络 + [NECPC2022] F.Tree Path 树剖+线段树维护堆_HeartFireY的博客-CSDN博客
Code - 树剖+树上差分+整体二分
//待补
Code - 树剖+线段树维护补集
//见:https://blog.csdn.net/yanweiqi1754989931/article/details/125575597
G.Hot Water Pipe
题目分析
给定一段由 n n n段构成的热水管,每一段都有 1 1 1单位的容积,这 n n n段水管从 1 1 1到 n n n从左向右编号,水从左向右流动。初始状态下每段水管 i i i都会有一个温度 a i a_i ai,每分钟温度会下降 1 1 1,当温度下降的 T m i n T_{min} Tmin时会被立即加热到 T m a x T_{max} Tmax。当第 n n n段水管中的用光后,水就会从左向右流动。现在问你间隔一段时间后用水,所取到水的平均温度。
用一个双端队列模拟进水出水过程即可,对于用水量大于总水量的情况单独讨论即可。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e6 + 10;
int a[N];
struct node{
int vol, tem, t;
};
deque<node> q;
inline void solve(){
int n, m, tmin, tmax; cin >> n >> m >> tmin >> tmax;
auto calc = [&](int st, int time, int tem){
time -= st;
if(time < tem - tmin + 1) return tem - time;
(time -= (tem - tmin + 1)) %= (tmax - tmin + 1);
return tmax - time;
};
for(int i = 1, num = 0; i <= n; i++) cin >> num, q.emplace_front(node{
1, num, 0});
int time_cnt = 0;
for(int i = 1; i <= m; i++){
int t, k; cin >> t >> k;
time_cnt += t;
int ans = 0, kk = k;
while(kk && q.size()){
node now = q.front(); q.pop_front();
int nvol = now.vol, ntm = now.tem, nst = now.t;
if(nvol > kk) q.emplace_front(node{
nvol - kk, ntm, nst}), nvol = kk;
kk -= nvol;
ans += nvol * calc(nst, time_cnt, ntm);
}
if(kk) ans += kk * tmax;
cout << ans << endl;
if(i != m) q.emplace_back(node{
k - kk, tmax, time_cnt});
}
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
solve();
return 0;
}
I.Generator
题目分析
初始状态下给定 n n n,每次将 n n n变为 [ 1 , n ] [1, n] [1,n]中的一个数字,经过有限次操作将变为 1 1 1。求变为 1 1 1的操作次数的期望。
设 d p [ n ] dp[n] dp[n]表示当前数字为 n n n,期望 d p [ n ] dp[n] dp[n]次变为 1 1 1。则有转移方程:
d p [ n ] = d p [ 1 ] n + d p [ 2 ] n + ⋯ + d p [ n ] n + 1 dp[n] = \frac{dp[1]}{n} + \frac{dp[2]}{n} + \dots + \frac{dp[n]}{n} + 1 dp[n]=ndp[1]+ndp[2]+⋯+ndp[n]+1
如何理解?当前数字 n n n可以向 [ 1 , n ] [1,n] [1,n]中的任何一个数字转移,转移概率均为 1 n \frac{1}{n} n1,转移占用一步,所以要 + 1 +1 +1。
其中,由于 d p [ 1 ] dp[1] dp[1]表示当前数字为 1 1 1,已经无法再转移,此时操作已经终止。因此期望为 0 0 0即 d p [ 1 ] = 0 dp[1] = 0 dp[1]=0
移项,整理可得:
n d p [ n ] = ∑ i = 1 n d p [ i ] + n ndp[n] = \sum_{i = 1}^{n} dp[i] + n \\ ndp[n]=i=1∑ndp[i]+n
利用错位相减法可以求得 d p [ n ] − d p [ n − 1 ] = 1 n − 1 dp[n] - dp[n - 1] = \frac{1}{n - 1} dp[n]−dp[n−1]=n−11,则可得 d p [ 2 ] = 2 dp[2] = 2 dp[2]=2,则求和式为:
1 + 1 2 + 1 3 + ⋯ + 1 n 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n} 1+21+31+⋯+n1
调和级数求和: 1 + 1 2 + 1 3 + ⋯ + 1 n = ln ( n ) + γ 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n} = \ln(n) + \gamma 1+21+31+⋯+n1=ln(n)+γ,其中 γ \gamma γ为欧拉常数。则对于较大数据可以用该式子求得近似值。
Code
Note: 欧拉常数用Python打表至 1 e 8 1e8 1e8即可。打表程序如下:
import numpy as np
n = 100000000
logn_val = np.log(n)
sum = 0
for i in range(1, n + 1):
sum += (1 / i)
print(sum - logn_val)
AC Code:
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const long double C = 0.5772156599001868;
inline void solve(){
int n = 0; cin >> n, n--;
if(n >= 20000000) cout << log(n) + 1 + C << endl;
else{
long double ans = 1;
for(int i = 1; i <= n; i++) ans += 1.0 / (1.0 * i);
cout << ans << endl;
}
}
signed main(){
cout<<fixed<<setprecision(12);
solve();
return 0;
}
K.Maze
题目分析
给定 n × n n \times n n×n大小迷宫,要求从左上角走到右下角,期间不能经过障碍物,且不能沿同一方向连续行走超过 m m m步。
考虑使用 d i s [ x ] [ y ] [ f a c e ] [ s t e p ] dis[x][y][face][step] dis[x][y][face][step]表示当前在 ( x , y ) (x, y) (x,y)点面向 f a c e face face方向已经连续行走了 s t e p step step步时的最大距离。则可以得到转移方程:
d i s [ x ′ ] [ y ′ ] [ f a c e ′ ] [ s t e p ′ ] = d i s [ x ] [ y ] [ f a c e ] [ s t e p ] + 1 , s . t . s t e p ′ = ( s t e p + 1 ) i f ( f a c e ′ = f a c e ) e l s e ( 1 ) dis[x'][y'][face'][step'] = dis[x][y][face][step] + 1, s.t.step' = (step + 1) if (face' = face)else(1) dis[x′][y′][face′][step′]=dis[x][y][face][step]+1,s.t.step′=(step+1)if(face′=face)else(1)
那么直接 B F S BFS BFS搜索即可。
Code
#include<bits/stdc++.h>
#define int long long
#define mod 998244353
using namespace std;
const int dx[] = {
0 ,0, 1, -1};
const int dy[] = {
1, -1, 0 ,0};
const int INF = 1e9;
const int N = 2e5 + 10;
char g[110][110];
int dis[110][110][4][110], n, m;
struct node{
int x, y, face, step; };
inline int bfs(){
memset(dis, 0x3f, sizeof(dis));
queue<node> q;
q.emplace(node{
1, 1, 0, 0});
for(int i = 0; i < 4; i++) dis[1][1][i][0] = 0;
while(!q.empty()){
node now = q.front(); q.pop();
for(int i = 0; i < 4; i++){
if(now.face != i || now.step <= m){
int nx = now.x + dx[i], ny = now.y + dy[i], nxstep = now.step + 1;
if(now.face != i) nxstep = 1;
if(g[nx][ny] == '*' || nx > n || ny > n || nxstep > m || dis[nx][ny][i][nxstep] < INF) continue;
dis[nx][ny][i][nxstep] = dis[now.x][now.y][now.face][now.step] + 1;
if(nx == n && ny == n) return dis[nx][ny][i][nxstep];
q.emplace(node{
nx, ny, i, nxstep});
//cout << "#DEBUG " << nx << ' ' << ny << ' ' << i << ' ' << nxstep << endl;
}
}
}
return -1;
}
inline void solve(){
cin >> n >> m; getchar();
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
cin >> g[i][j];
}
}
cout << bfs() << endl;
}
signed main(){
int t = 1; cin >> t;
for(int i = 1; i <= 100; i++) g[0][i] = '*';
for(int i = 1; i <= 100; i++) g[i][0] = '*';
while(t--) solve();
return 0;
}
L.Polygon
题目分析
给定 n n n条线段以及每条线段的长度,要求判断能否构成多边形。
考虑多边形构成条件。只需要求边长和然后挨个检验一下就可以了。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 2e5 + 10;
int a[N], sum = 0;
void solve(){
int n = 0; cin >> n; sum = 0;
for(int i = 1; i <= n; i++) cin >> a[i], sum += a[i];
for(int i = 1; i <= n; i++){
if(sum - a[i] <= a[i]){
cout << "NO\n";
return;
}
}
cout << "YES\n";
}
signed main(){
int t = 0; cin >> t;
while(t--) solve();
return 0;
}
边栏推荐
- My understanding of testing (summarized by senior testers)
- 软考中级软件设计师该怎么备考
- I have been doing software testing for three years, and my salary is less than 20K. Today, I put forward my resignation
- Touch and screen automatic rotation debugging
- AMS series - application startup process
- glassfish org. h2.server. Shutdownhandler classnotfoundexception exception exception handling
- asyncio 警告 DeprecationWarning: There is no current event loop
- Summary of the history of Mathematics
- (二)进制
- Illustrated network: what is virtual router redundancy protocol VRRP?
猜你喜欢
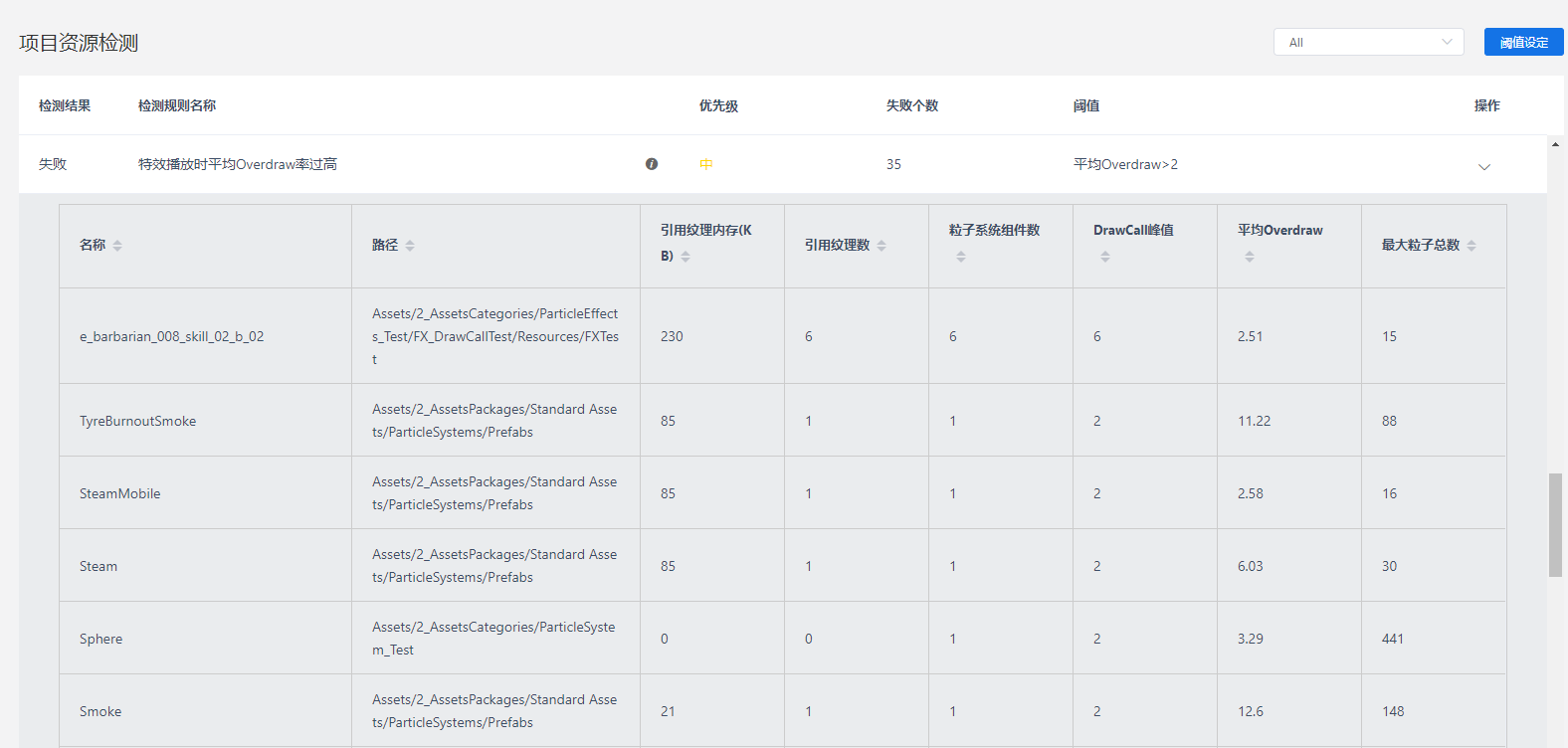
Balance between picture performance of unity mobile game performance optimization spectrum and GPU pressure

ASP.NET-酒店管理系統

栈,单调栈,队列,单调队列

12. Nacos server service registration of source code analysis of Nacos service registration

A simple method of adding dividing lines in recyclerview
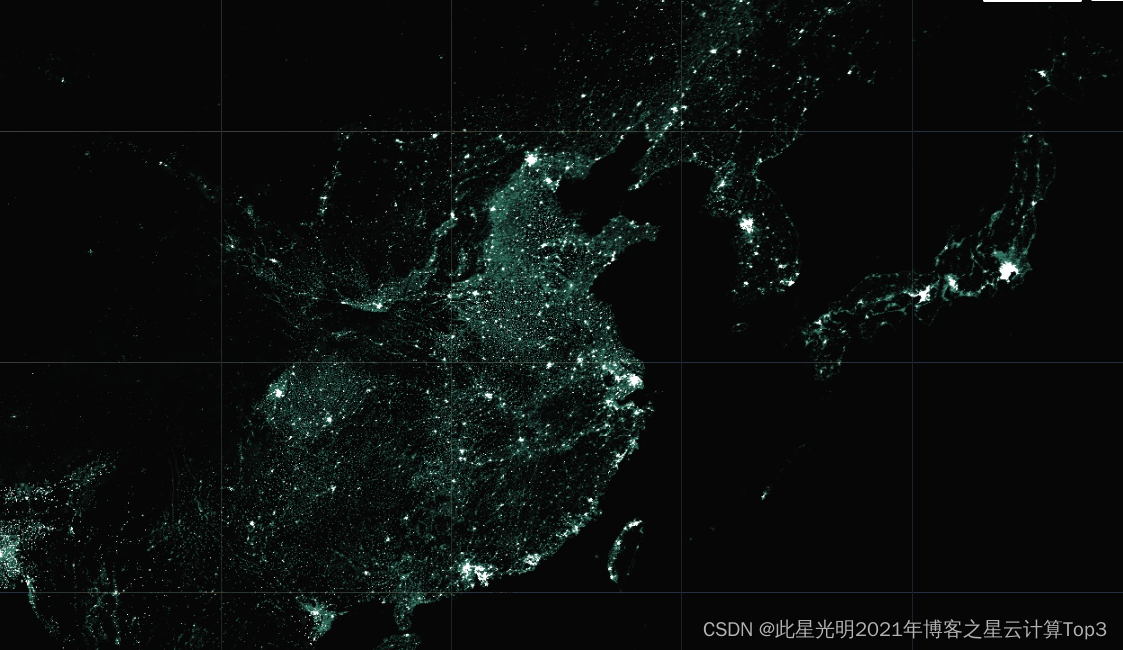
Google Earth engine (GEE) - ghsl global population grid dataset 250 meter resolution
![[proteus simulation] 16 channel water lamp composed of 74hc154 four wire to 12 wire decoder](/img/1f/729594930c7c97d3e731987f4c3645.png)
[proteus simulation] 16 channel water lamp composed of 74hc154 four wire to 12 wire decoder
Lecture 1 number field
I have been doing software testing for three years, and my salary is less than 20K. Today, I put forward my resignation

Unity移动端游戏性能优化简谱之 画面表现与GPU压力的权衡
随机推荐
How to become a senior digital IC Design Engineer (1-3) Verilog coding syntax: Verilog behavior level, register transfer level, gate level (abstract level)
项目管理精华读书笔记(六)
How did I grow up in the past eight years as a test engineer of meituan? I hope technicians can gain something after reading it
One hot code
动态规划(区间dp)
C language two-dimensional array
php如何解决高并发问题
Matlab extracts numerical data from irregular txt files (simple and practical)
行业唯一!法大大电子合同上榜36氪硬核科技企业
Reading notes: heart like Bodhi, Cao Dewang
Solutions of n-ary linear equations and their criteria
[VTK] vtkPolydataToImageStencil 源码解读
2. Hal hardware abstraction layer
程序进程管理工具-go supervisor
Driver development based on I2C protocol
BI技巧丨权限轴
帝国cms 无缩略图 灵动标签(e:loop)判断有无标题图片(titlepic)的两种写法
程序员的创业陷阱:接私活
Commonly used discrete random distribution
Gut | Yu Jun group of the Chinese University of Hong Kong revealed that smoking changes intestinal flora and promotes colorectal cancer (do not smoke)