当前位置:网站首页>多媒体数据处理实验4:LSH索引
多媒体数据处理实验4:LSH索引
2022-08-03 08:47:00 【Polaris_T】
第4次实验: LSH索引
1. 算法描述
功能:
在corel数据集上实现LSH(局部敏感哈希)索引,并对数据集前1000个点分别进行近邻搜索,查找各点的前10个最近邻,并统计搜索算法的性能(准确率、时间)。
2.算法流程:
(1) 确定哈希函数。令 h ( x ) h(x) h(x)表示样本 x x x的哈希变换, x x x与 y y y是两个样本, d ( x , y ) d(x,y) d(x,y)为 x x x与 y y y之间的距离。若 h ( x ) h(x) h(x)满足以下两个条件,则称哈希函数 h ( x ) h(x) h(x)为 ( d 1 , d 2 , p 1 , p 2 ) − s e n s i t i v e (d_1,d_2,p_1,p_2)-sensitive (d1,d2,p1,p2)−sensitive:
若 d ( x , y ) ≤ d 1 ,则 h ( x ) = h ( y ) 的概率至少为 p 1 若 d ( x , y ) ≥ d 2 ,则 h ( x ) = h ( y ) 的概率至多为 p 2 若d(x,y)≤d_1,则h(x)=h(y)的概率至少为p_1 \\ 若d(x,y)≥d_2,则h(x)=h(y)的概率至多为p_2 若d(x,y)≤d1,则h(x)=h(y)的概率至少为p1若d(x,y)≥d2,则h(x)=h(y)的概率至多为p2
在本次实验中,由于我取欧氏距离作为两点之间距离的度量标准,因此我选择 H ( v ) = ⌈ v ⋅ r + b a ⌉ H(v) = \lceil\frac{v·r + b}{a}\rceil H(v)=⌈av⋅r+b⌉作为哈希函数,其中 r r r是一个随机向量, a a a是桶宽, b b b是一个在 [ 0 , a ] [0,a] [0,a]之间均匀分布的随机变量。 v ⋅ r v·r v⋅r可以看做是将 v v v向 r r r上进行投影操作。可以证明 H ( v ) H(v) H(v)是 ( a 2 , 2 a , 1 2 , 1 3 ) (\frac{a}{2},2a,\frac{1}{2},\frac{1}{3}) (2a,2a,21,31)-sensitive的。
(2) 执行哈希映射和分桶策略。对于数据集中的每个点,用一个哈希函数 H i H_i Hi(即选定一组r,b值),将它们全部映射到某个桶 b u c k e t i bucket_i bucketi中。哈希映射的结果即为这些点在该桶中的索引键值。当给定桶数 m m m后,我们可以用按一定方法随机生成的 m m m个哈希函数将这些点映射到 m m m中,并得到这些点在各桶中的索引键值。
(3) 执行检索策略。对于一个给定的查询点 q q q,我们先用上述 m m m个哈希函数将其映射到所有桶中,即得到该点在各桶中的索引键值。然后,我们可以通过这样的方法来确定近邻点的候选集 c a n d i _ s e t candi\_set candi_set:对于第 i ( i = 0 , 1 , . . . , m − 1 ) i(i=0,1,...,m-1) i(i=0,1,...,m−1)号桶,找到在该桶中的索引与点 q q q相同的点,并将这 m m m个桶中找到的所有符合条件的点并起来,构成近邻点候选集。然后,对于候选集,我们通过线性搜索的方法来逐一计算 q q q与 c a n d i _ s e t [ i ] candi\_set[i] candi_set[i]之间的欧氏距离,并最终返回前10个最近邻在原始数据集中的索引号。
(3) 计算准确性。我们可以通过暴力搜索的方法来得到前1000个点各自的10近邻的索引,并将其存放在矩阵中。由于这是一个时间复杂度非常高的过程,因此在第一次计算完毕之后,我就将该矩阵写入了csv文件中,方便下次直接读取调用。对于第 i i i个点,设通过LSH得到的10近邻索引存于列表 p r e d pred pred中,设该点的真实10近邻的索引存于列表 t r u e true true中,那么有:
得到了每个点的TP, TN, FP, FN之后即可利用下面的公式计算出该点的precision, recall, accuracy值:
p r e c i s i o n = T P T P + F P , r e c a l l = T P T P + F N , a c c u r a c y = T P + T N T P + T N + F P + F N precision = \frac{TP}{TP+FP},\ recall = \frac{TP}{TP+FN},\ accuracy = \frac{TP+TN}{TP+TN+FP+FN} precision=TP+FPTP, recall=TP+FNTP, accuracy=TP+TN+FP+FNTP+TN
将1000个点的检索精准率、召回率、准确率取平均即可得到整个实验的最终精准率、召回率、准确率。
3. 核心代码
# 计算欧氏距离
# 不用numba加速,用范数计算快,但用了numba,普通计算更快
@nb.jit(nopython=True)
def calc_dist(x, y):
return np.sqrt(np.sum((x - y) ** 2))
# return np.linalg.norm(x - y)
# R: 32x桶数, b: 1x桶数, a: 标量
# 将向量映射到各桶的索引
def hash_and_fill(inputs, R, b, a):
# 初始化空的hash_table
buckets = [{
} for _ in range(bucket_num)]
mapped_idxes = floor((dot(inputs, R) + b) / a) # 68040x10,每一行是这个点在所有桶中的哈希值
for i, hash_keys in enumerate(mapped_idxes):
for j, hash_key in enumerate(hash_keys):
# 每个桶是一个字典,其中的所有key对应该桶的所有索引键值
buckets[j].setdefault(hash_key, []).append(i)
return buckets # 形如:[{8: [0, 2, 5,...], 12: [2, 12, 16,...] }, {}, {}, ...]
# 并集方法
# 查询与q相似的向量,并输出相似度最高的k个向量在原数据集中的索引
def find(q, k, R, b, a, buckets):
hash_keys = np.floor((dot(q, R) + b) / a)[0] # 不加[0]返回的是1xtables_num的矩阵,取[0]转为数组
# 遍历q点的索引键列表,找各桶中与其索引键值相等的点
for i, hash_key in enumerate(hash_keys):
if i == 0:
candi_set = set(buckets[0][hash_key])
else:
candi_set = candi_set.union(buckets[i][hash_key]) # 候选集
candi_set = list(candi_set) # 转为list便于遍历
dist = [calc_dist(ColorHist[i], q) for i in candi_set]
set_idxes = argsort(dist)[1: k + 1] # set_idxes是近邻点在候选集中的索引,要将其转为在原数据集中的索引
res = [candi_set[i] for i in set_idxes]
return res
# 交集方法
# 查询与q相似的向量,并输出相似度最高的k个向量在原数据集中的索引
def find2(q, k, R, b, a, buckets):
hash_val = np.floor((dot(q, R) + b) / a)[0] # 不加[0]返回的是1xtables_num的矩阵,取[0]转为数组
# 遍历q点的索引键列表,找各桶中与其索引键值相等的点
for i, idx_key in enumerate(hash_val):
if i == 0:
candi_set = set(buckets[0][idx_key])
else:
candi_set = candi_set.intersection(buckets[i][idx_key]) # 候选集
candi_set = list(candi_set) # 转为list便于遍历
dist = [calc_dist(ColorHist[i], q) for i in candi_set]
set_idxes = argsort(dist)[1: k + 1] # set_idxes是近邻点在候选集中的索引,要将其转为在原数据集中的索引
res = [candi_set[i] for i in set_idxes]
return res
4. 实验结果
由于在本次实验中, F N = F P = 10 − T P FN=FP=10-TP FN=FP=10−TP,因此有 p r e c i s i o n = r e c a l l precision=recall precision=recall,且 a c c u r a c y = T P + T N T P + T N + F P + F N = T P + 68040 − 10 − ( 10 − T P ) T P + 68040 − 10 − ( 10 − T P ) + ( 10 − T P ) + ( 10 − T P ) = 2 T P + 68020 68040 ≥ 99.97 accuracy = \frac{TP+TN}{TP+TN+FP+FN}=\frac{TP+68040-10-(10-TP)}{TP+68040-10-(10-TP)+(10-TP)+(10-TP)}=\frac{2TP+68020} {68040} ≥ 99.97% accuracy=TP+TN+FP+FNTP+TN=TP+68040−10−(10−TP)+(10−TP)+(10−TP)TP+68040−10−(10−TP)=680402TP+68020≥99.97,这表明 a c c u r a c y accuracy accuracy一直是一个接近100%的值,我们不能通过 a c c u r a c y accuracy accuracy判断实验结果的好坏。
在本次实验中,我设置了若干组不同的参数,并记录了在不同参数组合下检索前1000个点的10近邻的运行时间和检索精准率(precision),表格如下:
| a = 0.01 | a = 0.03 | a = 0.05 | a = 0.07 | |
|---|---|---|---|---|
| m = 3 | 50s 40.21% | 103s 74.67% | 177s 89.98% | 202s 93.68% |
| m = 5 | 63s 50.09% | 182s 89.72% | 224s 96.46% | 313s 98.92% |
| m = 10 | 138s 76.73% | 288s 97.83% | 375s 99.74% | 476s 99.97% |
| m = 15 | 160s 85.64% | 351s 99.45% | 425s 99.97% | 564s 100.0% |
为了加速计算过程,我采用了numba的@nb.jit(nopython=True)功能。Numba可以将Python函数编译为机器代码(Numba把Python源码通过LLVMPy生成JIT后的.so文件以实现加速),经过Numba编译的Python代码,其运行速度可以接近C或FORTRAN。
对于本实验的距离计算而言,我测试了(1) 使用朴素的平方再开根求距离,(2) 使用np.linalg.norm(x - y)求距离,(3) 使用numba+平方再开根求距离,(4) 使用numba+np.linalg.norm求距离这四种求距离的方法,并且比较了它们求解两点距离的速度,发现使用np.linalg.norm比原始方法快30%,而使用numba加速后计算速度是原始方法的5倍。
使用numba加速后检索前1000个点的10近邻的运行时间和检索精准率(precision)如下:
| a = 0.01 | a = 0.03 | a = 0.05 | a = 0.07 | |
|---|---|---|---|---|
| m = 3 | 8s 37.64% | 24s 74.67% | 24s 88.33% | 36s 95.10% |
| m = 5 | 10s 50.96% | 22s 86.70% | 30s 95.50% | 55s 99.37% |
| m = 10 | 24s 74.67% | 40s 97.10% | 53s 99.74% | 70s 99.96% |
| m = 15 | 34s 85.56% | 58s 99.54% | 69s 99.98% | 73s 100.0% |
边栏推荐
猜你喜欢
随机推荐
开发工具之版本控制
Mysql的in和exists用法区别
Guava的Service
WPS EXCEL 筛选指定长度的文本 内容 字符串
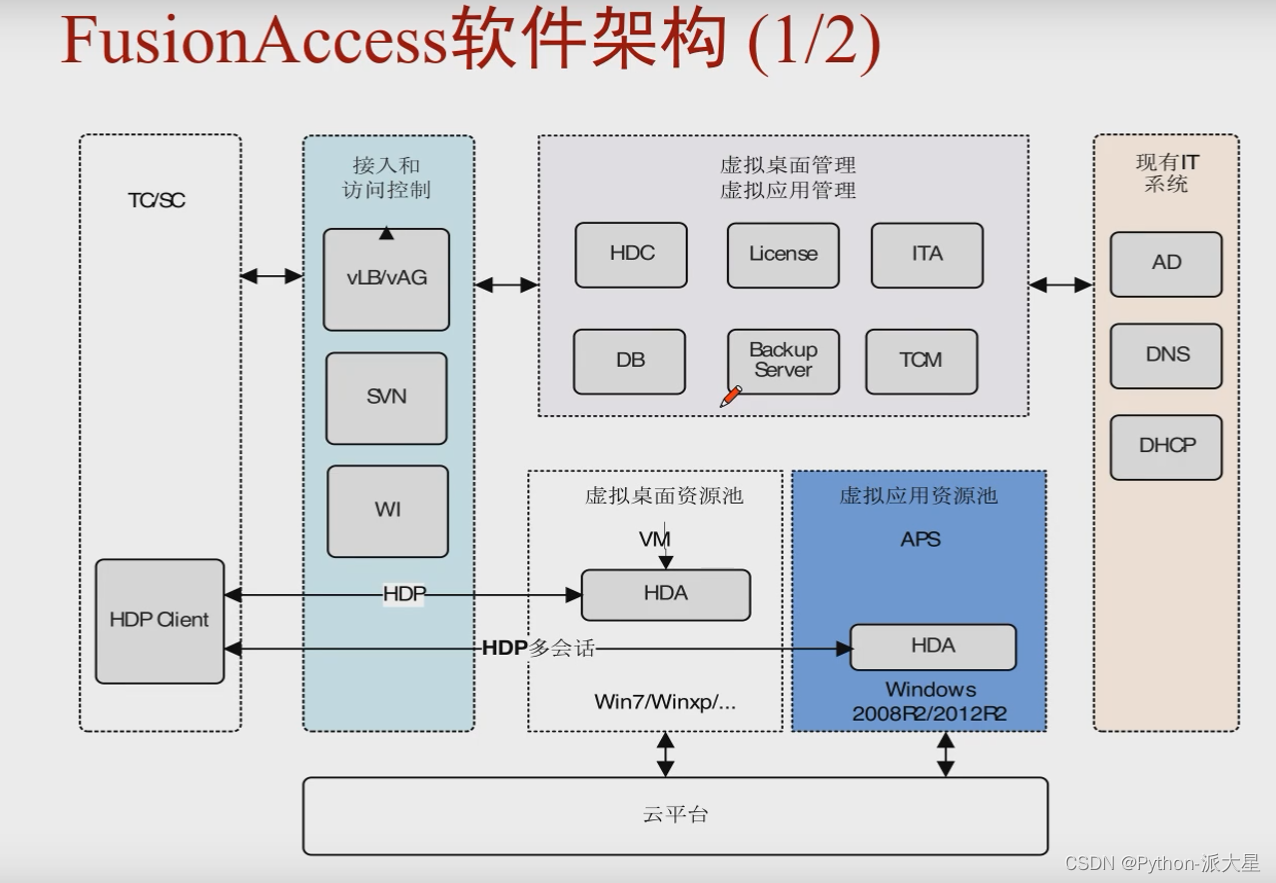
FusionAccess软件架构、FusionAccess必须配置的四个组件、桌面发放流程、虚拟机组类型、桌面组类型
响应式布局经典范例——巨幅背景大标题
HCIP练习(OSPF)
【TPC-DS】25张表的详细介绍,SQL的查询特征
Pop Harmony Basics Big Notes
dflow入门1——HelloWorld!
箭头函数与普通函数的区别
dflow入门4——recurse&reuse&conditional
MySQL数据库————数据库与vs的连接
Industry SaaS Microservice Stability Guarantee Actual Combat
Transformer、BERT、GPT 论文精读笔记
面渣逆袭:MySQL六十六问,两万字+五十图详解
qt使用mysql数据库(自学笔记)
window的供选数据流
用diskpart的offline命令弹出顽固硬盘
编程踩坑合集