【數據挖掘】任務6：DBSCAN聚類

要求

編程實現DBSCAN對下列數據的聚類

數據獲取：https://download.csdn.net/download/qq1198768105/85865302

導庫與全局設置

from scipy.io import loadmat
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import datasets
import pandas as pd

plt.rcParams['font.sans-serif'] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

DBSCAN 聚類參數說明

eps：ϵ-鄰域的距離閾值，和樣本距離超過ϵ的樣本點不在ϵ-鄰域內，默認值是0.5。

min_samples：形成高密度區域的最小點數。作為核心點的話鄰域(即以其為圓心，eps為半徑的圓，含圓上的點)中的最小樣本數(包括點本身)。

若y=-1，則為异常點

由於DBSCAN生成的類別不確定，因此定義一個函數用來篩選出符合指定類別的最合適的參數。

合適的標准是异常點個數最少

def search_best_parameter(N_clusters, X):
    min_outliners = 999
    best_eps = 0
    best_min_samples = 0
    # 迭代不同的eps值
    for eps in np.arange(0.001, 1, 0.05):
        # 迭代不同的min_samples值
        for min_samples in range(2, 10):
            dbscan = DBSCAN(eps=eps, min_samples=min_samples)
            # 模型擬合
            y = dbscan.fit_predict(X)
            # 統計各參數組合下的聚類個數（-1錶示异常點）
            if len(np.argwhere(y == -1)) == 0:
                n_clusters = len(np.unique(y))
            else:
                n_clusters = len(np.unique(y)) - 1
            # 异常點的個數
            outliners = len([i for i in y if i == -1])
            if outliners < min_outliners and n_clusters == N_clusters:
                min_outliners = outliners
                best_eps = eps
                best_min_samples = min_samples
    return best_eps, best_min_samples

# 導入數據
colors = ['green', 'red', 'blue']
smile = loadmat('data-密度聚類/smile.mat')

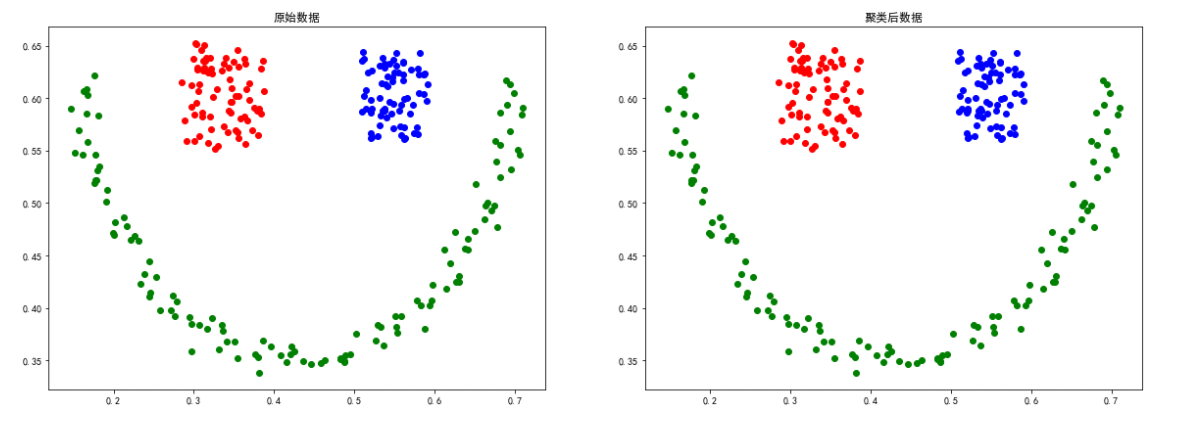
smile數據

X = smile['smile']
eps, min_samples = search_best_parameter(3, X)
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
y = dbscan.fit_predict(X)

# 聚類結果可視化
plt.figure(figsize=(20, 15))
plt.subplot(2, 2, 1)
for i in range(len(smile['smile'])):
    plt.scatter(smile['smile'][i][0], smile['smile'][i][1],
                color=colors[int(smile['smile'][i][2])])
    plt.title("原始數據")
plt.subplot(2, 2, 2)
for i in range(len(y)):
    plt.scatter(smile['smile'][i][0], smile['smile'][i][1], color=colors[y[i]])
    plt.title("聚類後數據")

sizes5數據

# 導入數據
colors = ['blue', 'green', 'red', 'black', 'yellow']
sizes5 = loadmat('data-密度聚類/sizes5.mat')

X = sizes5['sizes5']
eps, min_samples = search_best_parameter(4, X)
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
y = dbscan.fit_predict(X)

# 聚類結果可視化
plt.figure(figsize=(20, 15))
plt.subplot(2, 2, 1)
for i in range(len(sizes5['sizes5'])):
    plt.scatter(sizes5['sizes5'][i][0], sizes5['sizes5']
                [i][1], color=colors[int(sizes5['sizes5'][i][2])])
    plt.title("原始數據")
plt.subplot(2, 2, 2)
for i in range(len(y)):
    if y[i] != -1:
        plt.scatter(sizes5['sizes5'][i][0], sizes5['sizes5']
                    [i][1], color=colors[y[i]])
        plt.title("聚類後數據")

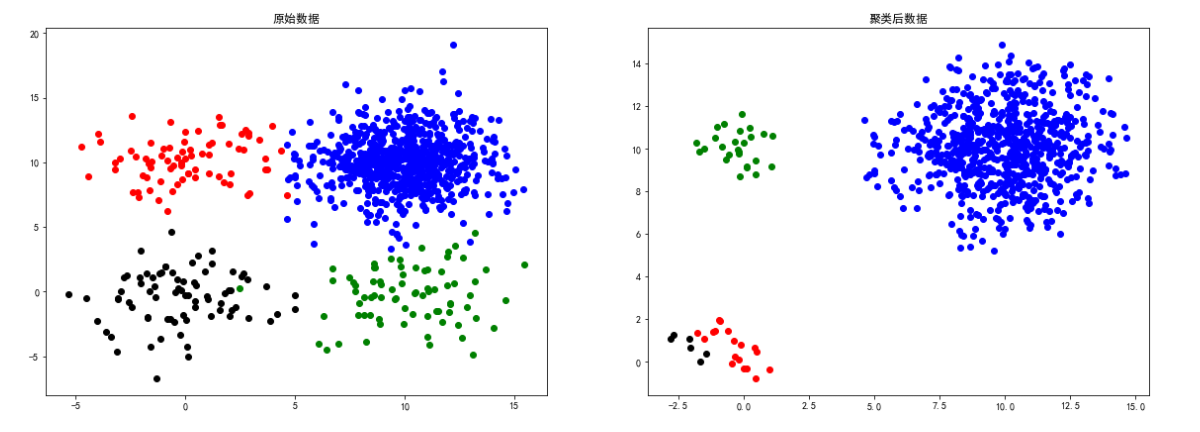
square1數據

# 導入數據
colors = ['green', 'red', 'blue', 'black']
square1 = loadmat('data-密度聚類/square1.mat')

X = square1['square1']
eps, min_samples = search_best_parameter(4, X)
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
y = dbscan.fit_predict(X)

# 聚類結果可視化
plt.figure(figsize=(20, 15))
plt.subplot(2, 2, 1)
for i in range(len(square1['square1'])):
    plt.scatter(square1['square1'][i][0], square1['square1']
                [i][1], color=colors[int(square1['square1'][i][2])])
    plt.title("原始數據")
plt.subplot(2, 2, 2)
for i in range(len(y)):
    plt.scatter(square1['square1'][i][0], square1['square1']
                [i][1], color=colors[y[i]])
    plt.title("聚類後數據")

square4數據

# 導入數據
colors = ['blue', 'green', 'red', 'black',
          'yellow', 'brown', 'orange', 'purple']
square4 = loadmat('data-密度聚類/square4.mat')

X = square4['b']
eps, min_samples = search_best_parameter(5, X)
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
y = dbscan.fit_predict(X)

# 聚類結果可視化
plt.figure(figsize=(20, 15))
plt.subplot(2, 2, 1)
for i in range(len(square4['b'])):
    plt.scatter(square4['b'][i][0], square4['b']
                [i][1], color=colors[int(square4['b'][i][2])])
    plt.title("原始數據")
plt.subplot(2, 2, 2)
for i in range(len(y)):
    plt.scatter(square4['b'][i][0], square4['b']
                [i][1], color=colors[y[i]])
    plt.title("聚類後數據")

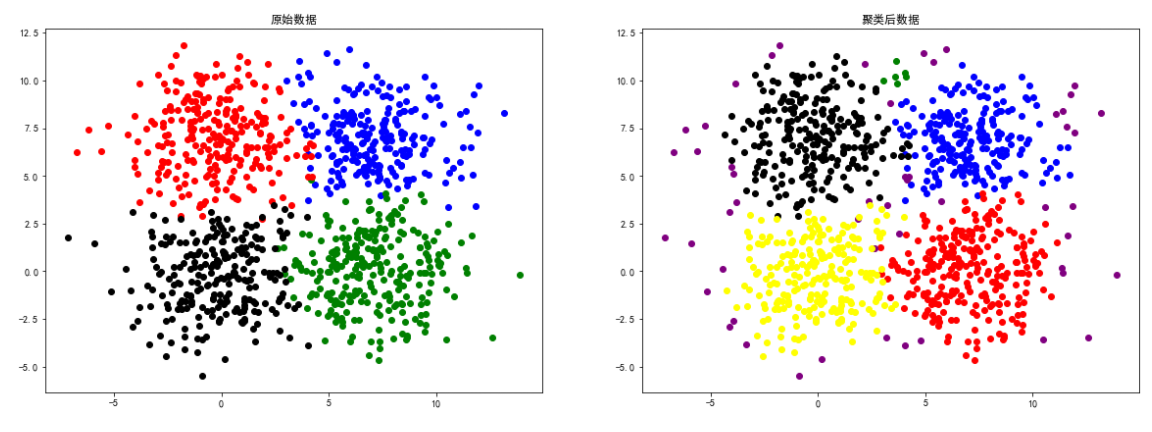
spiral數據

# 導入數據
colors = ['green', 'red']
spiral = loadmat('data-密度聚類/spiral.mat')

X = spiral['spiral']
eps, min_samples = search_best_parameter(2, X)
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
y = dbscan.fit_predict(X)

# 聚類結果可視化
plt.figure(figsize=(20, 15))
plt.subplot(2, 2, 1)
for i in range(len(spiral['spiral'])):
    plt.scatter(spiral['spiral'][i][0], spiral['spiral']
                [i][1], color=colors[int(spiral['spiral'][i][2])])
    plt.title("原始數據")
plt.subplot(2, 2, 2)
for i in range(len(y)):
    plt.scatter(spiral['spiral'][i][0], spiral['spiral']
                [i][1], color=colors[y[i]])
    plt.title("聚類後數據")

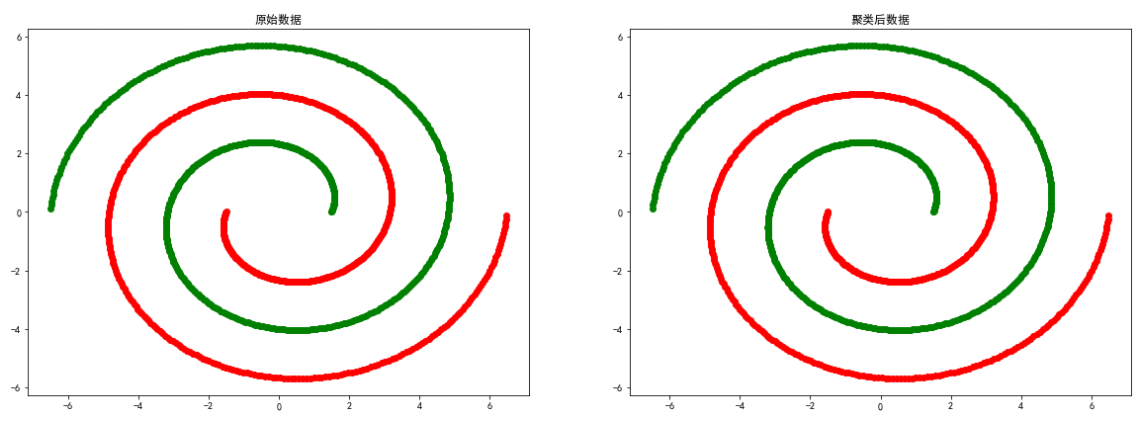
moon數據

# 導入數據
colors = ['green', 'red']
moon = loadmat('data-密度聚類/moon.mat')

X = moon['a']
eps, min_samples = search_best_parameter(2, X)
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
y = dbscan.fit_predict(X)

# 聚類結果可視化
plt.figure(figsize=(20, 15))
plt.subplot(2, 2, 1)
for i in range(len(moon['a'])):
    plt.scatter(moon['a'][i][0], moon['a']
                [i][1], color=colors[int(moon['a'][i][2])])
    plt.title("原始數據")
plt.subplot(2, 2, 2)
for i in range(len(y)):
    plt.scatter(moon['a'][i][0], moon['a']
                [i][1], color=colors[y[i]])
    plt.title("聚類後數據")

long數據

# 導入數據
colors = ['green', 'red']
long = loadmat('data-密度聚類/long.mat')

X = long['long1']
eps, min_samples = search_best_parameter(2, X)
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
y = dbscan.fit_predict(X)

# 聚類結果可視化
plt.figure(figsize=(20, 15))
plt.subplot(2, 2, 1)
for i in range(len(long['long1'])):
    plt.scatter(long['long1'][i][0], long['long1']
                [i][1], color=colors[int(long['long1'][i][2])])
    plt.title("原始數據")
plt.subplot(2, 2, 2)
for i in range(len(y)):
    plt.scatter(long['long1'][i][0], long['long1']
                [i][1], color=colors[y[i]])
    plt.title("聚類後數據")

2d4c數據

# 導入數據
colors = ['green', 'red', 'blue', 'black']
d4c = loadmat('data-密度聚類/2d4c.mat')

X = d4c['a']
eps, min_samples = search_best_parameter(4, X)
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
y = dbscan.fit_predict(X)

# 聚類結果可視化
plt.figure(figsize=(20, 15))
plt.subplot(2, 2, 1)
for i in range(len(d4c['a'])):
    plt.scatter(d4c['a'][i][0], d4c['a']
                [i][1], color=colors[int(d4c['a'][i][2])])
    plt.title("原始數據")
plt.subplot(2, 2, 2)
for i in range(len(y)):
    plt.scatter(d4c['a'][i][0], d4c['a']
                [i][1], color=colors[y[i]])
    plt.title("聚類後數據")

總結

上述實驗證明了DBSCAN聚類方法比較依賴數據點比特置上的關聯度，對於smile、spiral等分布的數據聚類效果較好。