Basis of information entropy

Information entropy

The concept of information entropy is defined by Claude · Shannon On 1948 in . Shannon is a famous American mathematician 、 Founder of information theory , He put forward “ Information entropy ” The concept of , It laid the foundation for information theory and digital communication .

Understand information entropy

Information entropy is a measure of uncertainty , That is, the probability of discrete random time , Simply speaking “ The more chaotic the situation becomes , The greater the entropy of information , On the contrary, the smaller .”

The great mathematician Shannon gave the formula of information entropy , As shown below ：

among , p Means probability , here “X” Represents the set for information entropy calculation . In the decision tree classification algorithm , We can calculate the proportion of each category （ The higher the proportion , The higher the purity of this category ） To understand the , among N Indicates the number of categories , and Pk  Presentation category K Proportion in subset . Understand the above meaning , It is very simple to understand the calculation process of information entropy , Divided into three times and four operations , That is, multiplication 、 Sum and negate .

Information entropy formula calculation

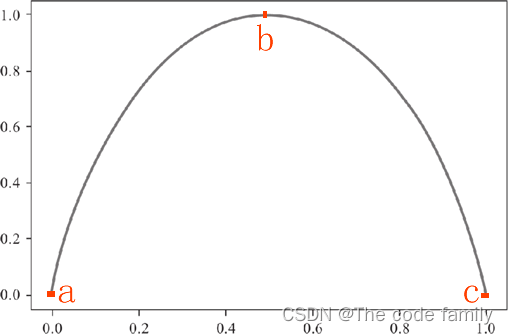
Let's take a simple example , A simple application of the above information entropy calculation formula , stay Binary classification problem in , If all the current samples belong to k Category , Then the proportion of this category in the subset node reaches 100%（ The other category accounts for 0）, namely pk = 1, At this time, the calculation formula of information entropy is as follows ：

The algorithm of logarithmic function will not be repeated here , With 2 Bottom 1 The logarithm of is 0, Therefore, the sum result of the information entropy of the two categories is 0. The entropy of information is 0 Explain that the categories within the subset are consistent “ In order ”. From this we can also know that pk=0.5 When the information entropy reaches the maximum . Based on the above information , We draw Information entropy Function image of , As shown below ：

ID3 Algorithm — Information gain

Through the learning of the previous knowledge , We know that the decision tree algorithm includes all A collection of categories Is the calculation object , And through conditional discrimination , Select the category with high purity , So how do we use information entropy to select decision conditions from feature sets ？ Now let's ID3 The algorithm is illustrated by an example .
ID3（Iterative Dichotomiser 3, Iterative binary tree 3 generation ） Algorithm is one of the decision tree algorithms , It is based on Occam's razor principle Realized , The core idea of this principle is “ The greatest truths are the simplest , Do more with as few things as possible ”.
Apply the above principles to the decision tree , And then there is ID3 The core idea of the algorithm ： A smaller decision tree is better than a larger one , That is, use as few criteria as possible .ID3 The algorithm uses information gain to realize the selection of discrimination conditions , From Shannon's “ Information theory ” We can learn from ,ID3 The algorithm selects the feature dimension with the largest information gain to if -else Distinguish .

1) Understand information gain

In short , Information gain is specific to a specific feature , The presence or absence of a feature is important to the whole system 、 The influence degree of the set can be used as “ Information gain ” To describe . We know , After a if-else After discrimination , The original category set is split into two sets , And our goal is to make a certain category of one set “ The purity ” As high as possible , If the purity of the split subset is higher than that of the original set , That means this is a if-else Division is effective . Made by comparison “ The purity ” The highest division condition , That's what we're looking for “ Most suitable ” The distinguishing condition of the characteristic dimension of .

2) Information gain formula

So how to calculate the information gain value , Here we can use information entropy to calculate . We judge by comparing the information entropy of the set before and after the partition , That is, subtracting , Subtract the information entropy divided according to the attribute of feature dimension from the information entropy of the set before division , Information gain value can be obtained . The formula is as follows ：

 

G(S,a) Represents a collection S Select the feature attribute t To define the information gain of molecular set .H(x) Represents the information entropy of a set . Aforementioned “ Subtract ” It looks a little complicated , Let's focus on the meaning of subtraction ：

• Capital K Express ： By feature dimension t After division , Produced the meaning of several subsets , For example, after the division, there are 5 Subset , that K = 5.
• Lowercase letters k Express ： By feature dimension t After division ,5 A subset of a subset ,k = 1 It refers to the sum calculation starting from the first subset .
• |S| And |Sk|  Express ： aggregate S  The number of elements in , there || Not an absolute value sign , and |Sk| It means after the division , The number of elements in a set .
• |S| /|Sk| Express ： The ratio of the number of elements in a subset to the total number of elements in the original set , It refers to the weight of the subset information entropy , The larger the proportion , The higher the weight .
  Last , Compare the information gain of different feature attributes , The higher the gain value , The higher the purity of the subset , The better the classification , We select the best feature attribute as if-else The best discriminant condition of .