当前位置:网站首页>Linear programming of mathematical modeling (including Matlab code)
Linear programming of mathematical modeling (including Matlab code)
2022-07-03 01:00:00 【Yi EBA】
List of articles
Linear programming of mathematical modeling
1. Linear programming

1.1 matlab The standard form in




>> c = [-2;-3;5]; % Equate to c = [-2,-3,5]'; seek max Take the opposite
>> A = [-2,5,-1;1,3,1]; % inequality
>> b = [-10;12]; % inequality
>> Aeq = [1,1,1]; % equation
>> beq = 7; % equation
>> [x,fval] = linprog(c,A,b,Aeq,beq,zeros(3,1)); % Get results
>> x
x =
6.4286
0.5714
0
>> z = -fval
z =
14.5714
% explain : stay x1 x2 x3 = 6.4286 0.5714 0 Under the circumstances ,maxz = 14.5714

1.2 It can be transformed into a linear programming problem

Example :


Explain : Variable substitution , Turn it into a linear programming model :
c =
1 2 3 4
>> c = [c,c]'
c =
1
2
3
4
1
2
3
4
>> Aeq = [1,-1,-1,1;1,-1,1,-3;1,-1,-2,3]
Aeq =
1 -1 -1 1
1 -1 1 -3
1 -1 -2 3
>> Aeq = [Aeq,-Aeq]
Aeq =
1 -1 -1 1 -1 1 1 -1
1 -1 1 -3 -1 1 -1 3
1 -1 -2 3 -1 1 2 -3
>> beq = [0;1;-1/2]
beq =
0
1.0000
-0.5000
>> [uv,fval] = linprog(c,[],[],Aeq,beq,zeros(8,1));
Optimal solution found.
>> x = uv(1:4) - uv(5:end)
x =
0.2500
0
0
-0.2500
>> minz = fval
minz =
1.2500
>>

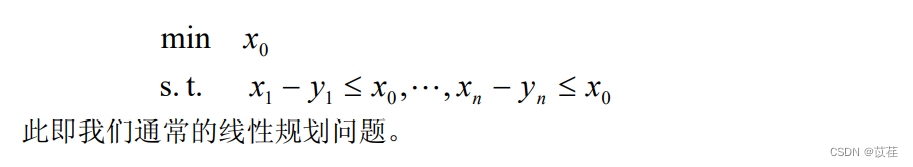
2. Integer programming
The integer of integer programming is only for decision variables , It has nothing to do with whether the optimal solution is an integer .





2.1 Branch and bound algorithm
Usually , Divide all feasible solution spaces into smaller and smaller subsets repeatedly
Set , It's called branching ; And calculate a target lower bound for the solution set in each subset ( For the minimum value problem ), This name
Delimit . After each branch , Those subsets whose bounds exceed the target value of the known feasible solution set will not be further branched , such , Many subsets may be disregarded , This is called pruning . This is the main idea of branch and bound method .
The branch and bound method can be used to solve pure integer or mixed integer programming problems .

2.1.1 Example of branch and bound

>> c = [-3;-2];
>> A = [2,3;2,1];
>> b = [14;9];
>> [x,fval] = linprog(c,A,b,[],[],zeros(2,1));
Optimal solution found.
>> x
x =
3.2500
2.5000
>> z = - fval
z =
14.7500
>>
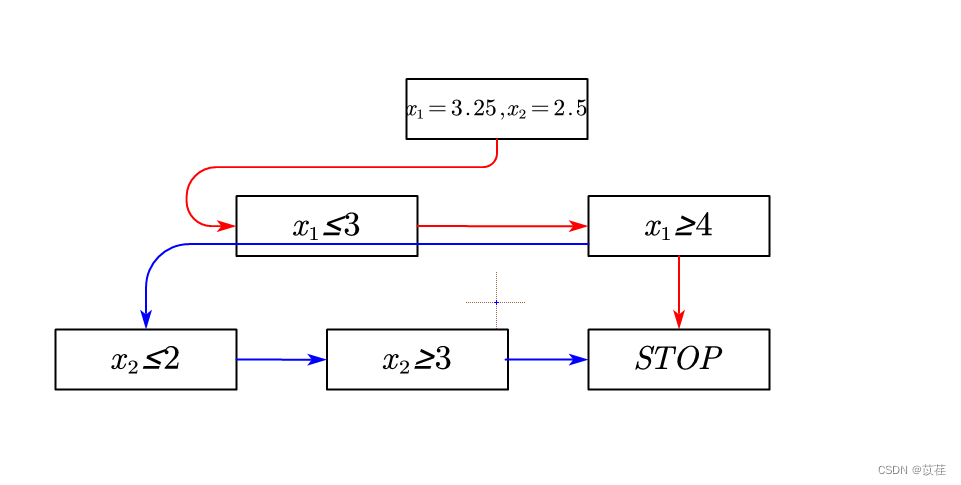
You can see ,x It's not an integer , Next, branch and bound :

>> [x,fval] = linprog(c,A,b,[],[],zeros(2,1),[3,inf]);
Optimal solution found.
>> x
x =
3.0000
2.6667
>> z = -fval
z =
14.3333
>>
Continue to branch and bound :
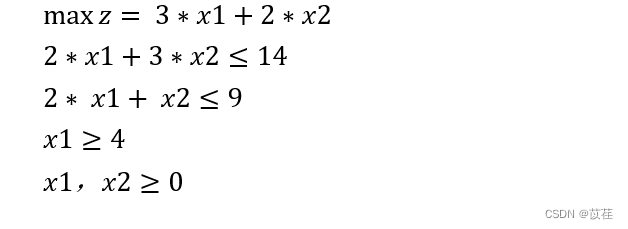
>> [x,fval] = linprog(c,A,b,[],[],[4,0]);
Optimal solution found.
>> x
x =
4.0000
1.0000
>> z = -fval
z =
14.0000
14.3333 Than 14.0000 Big , So in x1≤3 Next, branch and bound :
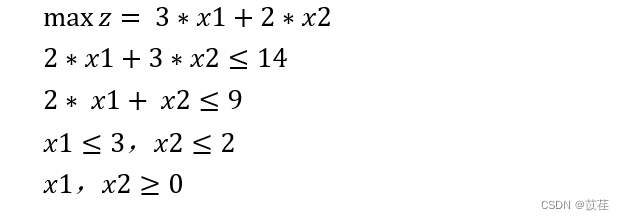
>> [x,fval] = linprog(c,A,b,[],[],zeros(2,1),[3,2]);
Optimal solution found.
>> x
x =
3
2
>> z = -fval
z =
13
>>
Continue to branch and bound :
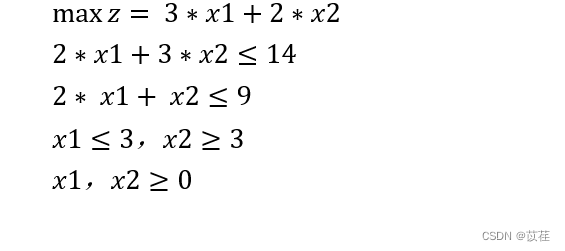
>> [x,fval] = linprog(c,A,b,[],[],[0,3],[3,inf]);
Optimal solution found.
>> x
x =
2.5000
3.0000
>> z = -fval
z =
13.5000
>>
So the optimal solution of integer programming is 14.
2.1.2 matlab Code implementation
branchbound.m
function [newx,newfval,status,newbound] = branchbound(f,A,B,I,x,fval,bound,Aeq,Beq,lb,ub,e)
% Branch and bound method to solve integer programming
% f,A,B,Aeq,Beq,lb,ub Same as linear programming
% I A vector that limits variables to integers
% x Is the initial solution ,fval For the initial value
options = optimset('display','off');
[x0,fval0,status0]=linprog(f,A,B,Aeq,Beq,lb,ub,[],options);
% Final exit condition in recursion
% If there is no solution or the solution is larger than the existing upper bound, the original solution is returned
if status0 <= 0 || fval0 >= bound
newx = x;
newfval = fval;
newbound = bound;
status = status0;
return;
end
% Whether it is an integer solution , If it is an integer solution, it returns
intindex = find(abs(x0(I) - round(x0(I))) > e);
if isempty(intindex) % Judge whether it is a null value
newx(I) = round(x0(I));
newfval = fval0;
newbound = fval0;
status = 1;
return;
end
% When there is a non integral feasible solution , Then branch solution
% At this point, there must be an integer solution or an empty solution
% Find the first variable that does not meet the integer requirements
n = I(intindex(1));
addA = zeros(1,length(f));
addA(n) = 1;
% Construct the first branch x<=floor(x(n))
A = [A;addA];
B = [B,floor(x(n))];% Rounding down
[x1,fval1,status1,bound1] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);
A(end,:) = [];
B(:,end) = [];
% The first branch of the solution , If it is a better solution, replace , If not, leave it as it is
status = status1;
if status1 > 0 && bound1 < bound
newx = x1;
newfval = fval1;
bound = fval1;
newbound = bound1;
else
newx = x0;
newfval = fval0;
newbound = bound;
end
% Construct the second branch
A = [A;-addA];
B = [B,-ceil(x(n))];% Rounding up
[x2,fval2,status2,bound2] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);
A(end,:) = [];
B(:,end) = [];
% The second branch of the solution , And compare it with the first branch , If better, replace
if status2 > 0 && bound2 < bound
status = status2;
newx = x2;
newfval = fval2;
newbound = bound2;
end
intprog.m
function [x,fval,status] = intprog(f,A,B,I,Aeq,Beq,lb,ub,e)
% Integer programming solving function intprog()
% among f Is the objective function vector
% A and B For inequality constraints Aeq And Beq For equality constraints
% I Is an integer constraint
% lb And ub They are the lower bound and upper bound of variables
% x For the best solution ,fval Is the optimal value
% Example :
% maximize 20 x1 + 10 x2
% S.T.
% 5 x1 + 4 x2 <=24
% 2 x1 + 5 x2 <=13
% x1, x2 >=0
% x1, x2 Is an integer
% f=[-20, -10];
% A=[ 5 4; 2 5];
% B=[24; 13];
% lb=[0 0];
% ub=[inf inf];
% I=[1,2];
% e=0.000001;
% [x v s]= IP(f,A,B,I,[],[],lb,ub,,e)
% x = 4 1 v = -90.0000 s = 1
% Control input parameters
if nargin < 9, e = 0.00001;
if nargin < 8, ub = [];
if nargin < 7, lb = [];
if nargin < 6, Beq = [];
if nargin < 5, Aeq = [];
if nargin < 4, I = [1:length(f)];
end, end, end, end, end, end
% Solve the linear programming corresponding to integer programming , Judge whether there is a solution
options = optimset('display','off');
[x0,fval0,exitflag] = linprog(f,A,B,Aeq,Beq,lb,ub,[],options);
if exitflag < 0
disp(' There is no suitable integer solution ');
x = x0;
fval = fval0;
status = exitflag;
return;
else
% The branch and bound method is used to solve
bound = inf;
[x,fval,status] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);
end
Branch and bound process :
2.1.3 intlinprog Function to solve integer programming

>> c = [-40;-90];
>> A = [9,7;7,20];
>> b = [56;70];
>> [x,fval] = intlinprog(c,[1 2],A,b,[],[],zeros(2,1));
>> x
x =
4.0000
2.0000
>> -fval
ans =
340

x = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub): Compared to the function linprog One more parameter intcon, Used to calibrate the position of integer variables :x1、x2 Integers , namely intcon = [1 2].
2.2 Cut plane algorithm
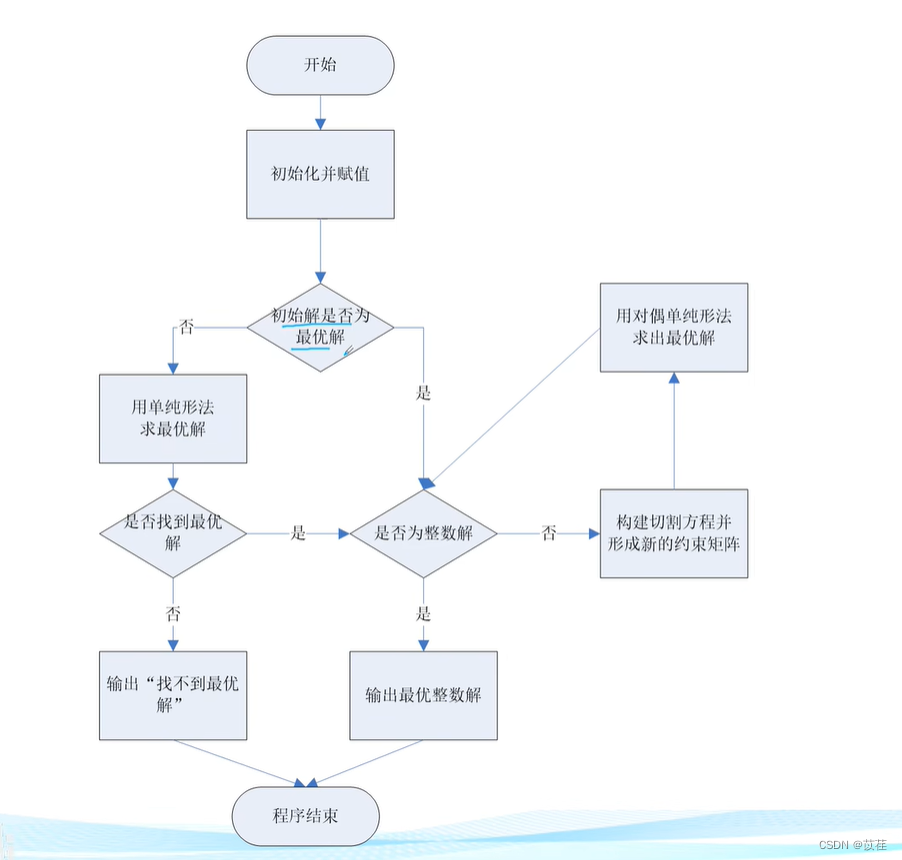

Explain : Two inequalities , Here we introduce two relaxation variables x3 and x4;

2.2.1 matlab Implementation code
function [intx,intf] = DividePlane(A,c,b,baseVector)
% function : Solve integer programming by cutting plane method
% Invocation format :[intx,intf]=DividePlane(A,c,b,baseVector)
% among , A: Constraint matrix ;
% c: Objective function coefficient vector ;
% b: Constrain the right vector ;
% baseVector: Initial basis vector ;
% intx: The independent variable value when the objective function takes the maximum value ;
% intf: The maximum value of the objective function ;
sz = size(A);
nVia = sz(2);% Get how many decision variables
n = sz(1);% Get how many constraints
xx = 1:nVia;
if length(baseVector) ~= n
disp(' The number of base variables should be equal to the number of rows of the constraint matrix !');
mx = NaN;
mf = NaN;
return;
end
M = 0;
sigma = -[transpose(c) zeros(1,(nVia-length(c)))];
xb = b;
% First, use the simplex method to find the optimal solution
while 1
[maxs,ind] = max(sigma);
%-------------------- Use the simplex method to find the optimal solution --------------------------------------
if maxs <= 0 % When the inspection numbers are less than 0 when , Find the optimal solution .
vr = find(c~=0 ,1,'last');
for l=1:vr
ele = find(baseVector == l,1);
if(isempty(ele))
mx(l) = 0;
else
mx(l)=xb(ele);
end
end
if max(abs(round(mx) - mx))<1.0e-7 % Determine whether the optimal solution is an integer solution , If it's an integer solution .
intx = mx;
intf = mx*c;
return;
else % If the optimal solution is not an integer solution , Construction of cutting equation
sz = size(A);
sr = sz(1);
sc = sz(2);
[max_x, index_x] = max(abs(round(mx) - mx));
[isB, num] = find(index_x == baseVector);
fi = xb(num) - floor(xb(num));
for i=1:(index_x-1)
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
for i=(index_x+1):sc
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
Atmp(1,index_x) = 0; % Construct the initial table of dual simplex method
A = [A zeros(sr,1);-Atmp(1,:) 1];
xb = [xb;-fi];
baseVector = [baseVector sc+1];
sigma = [sigma 0];
%------------------- Iterative process of dual simplex method ----------------------
while 1
%----------------------------------------------------------
if xb >= 0 % Judge if the right end vectors are greater than 0, Find the optimal solution
if max(abs(round(xb) - xb))<1.0e-7 % If the integer solution is obtained by the dual simplex method , Then the optimal integer solution is returned
vr = find(c~=0 ,1,'last');
for l=1:vr
ele = find(baseVector == l,1);
if(isempty(ele))
mx_1(l) = 0;
else
mx_1(l)=xb(ele);
end
end
intx = mx_1;
intf = mx_1*c;
return;
else % If the optimal solution obtained by the dual simplex method is not an integer solution , Continue to add cutting equations
sz = size(A);
sr = sz(1);
sc = sz(2);
[max_x, index_x] = max(abs(round(mx_1) - mx_1));
[isB, num] = find(index_x == baseVector);
fi = xb(num) - floor(xb(num));
for i=1:(index_x-1)
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
for i=(index_x+1):sc
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
Atmp(1,index_x) = 0; % The initial table of the next dual simplex iteration
A = [A zeros(sr,1);-Atmp(1,:) 1];
xb = [xb;-fi];
baseVector = [baseVector sc+1];
sigma = [sigma 0];
continue;
end
else % If the right vector is not all greater than 0, Then carry out the process of changing base variables of dual simplex method
minb_1 = inf;
chagB_1 = inf;
sA = size(A);
[br,idb] = min(xb);
for j=1:sA(2)
if A(idb,j)<0
bm = sigma(j)/A(idb,j);
if bm<minb_1
minb_1 = bm;
chagB_1 = j;
end
end
end
sigma = sigma -A(idb,:)*minb_1;
xb(idb) = xb(idb)/A(idb,chagB_1);
A(idb,:) = A(idb,:)/A(idb,chagB_1);
for i =1:sA(1)
if i ~= idb
xb(i) = xb(i)-A(i,chagB_1)*xb(idb);
A(i,:) = A(i,:) - A(i,chagB_1)*A(idb,:);
end
end
baseVector(idb) = chagB_1;
end
%------------------------------------------------------------
end
%-------------------- Iterative process of dual simplex method ---------------------
end
else % If the inspection number is not less than 0 Of , Then carry out the iteration process of simplex algorithm
minb = inf;
chagB = inf;
for j=1:n
if A(j,ind)>0
bz = xb(j)/A(j,ind);
if bz<minb
minb = bz;
chagB = j;
end
end
end
sigma = sigma -A(chagB,:)*maxs/A(chagB,ind);
xb(chagB) = xb(chagB)/A(chagB,ind);
A(chagB,:) = A(chagB,:)/A(chagB,ind);
for i =1:n
if i ~= chagB
xb(i) = xb(i)-A(i,ind)*xb(chagB);
A(i,:) = A(i,:) - A(i,ind)*A(chagB,:);
end
end
baseVector(chagB) = ind;
end
M = M + 1;
if (M == 1000000)
disp(' No optimal solution found !');
mx = NaN;
minf = NaN;
return;
end
end
2.2.2 Application of cutting plane algorithm

>> c = [-1;-1]; % Do not add slack variables
>> A = [-1 1 1 0;3 1 0 1]; % Add the relaxation variable
>> b = [1;4];
>> [x fval] = DividePlane(A,c,b,[3 4]); % Relax variables 3 4
>> x
x =
1.0000 1.0000
>> maxz = -fval
maxz =
2
>>
2.3 hungarian algorithm (0-1 planning )
0-1 The planning problem can also be seen as an interval [0,1] Integer programming of , The following use intlinprog Function to calculate :

>> c = [-3 2 -5]';
>> A = [1 2 -1;1 4 1];
>> b = [2;4];
>> c = [-3 2 -5]';
>> A = [1 2 -1;1 4 1;1 1 0;0 4 1];
>> b = [2;4;3;6];
>> [x fval] = intlinprog(c,[1 2 3],A,b,[],[],zeros(3,1),ones(3,1));
>> x
x =
1
0
1
>> maxz = -fval
maxz =
8
>>
Hungarian algorithm solves 0-1 Programming problem :
2.3.1 Investment issues

2.3.2 Mutually exclusive constraint problem


2.3.3 Fixed cost problem

2.3.4 Assignment problem

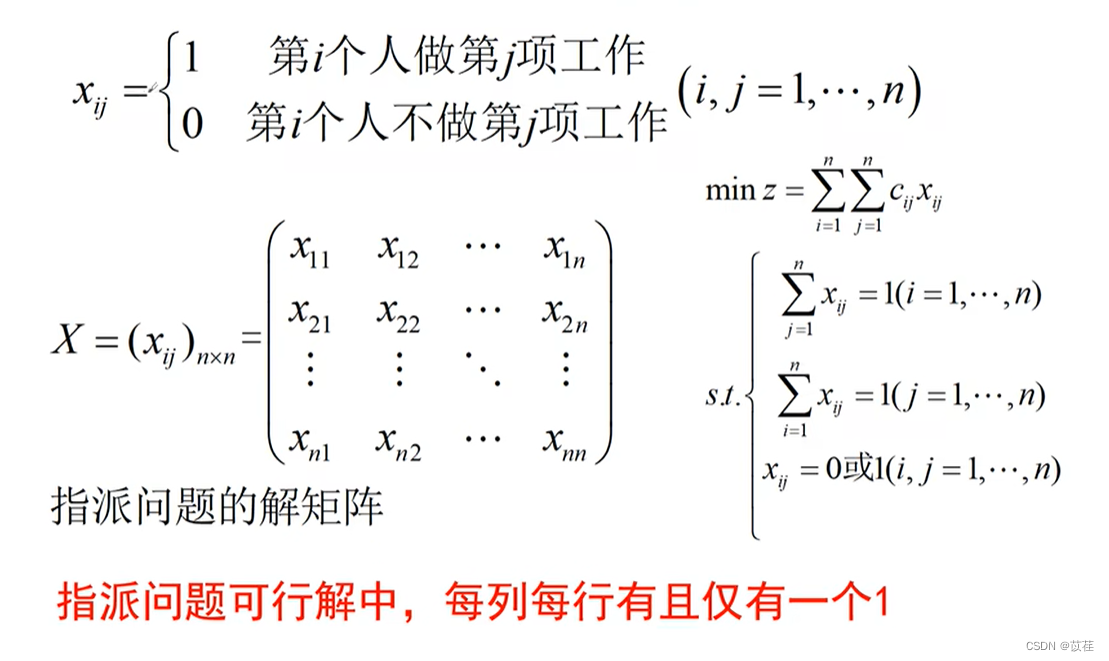
give an example
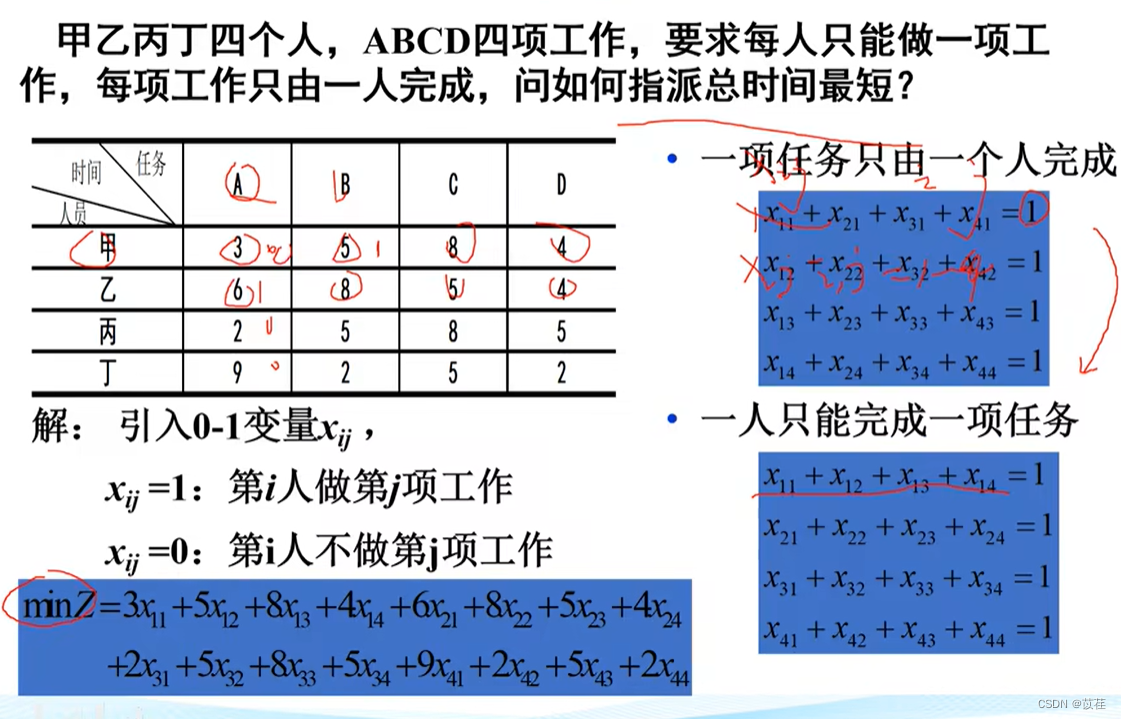
2.3.5 Nonstandard assignment problem

2.3.6 Hungarian algorithm description




Find the minimum value in each line and subtract the minimum value from each element of the line , Find the minimum value in each column and subtract the minimum value from each element of the column , From only one 0 The line of the element begins , take 0 Element circle , Cross out this 0 Other elements in the column 0 Elements , Then look for only one 0 The row of the element , Repeat , In the business 0 When there is no element , There is only one 0 Columns of elements , loops , Cross out this 0 Other elements on the line 0 Elements .
Last , If circled 0 The number of elements is less than the order n, Do the following :( Otherwise, find the solution )
Yes, there is no circle 0 The line type of elements √, Duel √ Cross out all in the line of 0 The column of the element is marked with √, Duel √ Columns of contain circles 0 The line of the element is marked √, Repeat the above 3 Step , Until we don't get a new hit √ The line of No .
below , Yes, No √ Draw a horizontal line on the line , Duel √ Draw a vertical line on the column , So as to cover all 0 The minimum number of horizontal lines of an element , It should be equal to circle 0 Number of elements , Then proceed as follows , Transform the current matrix to increase 0 Elements , In order to find n Independent 0 Elements :
Find the minimum element value of all elements not covered by the line , Will hit √ Subtract the minimum element value from each line of , hit √ Add the minimum element value to each column of , Thus a new assignment matrix is obtained , Repeat the above with this new assignment matrix All steps , Until we find out n Independent 0 Element results .
Example
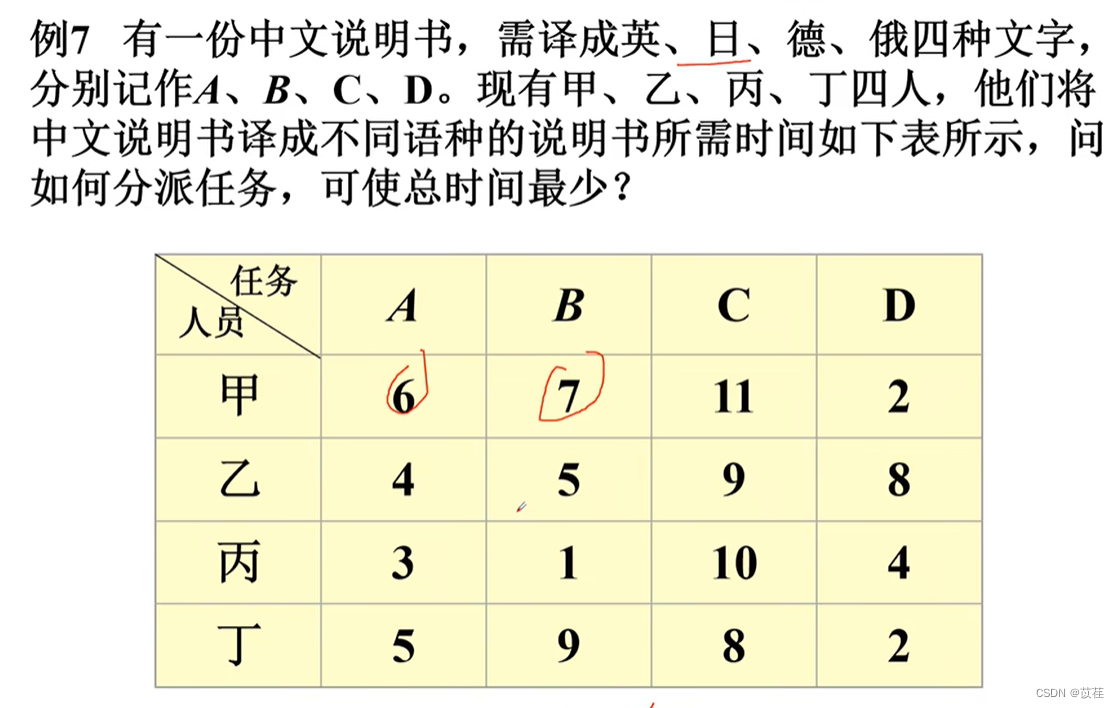
Implementation steps
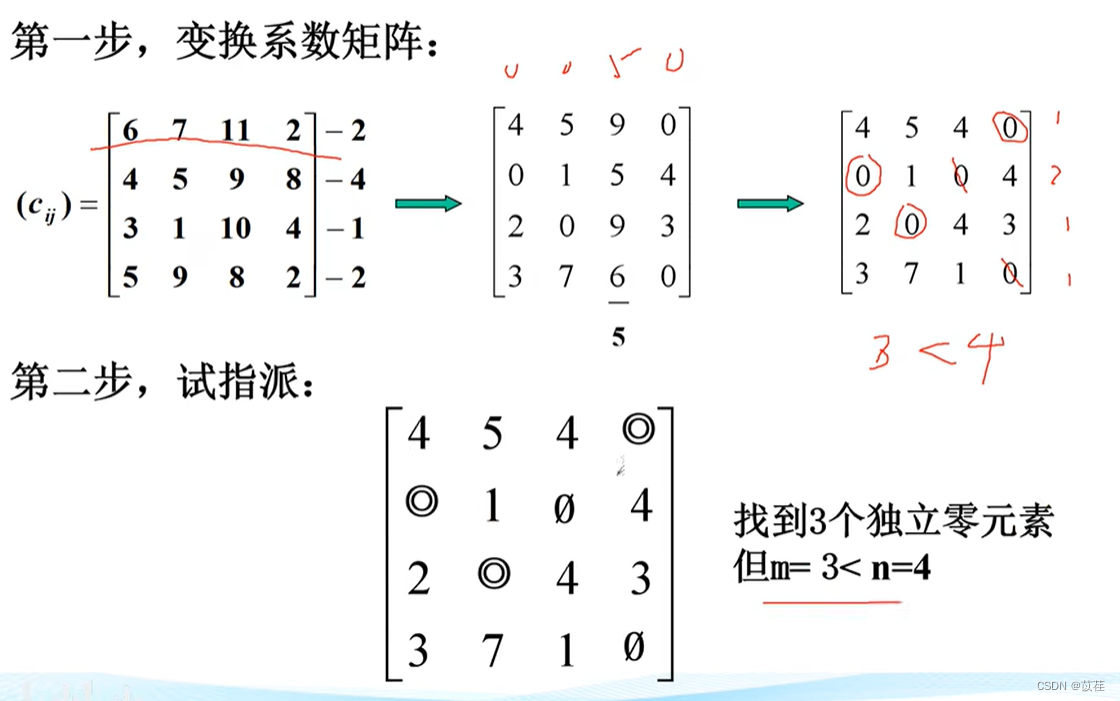
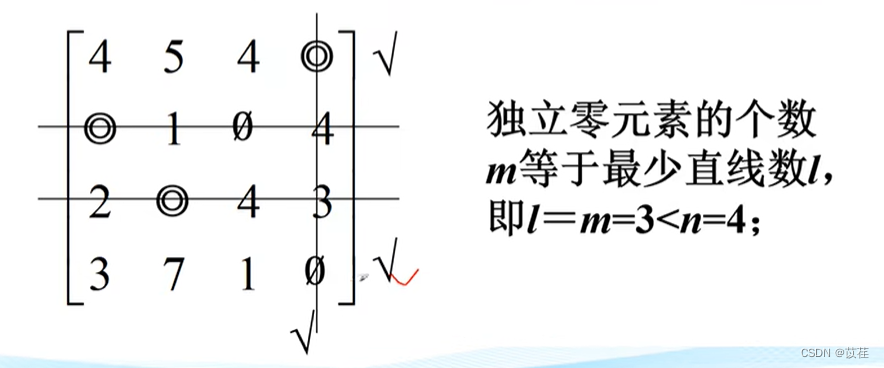
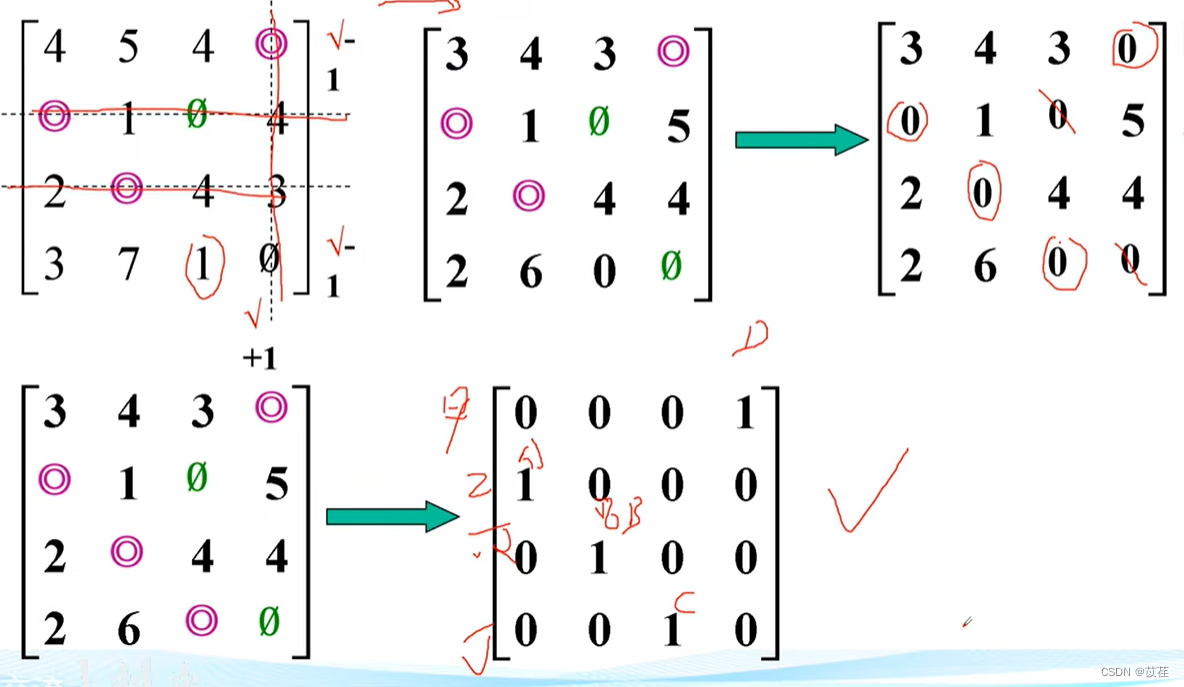
2.3.7 Hungarian algorithm code implementation
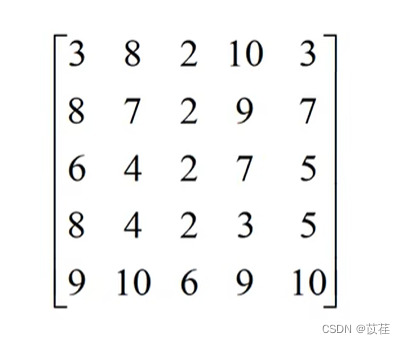
>> c = [3 8 2 10 3;8 7 2 9 7;6 4 2 7 5;8 4 2 3 5;9 10 6 9 10]
c =
3 8 2 10 3
8 7 2 9 7
6 4 2 7 5
8 4 2 3 5
9 10 6 9 10
>> c = c(:); % A matrix is converted into a vector
>> a = zeros(10,25);
>> for i = 1:5
a(i,(i-1)*5+1:5*i) = 1;
a(5+i,i:5:25) = 1;
end % Loop transforms assignment problem into linear programming problem
>> b = ones(10,1); % 10 A constraint (5*2)
>> [x y] = linprog(c,[],[],a,b,zeros(25,1),ones(25,1));
Optimal solution found.
>> X = reshape(x,5,5)
X =
0 0 0 0 1
0 0 1 0 0
0 1 0 0 0
0 0 0 1 0
1 0 0 0 0
>> opt = y
opt =
21
>>
>> [x y] = linprog(-c,[],[],a,b,zeros(25,1),ones(25,1));
Optimal solution found.
>> X = reshape(x,5,5)
X =
0 1 0 0 0
0 0 0 1 0
0 0 1 0 0
1 0 0 0 0
0 0 0 0 1
>> opt = -y
opt =
37
>>

>> c = [6 7 11 2;4 5 9 8;3 1 10 4;5 9 8 2];
>> a = zeros(8,16);
>> for i = 1:4
a(i,(i-1)*4+1:4*i) = 1;
a(4+i,i:4:16) = 1;
end
>> b = ones(8,1);
>> [x y] = linprog(c,[],[],a,b,zeros(16,1),ones(16,1));
Optimal solution found.
>> X = reshape(x,4,4)
X =
0 0 0 1
1 0 0 0
0 1 0 0
0 0 1 0
>> opt = y
opt =
15
>>
>> [x y]= linprog(-c,[],[],a,b,zeros(25,1),ones(25,1));
Optimal solution found.
>> X = reshape(x,5,5)
X =
0 1 0 0 0
0 0 0 1 0
0 0 1 0 0
1 0 0 0 0
0 0 0 0 1
>> opt = -y
opt =
37
>>

>> c = [6 7 11 2;4 5 9 8;3 1 10 4;5 9 8 2];
>> a = zeros(8,16);
>> for i = 1:4
a(i,(i-1)*4+1:4*i) = 1;
a(4+i,i:4:16) = 1;
end
>> b = ones(8,1);
>> [x y] = linprog(c,[],[],a,b,zeros(16,1),ones(16,1));
Optimal solution found.
>> X = reshape(x,4,4)
X =
0 0 0 1
1 0 0 0
0 1 0 0
0 0 1 0
>> opt = y
opt =
15
>>
3. Reference material
《 Mathematical modeling algorithm and Application 》( Si keeping )《 Mathematical modeling algorithm and application problem solving 》( Si keeping )- >> bilibili Mathematical modeling learning tutorial
边栏推荐
- Meaning of Tencent cloud free SSL certificate extension file
- 拥抱平台化交付的安全理念
- leetcode-2280:表示一个折线图的最少线段数
- [Luogu p4320] road meets (round square tree)
- [introduction to AUTOSAR seven tool chain]
- Vulkan is not a "panacea"“
- 2022中国3D视觉企业(引导定位、分拣场景)厂商名单
- Advanced pointer (I)
- cordova-plugin-device获取设备信息插件导致华为审核不通过
- [love crash] neglected details of gibaro
猜你喜欢
【AutoSAR 六 描述文件】
[AUTOSAR five methodology]

RISA rz/g2l processor introduction | frame diagram | power consumption | schematic diagram and hardware design guide

Thank you for being together for these extraordinary two years!
Vulkan practice first bullet
![[AUTOSAR nine c/s principle Architecture]](/img/59/ce32c0ff58ef5d8385fe950136175b.png)
[AUTOSAR nine c/s principle Architecture]
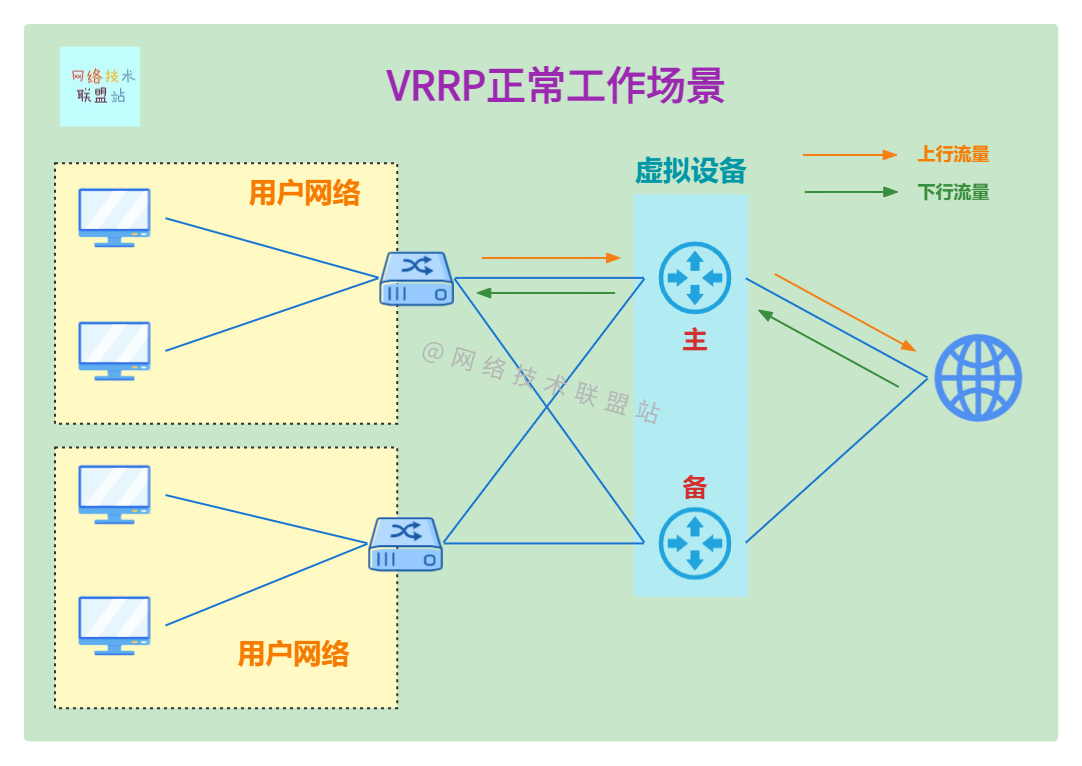
图解网络:什么是虚拟路由器冗余协议 VRRP?

【AutoSAR 七 工具链简介】

百度智能云牵头打造智能云综合标准化平台

Deep analysis of data storage in memory
随机推荐
[daily training] 871 Minimum refueling times
Set up nacos2 X cluster steps and problems encountered
Thread start and priority
1.12 - Instructions
[introduction to AUTOSAR seven tool chain]
tail -f 、tail -F、tailf的区别
How to convert Quanzhi a40i/t3 to can through SPI
What is needed to develop a domestic arm intelligent edge computing gateway
12_微信小程序之微信视频号滚动自动播放视频效果实现
Array and collection performance comparison
瑞萨RZ/G2L ARM开发板存储读写速度与网络实测
Unity learns from spaceshooter to record the difference between fixedupdate and update in unity for the second time
Tensorflow 2.x(keras)源码详解之第十五章:迁移学习与微调
Leetcode-871: minimum refueling times
About qbytearray storage hexadecimal and hexadecimal conversion
Arduino开发之按键检测与正弦信号输出
Use Jenkins II job
2022 list of manufacturers of Chinese 3D vision enterprises (guided positioning and sorting scenes)
1038 Recover the Smallest Number
图解网络:什么是虚拟路由器冗余协议 VRRP?
![[AUTOSAR five methodology]](/img/75/ce28bd8a16bbefa94c88376170c832)