Theoretical description of linear equations and summary of methods for solving linear equations by eigen

1. System of linear equations ( matrix equation ) theory

A system of linear equations is a system of equations in which each equation is linear with respect to an unknown quantity , The equation is expressed as follows ：

$$\{\begin{array}{c}{a}_1{x}_1+b_1{x}_2+c_1{x}_3=d_1\\ a_2{x}_1+b_2{x}_2+c_2{x}_3=d_2\\ a_3{x}_1+b_3{x}_2+c_3{x}_3=d_3\end{array}$$
Write the thread equation in matrix form as follows ：
$$Ax=b$$
among ,
$$A=\left(\begin{array}{ccc}{a}_1& b_1& c_1\\ a_2& b_2& c_2\\ a_3& b_3& c_3\end{array}\right),x=\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right),d=\left(\begin{array}{c}{d}_1\\ d_2\\ d_3\end{array}\right)$$

Eigen Provides a wealth of linear equation solving methods , Include LU Decomposition ,QR Decomposition ,SVD（ Singular value decomposition ）、 Eigenvalue decomposition and other basis A Type of matrix 、 Requirements for accuracy of results and calculation speed , You can choose different calculation methods , Let's introduce one by one .

The picture below is Eigen Introduction of some decomposition methods .

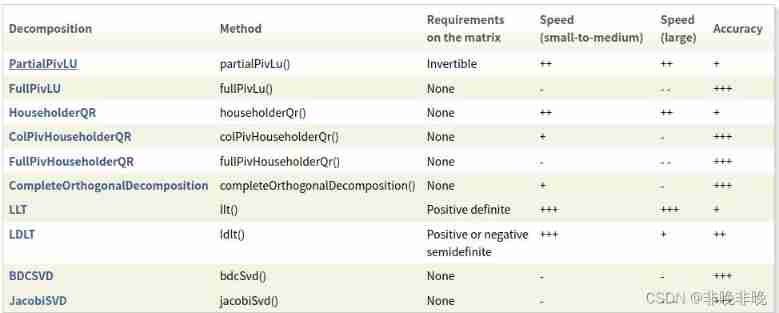
If you know matrix well , Then you can easily choose a reasonable solution , For example, if the matrix A Is a full rank and asymmetric matrix , Then you can choose PartialPivLU Solution , If you know that your matrix is symmetric positive definite , So choose LLT perhaps LDLT Decomposition is a good choice . The following figure shows the speed of some solutions .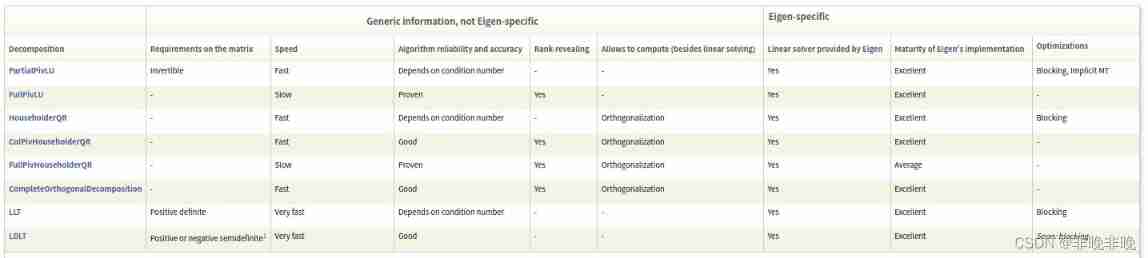

2. QR decompose

QR（ Orthogonal triangle ） The decomposition method is the most effective and widely used method for finding all eigenvalues of a general matrix , A general matrix is first transformed by orthogonal similarity into Hessenberg matrix , And then apply QR Methods to find eigenvalues and eigenvectors . It decomposes the matrix into a normal orthogonal matrix Q And the upper triangular matrix R, So called QR Decomposition , And the general symbol of this normal orthogonal matrix Q of .

$$A=QR$$
among Q It's an orthogonal matrix （ Or unitary matrix ）, namely $Q{Q}^T=1$,$R$ It's an upper triangular matrix .QR There are three common methods of decomposition ：Givens Transformation 、Householder Transformation , as well as Gram-Schmidt Orthogonalization .

• HouseholderQR： No rotation （no pivoting）, Fast but unstable
• ColPivHouseholderQR： Column rotation （column pivoting）, Slower but more accurate
• FullPivHouseholderQR： Full rotation （full pivoting）, Slow speed , Most stable

The following code cannot compare speed and accuracy , Because the matrix is too small .

2.1 HouseholderQR

HouseholderQR Decomposition is 3 Kind of QR The fastest kind of decomposition , But the accuracy is the lowest .

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main()
{
    
   Matrix3f A;
   Vector3f b;
   A << 1,2,3,  4,5,6,  7,8,10;
   b << 3, 3, 4;

    struct timeval start, end;
    gettimeofday(&start, NULL);

   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   Vector3f x = A.householderQr().solve(b);
   cout << "The solution is:\n" << x << endl;

   gettimeofday(&end, NULL);
   int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
   printf(" The calculation of linear equations takes time : %d us\n", timeuse);
}

Output ：

Here is the matrix A:
 1  2  3
 4  5  6
 7  8 10
Here is the vector b:
3
3
4
The solution is:
      -2
0.999998
       1
 The calculation of linear equations takes time :  480  us

2.2 ColPivHouseholderQR

ColPivHouseholderQR Speed and accuracy are at 3 Intermediate states in the decomposition method , It's a good compromise .

• The code for

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main()
{
    
   Matrix3f A;
   Vector3f b;
   A << 1,2,3,  4,5,6,  7,8,10;
   b << 3, 3, 4;

    struct timeval start, end;
    gettimeofday(&start, NULL);

   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   Vector3f x = A.colPivHouseholderQr().solve(b);
   cout << "The solution is:\n" << x << endl;

   gettimeofday(&end, NULL);
   int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
   printf(" The calculation of linear equations takes time : %d us\n", timeuse);
}

Output ：

Here is the matrix A:
 1  2  3
 4  5  6
 7  8 10
Here is the vector b:
3
3
4
The solution is:
      -2
0.999997
       1
 The calculation of linear equations takes time :  482  us

2.3 FullPivHouseholderQR

FullPivHouseholderQR Decomposition is 3 individual QR The one with the highest accuracy in decomposition , But its speed is also the slowest .

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main()
{
    
   Matrix3f A;
   Vector3f b;
   A << 1,2,3,  4,5,6,  7,8,10;
   b << 3, 3, 4;

    struct timeval start, end;
    gettimeofday(&start, NULL);

   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   Vector3f x = A.fullPivHouseholderQr().solve(b);
   cout << "The solution is:\n" << x << endl;

   gettimeofday(&end, NULL);
   int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
   printf(" The calculation of linear equations takes time : %d us\n", timeuse);
}

Output ：

Here is the matrix A:
 1  2  3
 4  5  6
 7  8 10
Here is the vector b:
3
3
4
The solution is:
      -2
       1
0.999999
 The calculation of linear equations takes time :  131  us

3. LLT decompose

LLT Decomposition requires coefficient matrix A It's a positive definite matrix (Positive definite matrix), It is the fastest of all decomposition methods . When used for the decomposition of non positive definite matrix , It is difficult to get the right result .

LLT Decomposition is matrix Cholesky decompose , Also known as square root decomposition , yes LDLT A special form of decomposition , That is, one of them D Is the unit matrix . Symmetric positive definite matrices A It can be decomposed into a lower triangular matrix L and L The transpose LT The form of multiplication ：
$$A=L{L}^T=R^{T}R$$
Among them L It's a lower triangular matrix ,R It's an upper triangular matrix .

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main()
{
    
   Matrix3f A;
   Vector3f b;
   A << 1,2,3,  4,5,6,  7,8,10;
   b << 3, 3, 4;

    struct timeval start, end;
    gettimeofday(&start, NULL);

   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   Vector3f x = A.llt().solve(b);
   cout << "The solution is:\n" << x << endl;

   gettimeofday(&end, NULL);
   int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
   printf(" The calculation of linear equations takes time : %d us\n", timeuse);
}

Output ：

Here is the matrix A:
 1  2  3
 4  5  6
 7  8 10
Here is the vector b:
3
3
4
The solution is:
 4.4556
-0.3184
 -0.026
 The calculation of linear equations takes time :  97  us

4. LDLT decompose

LDLT Decomposition requires coefficient matrix A It's a positive definite matrix (positive definite matrix) Or semi negative definite matrix (negative semi-definite matrix). When used for the decomposition of other matrices , It is difficult to get the right result .

A Is symmetric matrix , And any one K The principal submatrix of order is not 0 when ,A There are the following unique decomposition forms ：

namely L Is the lower triangular identity matrix ,D It's a diagonal matrix .LDLT The method is actually Cholesky Improvement of decomposition method （LLT Decomposition requires square ）, For solving linear equations .

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main()
{
    
   Matrix3f A;
   Vector3f b;
   A << 1,2,3,  4,5,6,  7,8,10;
   b << 3, 3, 4;

    struct timeval start, end;
    gettimeofday(&start, NULL);

   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   Vector3f x = A.ldlt().solve(b);
   cout << "The solution is:\n" << x << endl;

   gettimeofday(&end, NULL);
   int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
   printf(" The calculation of linear equations takes time : %d us\n", timeuse);
}

Output ：

Here is the matrix A:
 1  2  3
 4  5  6
 7  8 10
Here is the vector b:
3
3
4
The solution is:
 4.4556
-0.3184
 -0.026
 The calculation of linear equations takes time :  100  us

5. LU decompose

LU decompose (LU Decomposition) It is the most common kind of matrix decomposition , It is also the most classic , It can decompose a matrix into the product of a unit lower triangular matrix and an upper triangular matrix . Put the given coefficient matrix A Into two equivalent matrices L and U The product of the , among L and U They are unit lower triangular matrix and upper triangular matrix .

5.1 LU decompose

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main()
{
    
   Matrix3f A;
   Vector3f b;
   A << 1,2,3,  4,5,6,  7,8,10;
   b << 3, 3, 4;

    struct timeval start, end;
    gettimeofday(&start, NULL);

   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   Vector3f x = A.lu().solve(b);
   cout << "The solution is:\n" << x << endl;

   gettimeofday(&end, NULL);
   int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
   printf(" The calculation of linear equations takes time : %d us\n", timeuse);
}

Output

Here is the matrix A:
 1  2  3
 4  5  6
 7  8 10
Here is the vector b:
3
3
4
The solution is:
      -2
       1
0.999999
 The calculation of linear equations takes time :  200  us

5.2 partialPivLu

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main()
{
    
   Matrix3f A;
   Vector3f b;
   A << 1,2,3,  4,5,6,  7,8,10;
   b << 3, 3, 4;

    struct timeval start, end;
    gettimeofday(&start, NULL);

   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   Vector3f x = A.partialPivLu().solve(b);
   cout << "The solution is:\n" << x << endl;

   gettimeofday(&end, NULL);
   int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
   printf(" The calculation of linear equations takes time : %d us\n", timeuse);
}

Output ：

Here is the matrix A:
 1  2  3
 4  5  6
 7  8 10
Here is the vector b:
3
3
4
The solution is:
      -2
       1
0.999999
 The calculation of linear equations takes time :  390  us

5.3 fullPivLu

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main()
{
    
   Matrix3f A;
   Vector3f b;
   A << 1,2,3,  4,5,6,  7,8,10;
   b << 3, 3, 4;

    struct timeval start, end;
    gettimeofday(&start, NULL);

   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   Vector3f x = A.fullPivLu().solve(b);
   cout << "The solution is:\n" << x << endl;

   gettimeofday(&end, NULL);
   int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
   printf(" The calculation of linear equations takes time : %d us\n", timeuse);
}

Output ：

Here is the matrix A:
 1  2  3
 4  5  6
 7  8 10
Here is the vector b:
3
3
4
The solution is:
      -2
0.999998
       1
 The calculation of linear equations takes time :  397  us

6. SVD decompose

Singular value decomposition (Singular Value Decomposition, hereinafter referred to as SVD) It is a widely used algorithm in the field of machine learning , It can not only be used for feature decomposition in dimensionality reduction algorithms , It can also be used in recommendation systems , And natural language processing . Is the cornerstone of many machine learning algorithms .SVD It's also a decomposition of the matrix , But unlike feature decomposition ,SVD The matrix to be decomposed is not required to be a square matrix . Suppose our matrix A It's a m×n Matrix , So let's define the matrix A Of SVD by ：
$$A=UD{V}^T=\left(\begin{array}{cc}\Sigma & 0\\ 0& 0\end{array}\right)$$
among ,$U$ by $m\times m$ Matrix ,$\Sigma$ by $m\times n$ Matrix ,$V$ by $n\times n$ Matrix .$\Sigma =diag({\sigma }_1,{\sigma }_2,...,{\sigma }_r)$,$\sigma$ For matrix A All nonzero singular values of .$U$ and $V$ Satisfy ,$U^{T}U=I,V^{T}V=I$

When the number of equations is greater than the number of unknowns , The least square solution is required , The most effective way is to SVD decompose ,Eigen Two decomposition methods are provided , Namely BDCSVD and JacobiSVD. Generally, it is recommended to use BDCSVD, It can well expand large matrices , For smaller matrices , It will automatically return to JacobiSVD class .

Be careful ： use SVD When it breaks down , Use Dynamic matrix Define coefficient matrix A、 Constant matrix b、 Matrix of unknowns x.

6.1 BDCSVD decompose

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main()
{
    
	MatrixXd A(3,2);	// coefficient matrix A,3×2 rank 
	VectorXd b(3,1);	// Constant matrix b,3×1 rank 
	VectorXd x(3,1);	// Matrix of unknowns x,3×1 rank 

   A << 1, 2, 4, 5, 7, 8;
   b << 3, 3, 4;

   struct timeval start, end;
   gettimeofday(&start, NULL);

   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   x = A.bdcSvd(ComputeThinU | ComputeThinV).solve(b);
   cout << "The solution is:\n" << x << endl;

   gettimeofday(&end, NULL);
   int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
   printf(" The calculation of linear equations takes time : %d us\n", timeuse);
}

Output ：

Here is the matrix A:
1 2
4 5
7 8
Here is the vector b:
3
3
4
The solution is:
   -2.5
2.66667
 The calculation of linear equations takes time :  675  us

6.2 JacobiSVD decompose

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main()
{
    
	MatrixXd A(3,2);	// coefficient matrix A,3×2 rank 
	VectorXd b(3,1);	// Constant matrix b,3×1 rank 
	VectorXd x(3,1);	// Matrix of unknowns x,3×1 rank 
	A << 1, 2,  4, 5,  7, 8;
	b << 3, 3, 4;

    struct timeval start, end;
    gettimeofday(&start, NULL);

   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   x = A.jacobiSvd(ComputeThinU | ComputeThinV).solve(b);
   cout << "The solution is:\n" << x << endl;

   gettimeofday(&end, NULL);
   int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
   printf(" The calculation of linear equations takes time : %d us\n", timeuse);
}

Output ：

Here is the matrix A:
1 2
4 5
7 8
Here is the vector b:
3
3
4
The solution is:
   -2.5
2.66667
 The calculation of linear equations takes time :  578  us

7. Inverse matrix method

Eigen It also provides an algorithm for finding the inverse matrix and the determinant of the matrix , But these two algorithms are very uneconomical algorithms for large matrices , When you need to do this kind of operation on a large matrix , You need to judge whether you need to do this . But for small matrices Can be used without concern .

#include <iostream>
#include<sys/time.h>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main()
{
    
    Matrix3d A; // coefficient matrix A
    Vector3d b; // Constant matrix b
    Vector3d x; // Matrix of unknowns x
    A << 1, 2, 3, 4, 5, 6, 7, 8, 10;
    b << 3, 3, 4;
    cout << " coefficient matrix A:\n"
         << A << endl;
    cout << " Constant matrix b:\n"
         << b << endl;

    struct timeval start, end;
    gettimeofday(&start, NULL);
    if (A.determinant() != 0)
    {
    
        // The matrix determinant is greater than 0,
        x = A.inverse() * b;
        cout << " Matrix of unknowns x:\n"
             << x << endl;
    }
    else
    {
    
        cout << " The matrix determinant is less than 0, Matrix equation has no solution ！\a\n"
             << endl;
    }

    gettimeofday(&end, NULL);
    int timeuse = 1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec;
    printf(" The calculation of linear equations takes time : %d us\n", timeuse);
    return 0;
}

Output ：

 coefficient matrix A:
 1  2  3
 4  5  6
 7  8 10
 Constant matrix b:
3
3
4
 Matrix of unknowns x:
-2
 1
 1
 The calculation of linear equations takes time :  63  us

---

Reference documents ：
https://eigen.tuxfamily.org/dox/group__TutorialLinearAlgebra.html
https://blog.csdn.net/qq_41839222/article/details/96274251