Animation_ IK overview

0. Write it at the front

This article is a collection of personal learning notes , If there is a mistake , I hope you can point out .

1. TwoBoneIK

Limit IK The bone chain of can only have 2 Root bone and a joint （2 Not available above root ）, Under such restrictions , Geometry （TwoBoneIK） Is the best solution .
Solver goals ： Calculate the angle of each joint through the cosine theorem
1. Derivation process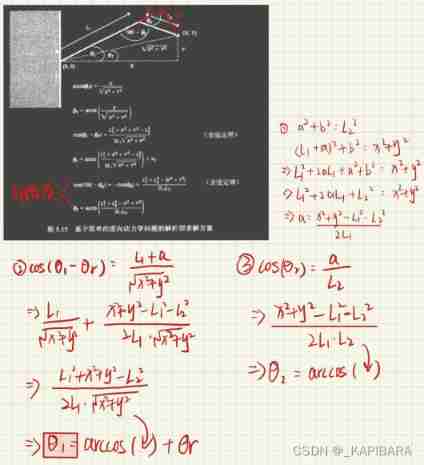

2. Exclude the situation that the target cannot be reached
|L1-L2|≤LT≤L1+L2
among L1 and L2 Is the length of two bones ,LT yes Target To Base Distance of
The two distances must satisfy the above inequality

3. Feasible solution is not unique

A two-dimensional ： Two solutions can be found , And it is symmetrical with respect to the vector pointing to the target position of the starting joint point . You can exclude an illegal solution by constraining the rotation angle of the joint .
The three dimensional ： In order to （ The vector from the starting joint point to the target position ） Is the feasible solution on the specific circle of the axis , There are countless solutions .UE4 Is to specify a reference plane through the outside , To determine a unique solution .

4.UE4 Of TwoBoneIK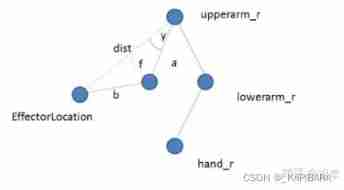

（ The picture is quoted from references [1]）

• Effector Location: designated Target Location
• DistDir： Point from the starting position Target Vector of position , And you can get the length directly dist
• Joint Target Location： A vertex of external input , Is the key , It is used to fix the parameters of one solution among countless solutions in three-dimensional space .
• JointBlendDir： be located Joint Target Location（ Specify a point ）,RootPos（ Joint starting point ） and EffectorLocation（ Destination ） A plane composed of three points , And perpendicular to DistDir Unit vector .

Because the end position and start position are fixed , Just ask for the position of the middle joint

cos(y) = (a^2 + dist^2 - b^2) / (2 * a * dist);         				===>>  Cosine theorem finds the rotation angle of the first joint , That is to say cos（θ1-θr）
f = a * sin(y);                                                         ===>>  seek f The length of , Used to calculate the projection distance later 
ProjDist = FMath::Sqrt(a^2 - f^2);                        				===>>  Pythagorean theorem a stay DistDir Projection distance on 
OutJointPos = RootPos + (ProjDist *DistDir) + (f  * JointBlendDir);     ===>>   Finally, add the position of the starting point of the joint through the vector , Get the final required position of the middle joint .

2. FABRIK

FABRIK： Forward and backward arrival IK（Forward and Backward Reaching Inverse Kinematics）
Support multiple bones IK, But it mainly controls the position of bones , Not responsible for controlling the rotation of bones
By traversing the bone chain forward and backward, the position of the bone converges to the solution （ Maybe not the best , Determined by the number of iterations and accuracy ）

1. Solution idea

• First calculate the length of the whole bone chain , Judge whether the target point can be reached , If you can't reach , Requires the root bone to move .
• Start with the end bone , Take down the bones directly , Put the end effector in Target Target location , And both ends of this bone , And the ends of the remaining bones with Target The connecting line of should be in the same straight line .
• Remove the remaining bones in turn , And in accordance with the 1 Rules to place the removed bones .
• When 1~2 After all the steps are executed （ This is the forward traversal arrival （Forward Reaching））, To the original Target The position is the starting position of the bone chain , primary Base Set to Target Location , Re execution 1~2 Step , This is the backward traversal arrival （Backward Reaching）
• repeat 1~3 Step , Until the end effector reaches a certain threshold of the target point , Or the number of iterations （UE4 The default is 10） stop it .
  ![ Insert picture description here ](https://img-blog.csdnimg.cn/2ec67e9ae06b4a139b362d900ebda06e.png

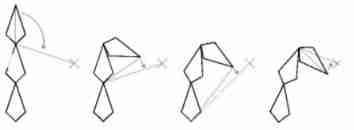
3. CCDIK

CCD：Cyclic Coordinate Descent Circular coordinate descent method
Support multiple bones IK, But the main thing is to control the bone rotation to IK The effect of , and FABRIK contrary

1. Solution idea

• Start with the first node of the bone chain near the end effector
• Find the vector that the current node points to the end effector , Point to the current node Target Included angle of vector of target position
• Apply this included angle to the rotation of the node （ If it's an intermediate node , Its child joints should also be based on this transformation ）, All the way to Root node
• Then start the cycle from the first node
  

4. Jacobia IK

TODO

5. Fullbody IK

TODO

6. Reference material

[1] https://zhuanlan.zhihu.com/p/41425611
[2] https://blog.csdn.net/noahzuo/article/details/80188366