Topological sorting

One . What is topological sort

A topological sort （Topological Sorting） It's a directed acyclic graph （DAG, Directed Acyclic Graph） The linear sequence of all vertices of . And the sequence must satisfy the following two conditions ： Every vertex appears and only once . If there is one from the top A To the top B The path of , So the vertices in the sequence A Appear at the top B In front of .

Two . Picture description

The problem solved by this algorithm is similar to the process of handling affairs
One or more related things that must be done before doing one thing

3、 ... and . Code implementation diagram

1. First of all, find the tasks that do not need other tasks to pave the way , Points in the picture 1. take 1 Join the team first , Look for other points , After the first search , Start to get out of the team , take 1 Out of the team , Look for tasks related to him , A condition for unlocking subsequent tasks .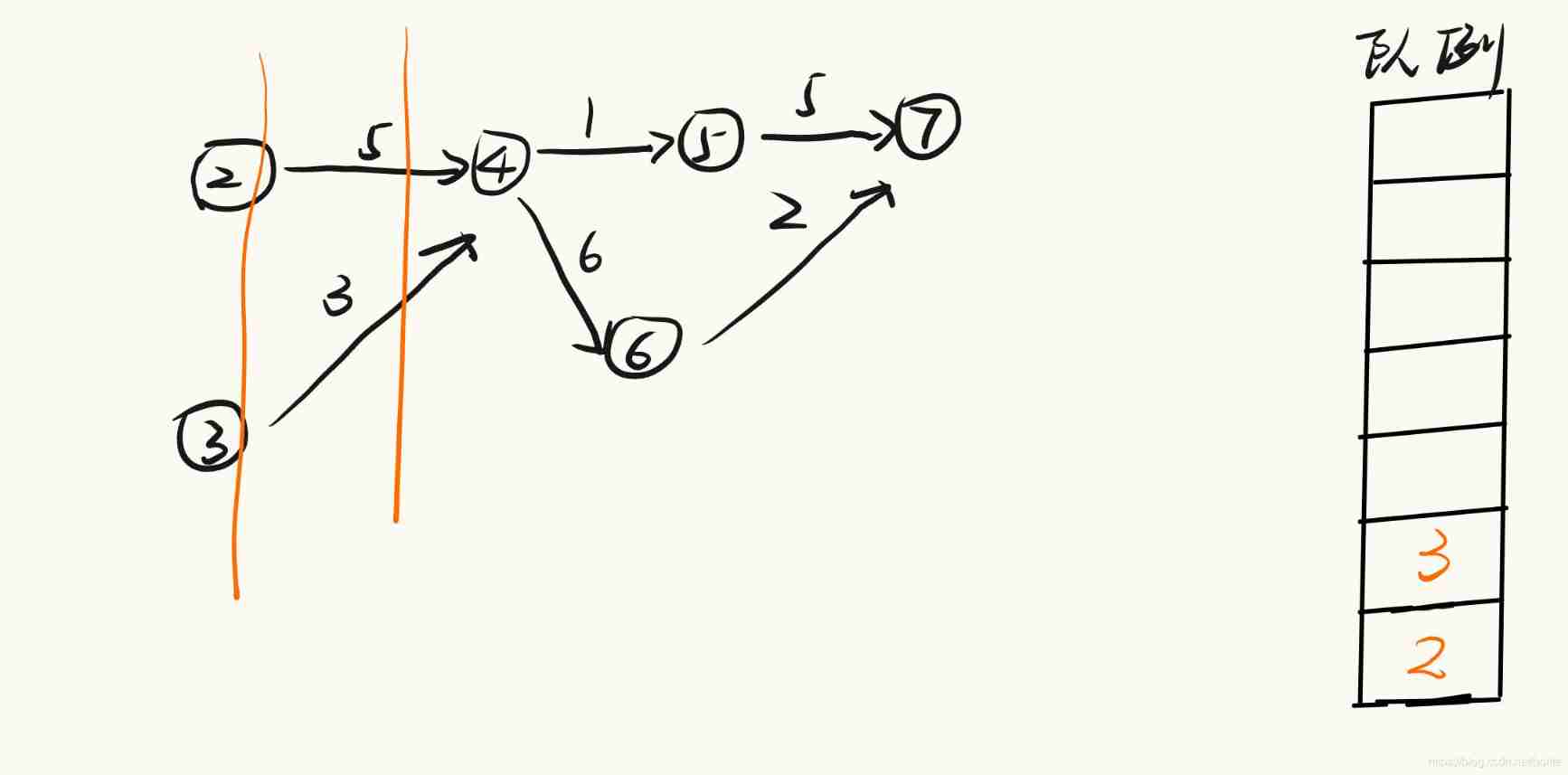

Once again, the task that looks for the current fully unlocked condition will join the team again , In turn, cycle , Until the team is empty

Four . Related examples

1. 6-5- A topological sort The rationality of task scheduling (25 branch )

Suppose an engineering project consists of a set of subtasks , Some of the subtasks can be executed in parallel , Some can only be executed after completing other subtasks .“ Task scheduling ” Includes a set of subtasks 、 And the set of subtasks on which each subtask can execute .

For example, completing all courses and graduation design of a major can be regarded as a project to be completed by an undergraduate , Each course can be regarded as a sub task . Some courses can be offered at the same time , Such as English and C Programming , They don't have to fix which door first ; Some courses cannot be offered at the same time , Because they have sequential dependencies , such as C Programming and data structure , We must learn the former first .

But here's the thing , For a set of subtasks , Not any task scheduling is a feasible scheme . For example, there are “ The subtasks A Dependent on subtasks B, The subtasks B Dependent on subtasks C, The subtasks C And depends on subtasks A”, Then none of these three tasks can be performed first , This is an infeasible solution . Your job now is to write a program to determine whether any given task scheduling is feasible .

Input format :
Enter description ： Enter the first line to give the number of subtasks N（≤100）, Subtasks by 1~N Number . And then N That's ok , Each row gives a dependent set of subtasks ： First, the number of subtasks in the dependent set is given K, Subsequently given K Subtask number , Integers are separated by spaces .

Output format :
If the scheme is feasible , The output 1, Otherwise output 0.

sample input 1:

12
0
0
2 1 2
0
1 4
1 5
2 3 6
1 3
2 7 8
1 7
1 10
1 7

sample output 1:

1

sample input 2:

5
1 4
2 1 4
2 2 5
1 3
0

sample output 2:

0

#include<iostream>
#include<queue>
using namespace std;
#define N 120
int main()
{
    
	int a[N][N] = {
     0 };
	int size[N] = {
     0 };
	queue<int>q;// Build a team to save unlocked tasks 
	int n;
	cin >> n;
	int i = 0;
	int m;
	int aim;
	for (i = 1; i <= n; i++) {
    
		cin >> m;
		for (int j = 0; j < m; j++) {
    
			cin >> aim;
			a[i][aim] = 1;// Link the task to the unlock condition 
			size[i]++;// Record the number of unlocked conditions , When the number is 0 Unlock when 
		}
	}
	for (i = 1; i <= n; i++) {
    
		if (!size[i]) {
    
			q.push(i);// Look for unconditional tasks for the first time 
		}
	}
	while (!q.empty()) {
    
		aim = q.front();
		q.pop();
		for (i = 1; i <= n; i++) {
    // Find the task that needs this task as the unlocking condition 
			if (a[i][aim]) {
    
				size[i]--;// The number of a condition that cancels the task 
				if(!size[i]) q.push(i);// If the task reaches unlock , Join the team 
			}
		}
	}
	for (i = 1; i <= n; i++) {
    
		if (size[i] != 0) {
    
			cout << "0";
			return 0;
		}
	}
	cout << "1" << endl;
}

2. 7-99 Minimum working period (25 branch )

A project consists of several tasks , There is sequence dependence between tasks . The project manager needs to set a series of milestones , Check the completion of the task at each milestone node , And start the following tasks . Given the relationship between tasks in a project , Please calculate the earliest completion time of this project .

Input format ：
First, the first line gives two positive integers ： Number of project milestones N（≤100） And the total number of tasks M. The milestones here are from 0 To N−1 Number . And then M That's ok , Each line gives a description of the task , The format is “ Task start milestone Task end milestone Working hours ”, All three numbers are non negative integers , Space off .

Output format ：
If the arrangement of the whole project is reasonable and feasible , Output the earliest completion time in one line ; Otherwise output "Impossible".

sample input 1：

9 12
0 1 6
0 2 4
0 3 5
1 4 1
2 4 1
3 5 2
5 4 0
4 6 9
4 7 7
5 7 4
6 8 2
7 8 4

sample output 1：

18

sample input 2：

4 5
0 1 1
0 2 2
2 1 3
1 3 4
3 2 5

sample output 2：

Impossible

#include<iostream>
#include<queue>
using namespace std;
#define N 120
int main()
{
    
	int map[N][N];
	int cost[N] = {
     0 };
	int size[N] = {
     0 };
	queue<int> q;
	int n, m;
	cin >> n >> m;
	int i = 0;
	int j = 0;
	for (i = 0; i < n; i++) {
    
		for (j = 0; j < n; j++) {
    
			map[i][j] = -1;// Because the duration is 0 The situation of , So the initial words are -1
		}
	}
	int a1, a2, w;
	for (i = 0; i < m; i++) {
    
		cin >> a1 >> a2 >> w;
		map[a1][a2] = w;
		size[a2]++;
	}
	int aim;
	int sum = 0;
	for (i = 0; i < n; i++) {
    
		if (!size[i]) q.push(i);
	}
	while (!q.empty()) {
    
		aim = q.front();
		q.pop();
		if (cost[aim] > sum)sum = cost[aim];
		for (i = 0; i < n; i++) {
    
			if (map[aim][i] != -1) {
    
				size[i]--;
				if (!size[i])q.push(i);
				if (cost[i] < cost[aim] + map[aim][i])
					cost[i] = cost[aim] + map[aim][i];// Refresh the duration of the current node 
			}
		}
	}
	for (i = 0; i < n; i++) {
    
		if (size[i]) {
    
			cout << "Impossible" << endl;
			return 0;
		}
	}
	cout << sum << endl;
}

5、 ... and . Key code

	for (i = 1; i <= n; i++) {
    
		if (!size[i]) {
    
			q.push(i);// Look for unconditional tasks for the first time 
		}
	}
	while (!q.empty()) {
    
		aim = q.front();
		q.pop();
		for (i = 1; i <= n; i++) {
    // Find the task that needs this task as the unlocking condition 
			if (a[i][aim]) {
    
				size[i]--;// The number of a condition that cancels the task 
				if(!size[i]) q.push(i);// If the task reaches unlock , Join the team 
			}
		}
	}

This code can achieve the effect of topological sorting , And some problems need the expansion of the code