当前位置:网站首页>线性代数期末复习存档
线性代数期末复习存档
2022-08-02 14:03:00 【宇 -Yu】
1.实对称矩阵的定义
n阶矩阵A,其矩阵的元素都为实数,且矩阵A的转置等于其本身(aij=aji)则称A为实对称矩阵。

1.实对称矩阵A的不同特征值对应的特征向量是正交的。
3.n阶实对称矩阵A必可对角化,且相似对角阵上的元素即为矩阵本身特征值。
4.若λ0具有k重特征值 必有k个线性无关的特征向量,或者说必有秩r(λ0E-A)=n-k,其中E为单位矩阵。
2.齐次方程的解
1,写出系数矩阵A
;2,通过行的初等变换化A为标准形;3,判别解的情况,只有零解还是有非零解;4,写出基础解系及全部解。
标准形首先它是阶梯形,然后还要满足两个条件:1.非零行首个非零元素均为1;
2,这些“1”所在列其它元素均为零。
当一个齐次线性方程组有无穷多解时,每一个解就是一个n维解向量,这无穷多个解向量构成了一个向量空间(称为解向量空间)。
3.线性相关,线性无关
4.初等变換
矩阵的初等行变换和初等列变换统称为初等变换。另外:分块矩阵也可以定义初等变换。
定义:如果B可以由A经过一系列初等变换得到,则称矩阵A与B称为等价
所谓数域P上矩阵的初等行变换是指下列3种变换:
1)以P中一个非零的数乘矩阵的某一行
2)把矩阵的某一行的c倍加到另一行,这里c是P中的任意一个数
3)互换矩阵中两行的位置
5.正交矩阵的定义。
各列向量之间分别正交(内积为0)
各列向量,都是单位向量
|A|=1或-1
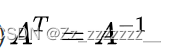
二.选择题5个
1.特征值与特征向量
2.行列式的若干性质
3.两个矩阵相似的定义,性质
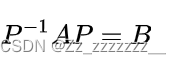
1、反身性:任何矩阵都与它本身相似。
2、对称性:如果 A和 B相似,那么 B就和 A相似。
3、传递性:如果 A和 B相似, B和 C相似,那么 A也和 C相似。
A可对角化即
A具有 n个线性无关的特征向量。

矩阵特征向量的几何含义
矩阵乘以一个向量的结果仍是同维数的一个向量。
注意:特征向量不能是零向量)。
综上所述,一个变换(或者说矩阵)的特征向量就是这样一种向量,它经过这种特定的变换后保持方向不变,只是进行长度上的伸缩而已。
4.伴随矩阵的定义,性质

注意
原来矩阵按行展开,你就按列写。列展开你就按行写。因为他有一个转置。
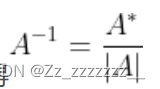
https://blog.csdn.net/rgbhi/article/details/123286265
5.非齐次线性方程组的解(什么时候有解,无
解,有无穷解)
非齐次线性方程组(Nonhomogeneous linear equations),是指常数项不全为零的线性方程组,
表达式为Ax=b。 线性方程组在什么时候有唯一解/无穷个解/无解? - 知乎
线性方程组在什么时候有唯一解/无穷个解/无解? - 知乎
三.填空题5个
1.齐次线性方程组有非零解的条件
n元齐次线性方程组有非零解的充要条件是其系数行列式为零。
等价地,方程组有唯一的零解的充要条件是系数矩阵不为零。
齐次方程组有非零解的判定
- 发给给给给给给给给gggggggggggggggggggSS
2.线性相关的定义
向量组只包含一个向量a时,a为0向量,则说A线性相关;
若a≠0, 则说A线性无关。
包含零向量的任何向量组是线性相关的。
3.矩阵乘积的行列式性质
4相似矩阵之间的性质,逆,原矩阵特征值有关
的性质
5.特征值的定义
三计算题
 1线性表出定义(给几个具体向量,进行表出)
1线性表出定义(给几个具体向量,进行表出)
2.给出一个三阶方阵求转置,逆,余子式,代数
余子式,伴随矩阵
3.求齐次线性方程组的通解(含四个末知量)
4将一个二元的二次型化成标准型(用正交变换
法)
d28
5.求矩阵的特征值,特征向量及判断是否可以相
似对角化
相似对角化的条件是:
n阶方阵存在n个线性无关的特征向量;
如果这个n阶方阵有n个不同的特征值,那么矩阵必然存在相似矩阵;
如果阶n方阵存在重复的特征值,每个特征值的线性无关的特征向量的个数恰好等于该特征值的重复次数。
对称矩阵(Symmetric Matrices)是指以主对角线为对称轴,各元素对应相等的矩阵。 [1] 在线性代数中,对称矩阵是一个方形矩阵,其转置矩阵和自身相等。
边栏推荐
猜你喜欢
随机推荐
[ROS]ROS常用工具介绍(待续)
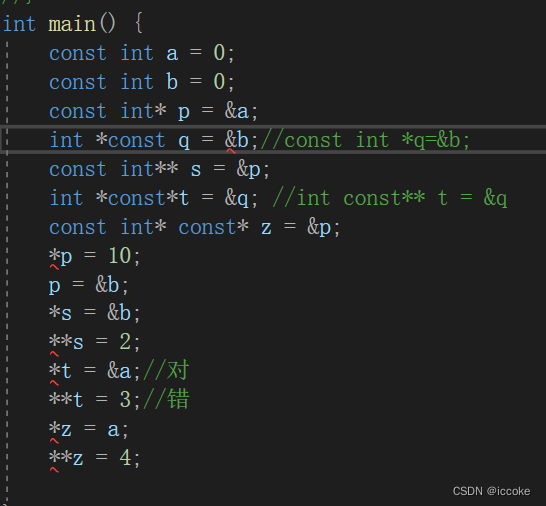
C语言——一级指针初识
Paddle window10 environment using conda installation
STM32 (F407) - stack
动手学ocr(一)
字符串的小知识
【ROS】编译软件包packages遇到进度缓慢或卡死,使用swap
关于密码加密的一点思路
Basic operations of 8583 sequential stack
drf源码分析与全局捕获异常
Creating seven NiuYun Flask project complete and let cloud
drf序列化器-Serializer
chapter7
【ROS】工控机的软件包不编译
redis delay queue
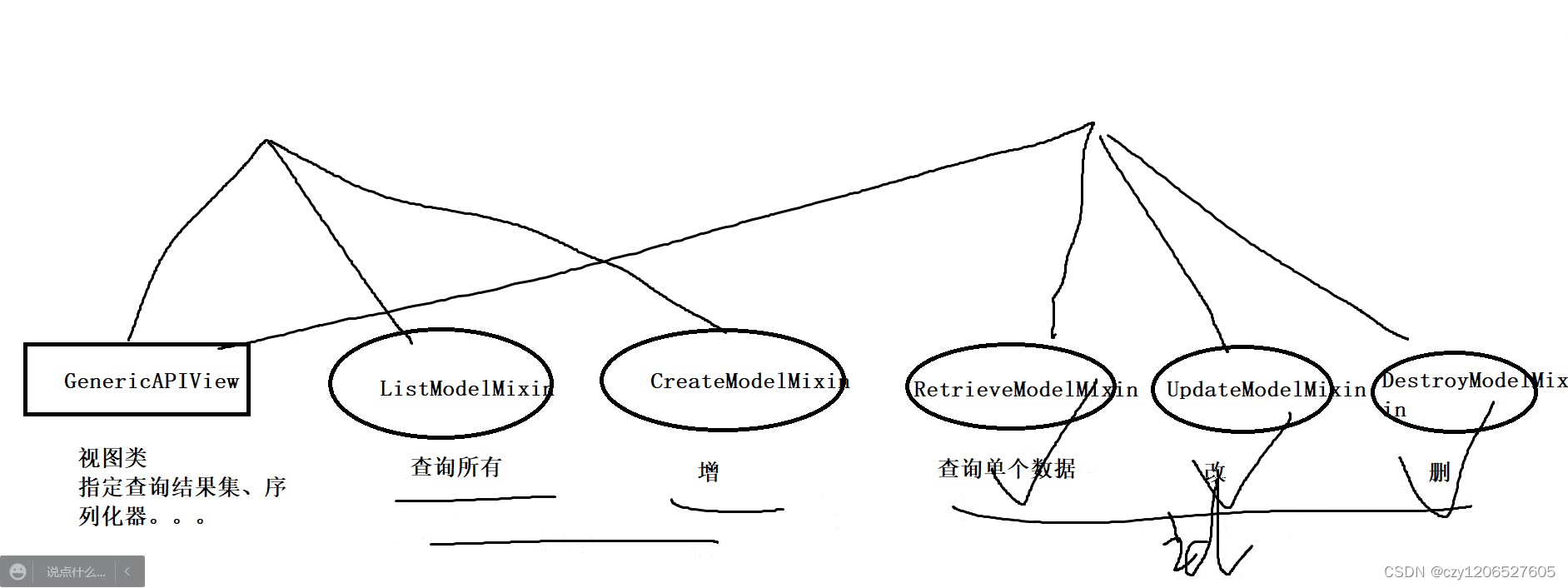
第十四单元 视图集及路由
[ROS] The software package of the industrial computer does not compile
IDEA打包jar包
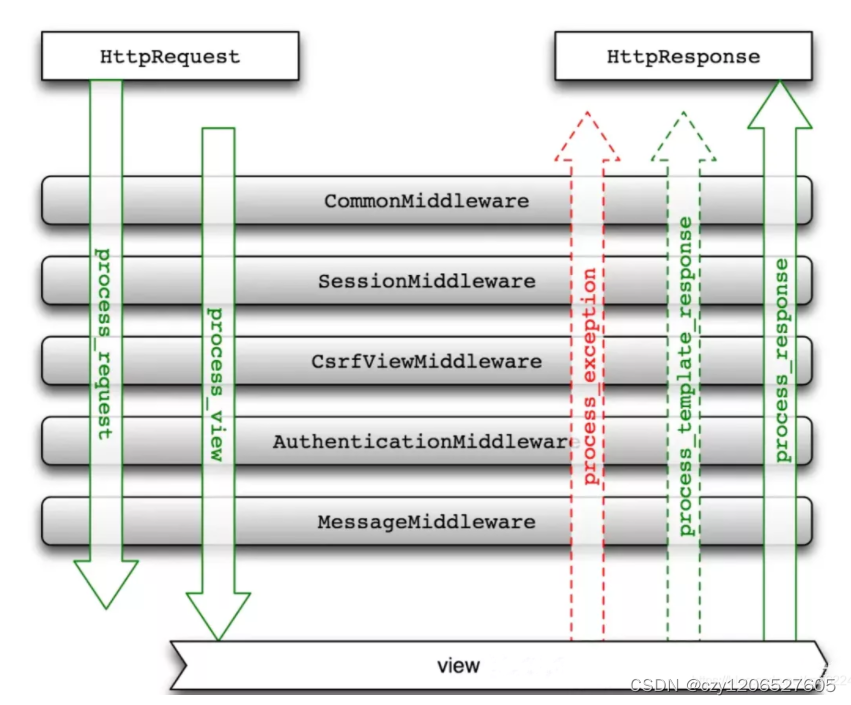
Unit 8 Middleware
C语言初级—从键盘接收一个整形并逆序输出
![[ROS] (02) Create & compile ROS package Package](/img/c2/5931d5cbade509c6ca34d66a274756.png)